《算法竞赛进阶指南》之贪心篇（防晒+畜栏预定+雷达设备+国王游戏）

关于无聊的瞎唠嗑
看算法基础课的时候，Y总啊称贪心为最难的算法，我听了听寻思，这感觉还好啊、、、凭感觉做可以的！
奈何翻开书被现实毒打，孩子还太天真了，贪心永远不难在它怎么做的，你运气好猜对了那是非常好，运气不好猜错了，那是真的不知道错在哪啊。
总结一下，贪心凭感觉，证明靠天赋。接下来就看看贪心的题目，到底有，多难。。。

防晒

原题链接：

https://www.acwing.com/problem/content/112/

题目大意：
有 C 头奶牛进行日光浴，第 i 头奶牛需要 minSPF[i] 到 maxSPF[i] 单位强度之间的阳光。

每头奶牛在日光浴前必须涂防晒霜，防晒霜有 L 种，涂上第 i 种之后，身体接收到的阳光强度就会稳定为 SPF[i]，第 i 种防晒霜有 cover[i] 瓶。

求最多可以满足多少头奶牛进行日光浴。

输入格式
第一行输入整数 C 和 L。

接下来的 C 行，按次序每行输入一头牛的 minSPF 和 maxSPF 值，即第 i 行输入 minSPF[i] 和 maxSPF[i]。

再接下来的 L 行，按次序每行输入一种防晒霜的 SPF 和 cover 值，即第 i 行输入 SPF[i] 和 cover[i]。

每行的数据之间用空格隔开。

输出格式
输出一个整数，代表最多可以满足奶牛日光浴的奶牛数目。

数据范围
1≤C,L≤2500,
1≤minSPF≤maxSPF≤1000,
1≤SPF≤1000

输入样例：
3 2
3 10
2 5
1 5
6 2
4 1
输出样例：
2

题目意思

就是说给你c个区间和l个数，问你这l个数最多可以包含在多少个区间内

解题思路

首先，凭感觉。以区间的左端点从小到大排序，然后将L给点也从小到大排序，如果点在区间内，则ans++;
然后，开始测试!
WA了…
于是，这是为什么呢?
我们来证明一下自己的做法。首先对于点，x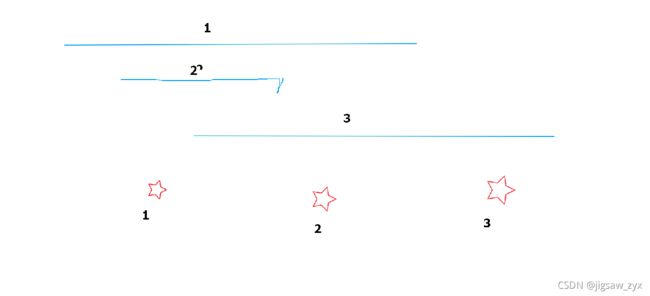 然后对于区间min[i]
自己话的有点丑啊哈哈哈，将就看了。
红色星星代表点，蓝色代表区间了，我们可以看见如果依照我们刚才的思路的话，原本三个星星都可以对应一个蓝色区间，我们的做法就只能两个星星对应了。
那么，怎么提高呢?
既然我们从左端点从小到大不行，那么右端点呢？
如果从右端点从小到大排序，那这种情况就迎刃而解了，那么，开始敲代码！

AC代码

#include
#include
using namespace std;

struct sp{
    int minn,maxx;
    bool A=0;
}spf[2510];

struct sp2{
    int spfi,cover;
}spff[2510];

bool cmp1(sp x,sp y){
    if(x.maxx!=y.maxx) return x.maxx<y.maxx;
    else return x.minn<y.minn;
}

bool cmp2(sp2 x,sp2 y){
    if(x.spfi!=y.spfi) return x.spfi<y.spfi;
    else return x.cover<y.cover;
}

int main(){
   int c,l;
   cin>>c>>l;
   
   for(int i=0;i<c;i++){
       cin>>spf[i].minn>>spf[i].maxx;
       if(spf[i].minn>spf[i].maxx) swap(spf[i].minn,spf[i].maxx);
       
   }
   sort(spf,spf+c,cmp1);
   
   for(int i=0;i<l;i++) cin>>spff[i].spfi>>spff[i].cover;
   sort(spff,spff+l,cmp2);
   
   int ans=0;
   for(int j=0;j<l;j++){
       int n=spff[j].cover;
       int m=spff[j].spfi;
      
      for(int i=0;i<c;i++){
          if(spf[i].A==1) continue;
          if(spf[i].minn<=m&&m<=spf[i].maxx){ans++;n--;spf[i].A=1;}
          if(n==0) break;
         // if(spf[i].minn>m) break;
      }
   }
   
 cout<<ans;
 return 0;   
}

---

畜栏预定

接下来是第二题！

原题链接：

https://www.acwing.com/problem/content/113/

题目描述：
有 N 头牛在畜栏中吃草。

每个畜栏在同一时间段只能提供给一头牛吃草，所以可能会需要多个畜栏。

给定 N 头牛和每头牛开始吃草的时间 A 以及结束吃草的时间 B，每头牛在 [A,B] 这一时间段内都会一直吃草。

当两头牛的吃草区间存在交集时（包括端点），这两头牛不能被安排在同一个畜栏吃草。

求需要的最小畜栏数目和每头牛对应的畜栏方案。

输入格式
第 1 行：输入一个整数 N。

第 2…N+1 行：第 i+1 行输入第 i 头牛的开始吃草时间 A 以及结束吃草时间 B，数之间用空格隔开。

输出格式
第 1 行：输入一个整数，代表所需最小畜栏数。

第 2…N+1 行：第 i+1 行输入第 i 头牛被安排到的畜栏编号，编号是从 1 开始的 连续 整数，只要方案合法即可。

数据范围
1≤N≤50000,
1≤A,B≤1000000

输入样例：
5
1 10
2 4
3 6
5 8
4 7
输出样例：
4
1
2
3
2
4

题目大意

我们有N个区间，我们把所有没有相交的区间划为一组，最少可以划分几组？

解题思路

将所有区间从小到大排序，然后依次遍历，如果当前区间于之前的区间相交，则新开一个组。如果不相交，则把这个区间加到之前的区间里去，然后更新区间的末尾值，这里需要优先队列来维护我们的最小堆

AC代码

#include
#include
#include
#include
#include
using namespace std;

typedef pair<int,int> PII;
const int N=50550;
pair<PII,int> cows[N];
int ans[N];

int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>cows[i].first.first>>cows[i].first.second;
        cows[i].second=i;
    }
    
    sort(cows,cows+n);
    priority_queue<PII,vector<PII>,greater<PII> > head;
    //greater从小到大排序，less从大到小排序
    
    for(int i=0;i<n;i++){
        auto cow=cows[i].first;
        if(head.empty()||head.top().first>=cow.first){
            PII stall={cow.second,head.size()+1};
            head.push(stall);
            ans[cows[i].second]=stall.second;
        }else{
            auto stall=head.top();
            head.pop();
            stall.first=cow.second;
            ans[cows[i].second]=stall.second;
            head.push(stall);
        }
    }
    
    cout<<head.size()<<endl;
    for(int i=0;i<n;i++) cout<<ans[i]<<endl;
    return 0;
}

这里的难点，其实就是对priority_queue的一系列操作，做了这道题我也学会了一些有意思的写法。

---

继续肝！

雷达设备

原题链接：

https://www.acwing.com/problem/content/114/

题目描述
假设海岸是一条无限长的直线，陆地位于海岸的一侧，海洋位于另外一侧。

每个小岛都位于海洋一侧的某个点上。

雷达装置均位于海岸线上，且雷达的监测范围为 d，当小岛与某雷达的距离不超过 d 时，该小岛可以被雷达覆盖。

我们使用笛卡尔坐标系，定义海岸线为 x 轴，海的一侧在 x 轴上方，陆地一侧在 x 轴下方。

现在给出每个小岛的具体坐标以及雷达的检测范围，请你求出能够使所有小岛都被雷达覆盖所需的最小雷达数目。

输入格式
第一行输入两个整数 n 和 d，分别代表小岛数目和雷达检测范围。

接下来 n 行，每行输入两个整数，分别代表小岛的 x，y 轴坐标。

同一行数据之间用空格隔开。

输出格式
输出一个整数，代表所需的最小雷达数目，若没有解决方案则所需数目输出 −1。

数据范围
1≤n≤1000,
−1000≤x,y≤1000

输入样例：
3 2
1 2
-3 1
2 1
输出样例：
2

题目大意

在笛卡尔坐标上我们给出N个点，然后给出N个点可以扫描的范围，问你在N个点所有能过扫描的范围里，在X轴上相交的有多少？

解题思路

通过三角形定理我们可以吧每个点在X轴上形成的区间算出来，同时如果存在一个不能在X轴上形成区间的，我们就可以输出-1。然后我们按右端从小到大排序，如果后面的左端小于右端，则是重叠；如果没有，ans++，更新右端，继续遍历，

AC代码

#include
#include
#include
#include
#include
using namespace std;

typedef pair<double,double> PII;
const int N=1100;
PII ld[N];

bool cmp(PII x,PII y){
    if(x.second!=y.second) return x.second<y.second;
    else return x.first<y.first;
}

int main(){
    
    int n,d;
    cin>>n>>d;
    bool A=0;
    for(int i=0;i<n;i++){
        int a,b;
        cin>>a>>b;
        double c=sqrt(d*d-b*b);
        if(b>d) A=1;
        ld[i].first=a-c,ld[i].second=a+c;
        if(ld[i].first==0&&ld[i].second==0) ld[i].first=ld[i].second=a;
        
        //cout<
    }
    if(A==1){
        cout<<-1;
        return 0;
    }
    sort(ld,ld+n,cmp);
    
    double maxx=0;
    maxx=ld[0].second;
    int ans=1;
    for(int i=0;i<n;i++){
        if(ld[i].first>maxx){
            ans++;
            maxx=ld[i].second;
        }
        
    }
    cout<<ans;
    return 0;
}

---

再来再来肝！

国王游戏

原题链接：

https://www.acwing.com/problem/content/116/

题目描述
恰逢 H 国国庆，国王邀请 n 位大臣来玩一个有奖游戏。

首先，他让每个大臣在左、右手上面分别写下一个整数，国王自己也在左、右手上各写一个整数。

然后，让这 n 位大臣排成一排，国王站在队伍的最前面。

排好队后，所有的大臣都会获得国王奖赏的若干金币，每位大臣获得的金币数分别是:

排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数，然后向下取整得到的结果。

国王不希望某一个大臣获得特别多的奖赏，所以他想请你帮他重新安排一下队伍的顺序，使得获得奖赏最多的大臣，所获奖赏尽可能的少。

注意，国王的位置始终在队伍的最前面。

输入格式
第一行包含一个整数 n，表示大臣的人数。

第二行包含两个整数 a 和 b，之间用一个空格隔开，分别表示国王左手和右手上的整数。

接下来 n 行，每行包含两个整数 a 和 b，之间用一个空格隔开，分别表示每个大臣左手和右手上的整数。

输出格式
输出只有一行，包含一个整数，表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。

数据范围
1≤n≤1000
0

输入样例：
3
1 1
2 3
7 4
4 6
输出样例：
2

题目大意

每个人有两个点，当前人获得金币数是前面所有人所有人的左手上的数的乘积除以他自己右手上的数，然后向下取整得到的结果，问怎么排序能够使获得金币最多的人最少，另外，第一个人不参与排序

解题思路

直接将所有大臣按左右手上的数的乘积从小到大排序，得到的序列就是最优排队方案，然后遍历一次得到最大的那个数

AC代码

#include
#include
#include
#include
using namespace std;

const int N = 1100;
typedef pair<int,int> PII;
PII dc[N];

vector<int> max_vc(vector<int> a,vector<int> b){
    if(a.size()>b.size()) return a;
    else if(a.size()<b.size()) return b;
    if(vector<int>(a.rbegin(),a.rend())>vector<int>(b.rbegin(),b.rend())) return a;
    else return b;
}

vector<int> mul(vector<int> a,int b){
    vector<int> c;
    int k=0;
    for(int i=0;i<a.size();i++){
        k+=a[i]*b;
        c.push_back(k%10);
        k/=10;
    }
    while(k) c.push_back(k%10),k/=10;
    return c;
}

vector<int> dvl(vector<int> a,int b){
    vector<int> c;
    bool is_first = 0;
    for(int i=a.size()-1,t=0;i>=0;i--){
        t=t*10+a[i];
        int x=t/b;
        if(x||is_first){
            is_first = 1;
            c.push_back(x);
        }
        t%=b;
    }
    return vector<int>(c.rbegin(),c.rend());
}

void output(vector<int> a){
    for(int i=a.size()-1;i>=0;i--) cout<<a[i];
    return ;
}

int main(){
    int n;
    cin>>n;
    for(int i=0;i<=n;i++){
        int a,b;
        cin>>a>>b;
        dc[i]={a*b,a};
    }
    sort(dc+1,dc+1+n);
    
    vector<int> res(1,1);
    vector<int> ans(1,1);
    
    for(int i=0;i<=n;i++){
        if(i) res=max_vc(res,dvl(ans,dc[i].first/dc[i].second));
        ans=mul(ans,dc[i].second);
    }
    
    output(res);
    return 0;
}

---

思考和总结

贪心题目其实不外乎离不开一个排序问题。
我们首先要去做的就是去猜它怎么做，
然后对于你猜的办法进行证明
如果是错的，那么怎么改正才是正确的
怎么排序就是给个关键
经常采用的就是优先队列和pair的写法，也需要多加熟悉