【蓝桥杯】每日一题17天冲刺国赛

今日题目

金币

优秀的拆分

穿越雷区

蓝肽子序列

1.金币

问题描述：

国王将金币作为工资，发放给忠诚的骑士。第一天，骑士收到一枚金币；之后两天（第二天和第三天），每天收到两枚金币；之后三天（第四、五、六天），每天收到三枚金币；之后四天（第七、八、九、十天），每天收到四枚金币......；这种工资发放模式会一直这样延续下去：当连续 NN 天每天收到 N枚金币后，骑士会在之后的连续 N+1 天里，每天收到 N+1枚金币。

请计算在前 K 天里，骑士一共获得了多少金币。

输入描述

输入只有 1 行，包含一个正整数 K （1≤K≤104），表示发放金币的天数。

输出描述

输出只有 1 行，包含一个正整数，即骑士收到的金币数。

k=int(input())

l=0
r=10001

while l+1!=r:
    mid=(l+r)//2
    if (mid+1)*mid//2else:
        r=mid
s=r*(r+1)*(2*r+1)//6-(r*(r+1)//2-k)*r
print(s)

#金币

题解分析:

按照题意把前几个数字列出来1,2,2,3,3,3,4,4,4,4....

然后分组[1],[2,2],[3,3,3],[4,4,4,4]...，我们发现第i组一共有i个数

现在，我们把刚刚列出来的'1,2,2,3,3,3,4,4,4,4....'序列的‘1’的下标设为1，下标为几，就代表第几天，很合理。

那么，第1组最后一个数字下标是1，第2组最后一个数字下标是3（1+2）

第3组最后一个数字下标是6（1+2+3）...第n组最后一个数字下标是(1+2..+n)=(1+n)*n/2

说明第n组的最后一天是(1+n)*n/2。

现在题目告诉我们第K天，叫我们求1—K天金币和：S，现在，如果我们能确定K天在第P组，就能求出S。原因是这样：如果知道K在第P组，那么前P组金币和：

1^2+2^2+...p^2=(n)(n+1)(2n+1)//6,n=p代入，那么S<=(p)(p+1)（2p+1）/6

那么还需要进一步确定，K在P组第几个位置，就是说我们在(p)(p+1)（2p+1）/6的基础上减去多算的几天就能得到S。由于K代表的是第K天，我们由知道P组最后一个下标为p*(p+1)/2，也就是p组最后一天对应的是p*(p+1)/2天，那么就有p*(p+1)/2-K这么多天的金币被多算了，由于p组里面每一天得到的金币都说p，那么多算的金币总和=p*（p*(p+1)/2-K）

2.优秀的拆分

题目描述

一般来说，一个正整数可以拆分成若干个正整数的和。

例如，1=1，10=1+2+3+4 等。对于正整数 n 的一种特定拆分，我们称它为“优秀的”，当且仅当在这种拆分下，n 被分解为了若干个不同的 2 的正整数次幂。注意，一个数 x 能被表示成 2 的正整数次幂，当且仅当 x 能通过正整数个 2 相乘在一起得到。

例如，10=8+2=2^3+2^1是一个优秀的拆分。但是，7=4+2+1=2^2+2^1+2^0 就不是一个优秀的拆分，因为 1 不是 2 的正整数次幂。

现在，给定正整数 n，你需要判断这个数的所有拆分中，是否存在优秀的拆分。若存在，请你给出具体的拆分方案。

输入描述

输入只有一行，一个整数 n (1≤n≤107)，代表需要判断的数。

输出描述

如果这个数的所有拆分中，存在优秀的拆分。那么，你需要从大到小输出这个拆分中的每一个数，相邻两个数之间用一个空格隔开。可以证明，在规定了拆分数字的顺序后，该拆分方案是唯一的。

若不存在优秀的拆分，输出 -1。 

n=int(input())

if n%2==1:
    print(-1)
else:
    t=[]
    x=bin(n)[2:][::-1]
    for i in range(len(x)):
        if 2**i*int(x[i])>0:
            t.append(2**i*int(x[i]))
    t=t[::-1]
    for j in range(len(t)-1):
        print(t[j],end=' ')
    print(t[-1])

 题解分析: 

按照题意，给定一个正整数n,   n可以表示为n=2^a+2^b+2^c...

a,b,c...互异且都大于0，求这个方案，并按照降序输出。（由题目‘当且仅当’信息可得，这种拆分方案唯一）那么只需要把n转化为二进制（用PY内部自带函数bin），因为一个数转化为二进制后一定可以表述成上述形式：比如二进制（1001）=2^0*1+2^1*0+2^2*0+2^3*1，利用一个for循环，存入列表，最后遍历列表逐个打印出来就好了。

3.穿越雷区

问题描述：X星的坦克战车很奇怪，它必须交替地穿越正能量辐射区和负能量辐射区才能保持正常运转，否则将报废。
　　某坦克需要从A区到B区去（A，B区本身是安全区，没有正能量或负能量特征），怎样走才能路径最短？

　　已知的地图是一个方阵，上面用字母标出了A，B区，其它区都标了正号或负号分别表示正负能量辐射区。
　　例如：
　　A + - + -
　　- + - - +
　　- + + + -
　　+ - + - +
　　B + - + -

　　坦克车只能水平或垂直方向上移动到相邻的区。

　　数据格式要求：

　　输入第一行是一个整数n，表示方阵的大小， 4<=n<100
　　接下来是n行，每行有n个数据，可能是A，B，+，-中的某一个，中间用空格分开。
　　A，B都只出现一次。

　　要求输出一个整数，表示坦克从A区到B区的最少移动步数。
　　如果没有方案，则输出-1

　　例如：
　　用户输入：
　　5
　　A + - + -
　　- + - - +
　　- + + + -
　　+ - + - +
　　B + - + -

　　则程序应该输出：
　　10

n=int(input())
dp=[]
for i in range(n):
    t=input().split()
    if 'A' in t:
        st=(i,t.index('A'))
    if 'B' in t:
        end=(i,t.index('B'))
    dp.append(t)


pre={}
dx=[-1,1,0,0]
dy=[0,0,1,-1]
queue=[st]
def judge(x,y,dir):
    if 0<=x<=n-1 and 0<=y<=n-1:
        if dir!=dp[x][y]:
            if (x,y) not in pre.keys():
                return True
    return False
        
    
def bfs():
    while queue:
        tmp=queue.pop(0)
        dir=dp[tmp[0]][tmp[1]]
        if tmp==end:
            step=1
            while pre[tmp]!=st:
                tmp=pre[tmp]
                step+=1
            print(step)
            break
        else:
            for i in range(4):
                nx,ny=tmp[0]+dx[i],tmp[1]+dy[i]
                if judge(nx,ny,dir):
                    queue.append((nx,ny))
                    pre[(nx,ny)]=tmp
    else:
        print('-1')
            
    
bfs()
#穿越雷区

 题解分析: 

一道标准BFS模板题，不过多了一个判断：要求两点标记互异，关于BFS小郑在下面这两篇文章讲解的很详细了，需要自取

【蓝桥杯真题】18天Python组冲刺 心得总结_Py小郑的博客-CSDN博客 

蓝桥杯 迷宫 二叉树 真题_Py小郑的博客-CSDN博客

4.蓝肽子序列

题目描述

L 星球上的生物由蛋蓝质组成，每一种蛋蓝质由一类称为蓝肽的物资首尾连接成一条长链后折叠而成。

生物学家小乔正在研究 L 星球上的蛋蓝质。她拿到两个蛋蓝质的蓝肽序列，想通过这两条蓝肽序列的共同特点来分析两种蛋蓝质的相似性。

具体的，一个蓝肽可以使用 1 至 5 个英文字母表示，其中第一个字母大写，后面的字母小写。一个蛋蓝质的蓝肽序列可以用蓝肽的表示顺序拼接而成。

在一条蓝肽序列中，如果选取其中的一些位置，把这些位置的蓝肽取出，并按照它们在原序列中的位置摆放，则称为这条蓝肽的一个子序列。蓝肽的子序列不一定在原序列中是连续的，中间可能间隔着一些未被取出的蓝肽。

如果第一条蓝肽序列可以取出一个子序列与第二条蓝肽序列中取出的某个子序列相等，则称为一个公共蓝肽子序列。

给定两条蓝肽序列，找出他们最长的那个公共蓝肽子序列的长度。

输入描述

输入两行，每行包含一个字符串，表示一个蓝肽序列。字符串中间没有空格等分隔字符。

其中有 ，两个字符串的长度均不超过 1000

输出描述

输出一个整数，表示最长的那个公共蓝肽子序列的长度。

a=input()
b=input()
import re
def f(x):
    t=[]
    for i in range(len(x)):
        if ord(x[i])<97:
            t.append(i)
    r=[]
    for i in range(len(t)-1):
        r.append(x[t[i]:t[i+1]])
    r.append(x[t[-1]:])
    return r
def same(x,y):
    return 1 if x==y else 0
a=f(a)
b=f(b)
#dp[i][j]代表a以下标i为结尾的字符串和b以下标为j结尾的字符串的最长子序列长度
if len(a)

  题解分析: 

是经典问题最长公共子序列问题的略微变形，DP问题。

在研究最长公共子序列问题之前，先研究一下最长公共子串问题，两个类似，这个情况更特殊（简单）。

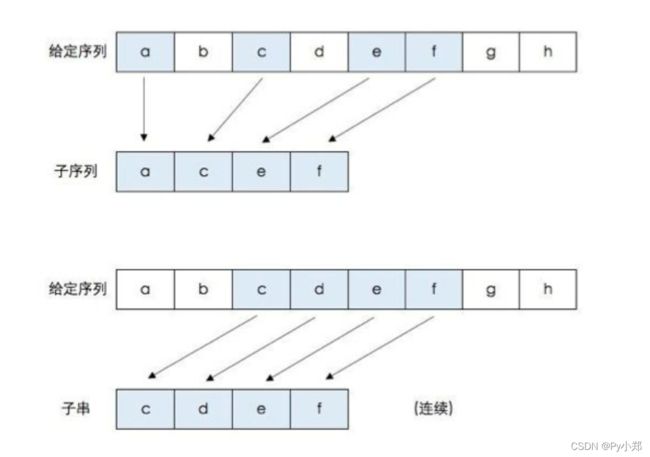
先区分子串和子序列：

显然，不同点：子序列可以是不连续也可以是连续，子串一定是连续 。

相同点：都是从左往右排（维持原先序列的先后顺序）

现在给两个字符串x,y，我们要求x和y的最长公共子串长度

比如x='abcdef',y='bcd'，那么x和y最长公共子串是bcd,长度为3。

可以用dp来解决这类问题，下面定义，

dp[i][j]是是x[0…i] 与y[0…j] 的从最右边开始相同的子串的长度

如果x[i]=y[j]，那么递推关系:dp[i][j]=dp[i-1][j-1]+1

如果x[i]!=y[j],那么递推关系：dp[i][j]=0（最右边不相同了，长度当然为0）

 然后按需赋予初值.

接下来研究最长公共子序列长度：

定义dp[i][j]为以x下标为i的字符结尾的字符串x[0...i]与以y下标为j的字符结尾的字符串y[0..j]的最长公共子序列长度

研究递推关系：和最长公共字串不同，如果x[i]！=y[j],那么dp[i][j]不为0，很显然，因为我们在研究子序列。这是一个区别！！

如果x[i]==y[j],那么显然,dp[i][j]=dp[i-1][j-1]+1

意思是：x下标为i-1的字符结尾的字符串x[0...i-1]与以y下标为j-1的字符结尾的字符串y[0..j-1]的最长公共子序列长度+1

如果x[i]!=y[j]：那字符串x[0...i]和字符串y[0..j]的最长公共子序列长度

为L=max(dp[i-1][j],dp[i][j-1])，可以这样想，因为我们知道x[i]!=y[j]，回到定义：

dp[i][j]为以x下标为i的字符结尾的字符串x[0...i]与以y下标为j的字符结尾的字符串y[0..j]的最长公共子序列长度

所以x和y各自的末字符（强调”“最后一个”“这个概念，而不是末字符的内容（是什么并不重要））就不会对L作出贡献。那到底dp[i][j]等于什么？那么不妨退一步，若取x的前i-1个字符串，取y的前j个子串，那么如果已知dp[i-1][j]，dp[i][j]就可能等于它，因为相当于x的第i个字符x[i]存不存在已经对dp[i][j]没有影响了，这又是因为x[i]!=y[j]。同理，取y的前j-1个字符，取x的前i个字符，dp[i][j]就可能等于它，因为相当于y的第j个字符y[j]存不存在已经对dp[i][j]没有影响了。然后我们比较这两个取最大值，就是最优解。

你可能疑惑的地方：为什么不能是dp[i][j]=max(dp[i-2][j],dp[i][j-2])甚至i-3,j-3。

问题在于，我们要求最长的子序列长度，如果长度尽可能越长，那么子序列长度增加的可能就越大。

写在最后 

蓝桥杯临近 你是否已经做好了充足的准备?

借用小羊的一句话“只要路是对的，就不害怕遥远”。