大力飞砖之DFS与并查集(中-下)
文章目录
- 前言
- 并查集
-
- 集合表示法
- 树状表示法
-
- Parent “数组”
- 组装模板
- DFS搜索并查集
-
- 题目
-
- 手动搜索
- 转换计算机
-
- (补充)基于“交换数组位置的全排列”
前言
mad,距离蓝桥杯越来越近了,三天,我除了第二天整个八经的去玩了一下蓝桥杯算法,剩下两天都在玩Pytorch,诶,摆烂了!
那么今天也是无意在逛社区的时候,发现有一篇文章在说这个玩意,看了看,发现怎么说呢,比我还水,还上热榜了,要将咱们就从最简单的开始讲。
不过他举的例子,也就是题目还可以,咱们待会仔细地讲完并查集和多种代码之后,咱们再来说说这个一题多解。
这个,没记错的话上数据结构的时候是讲过的,虽然我也没怎么听课,不过应该是图里面的内容。
并查集
直接说着玩意儿能够干啥,其实就是分类。
这里给出相关例题
(没错也是从这篇博客找到的)
不过这个博主讲的不是很好,题目到是挺好找的(他的博客适合有点子基础忘了怎么写代码的人,但是我不喜欢这样,要么你别讲,要么你讲好一点,通透一点,不然我直接去B站找视频多香)

例如:输入
5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17
这样一来问题就简单了。
不过在这里我主要不是说这个题目怎么做,而是给出模板,主要是并查集的模板,然后是并查集的搜索。
集合表示法
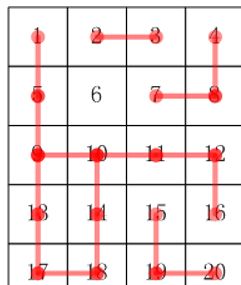
在这里咱们主要是分类嘛,例如刚刚给到的输入例子。
和上面的那张图片,很明显是分为了5个类嘛。那么首先最好想到的自然就是直接使用我们的Set去分类,由于是使用我们的Set,所以最好情况下时间复杂度也是O(1),最坏也是O(log n)(以Java8为例)用另一种最坏也是这样的。
不过在咱们实现的过程当中的话由于涉及到分类,所以最坏应该是O Nlog(n) 这个N是指最后分出来的类。n 也是 每一个类别里面的数量。
所以在java里面你只需要准备这样的一个数据结构

其中这个Node 是我们自己定义的节点
public class Node {
int value;
public Node(int val) {
this.value=val;
}
@Override
public boolean equals(Object obj) {
// TODO Auto-generated method stub
if(obj instanceof Node) {
Node node = (Node) obj;
return node.value==this.value;
}
return false;
}
public String toString() {
return "node [value=" + value + "]";
}
}
所以在加入元素的时候,我们可以这样干。
public static void add(Node node1,Node node2) {
//添加node在我们的map里面
boolean flag=false;
if(index==0) {
index++;
map.put(index, new HashSet<Node>());
//初始化创建一个Set
flag = true;
}
if(flag) {
//添加第一条边
Set<Node> set = map.get(index);
set.add(node1);set.add(node2);
flag=false;//第一条边添加完毕
}
//开始添加后面的边
boolean find = false;
for(Integer key:map.keySet()) {
Set<Node> set = map.get(key);
if(set.contains(node1)||set.contains(node2)) {
set.add(node1);set.add(node2);
find=true;
break;
}
}
if(!find) {
//没找到,说明此时的边不属于那个集合
index++;
HashSet<Node> hashSet = new HashSet<Node>();
hashSet.add(node1);hashSet.add(node2);
map.put(index,hashSet);
}
}
这个就是模板核心代码,如果套在上面的拿个题目的话,你只需要稍微改动一下,先生成所有点,存起来,然后把对应的边存起来也就是使用add方法,然后把剩下的元素分别归为一类就好了。
不过这个是最好想到最好写的,时间复杂度的话就要看情况了,不好说。
树状表示法
这个的话就是要使用到parent数组了。
这个数组,主要是用来存储当前节点的父节点的下标的。
同样的任何算法代码都有几个步骤,初始化,中间状态,结束状态(边界)。
所以同样滴首先是初始化
这里的话,也是要考虑一下数据结构,如果是按照上面我们的这种有一个特殊的Node数据结构的话,那么我们这里应该使用HashMap,由于Node没有重复,所以查找时间复杂度最好O(1) 最坏也是O logN 。那么这里的话看你,看你喜欢那种数据结构。如果使用HashMap的话,那么你DFS搜索的时候是会比较方便的。
这个就和我以前做过的一道题目
《风险度量》 进行搜索是类似的,本质上也是一个并查集的搜索,只不过的话只有最多两个并查集,后面的那个七段码随着那个亮着的灯的那个数量的变化也是会改变并查集个数罢了,本质上都是一样的。
X星系的的防卫体系包含 n 个空间站。这 n 个空间站间有 m 条通信链路,构成通信网。
两个空间站间可能直接通信,也可能通过其它空间站中转。对于两个站点x和y (x != y), 如果能找到一个站点z,使得: 当z被破坏后,x和y无法通信,则称z为关于x,y的关键站点。
显然,对于给定的两个站点,关于它们的关键点的个数越多,通信风险越大。
你的任务是:已知网络结构,求两站点之间的通信风险度,即:它们之间的关键点的个数。
输入数据第一行包含2个整数n(2 <= n <= 1000), m(0 <= m <= 2000),分别代表站点数,链路数。
空间站的编号从1到n。通信链路用其两端的站点编号表示。 接下来m行,每行两个整数 u,v (1 <= u, v <= n; u !=
v)代表一条链路。 最后1行,两个数u,v,代表被询问通信风险度的两个站点。输出:一个整数,如果询问的两点不连通则输出-1.
例如: 用户输入: 7 6
1 3
2 3
3 4
3 5
4 5
5 6
1 6 则程序应该输出: 2
资源约定: 峰值内存消耗(含虚拟机) < 256M CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
java选手注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
java选手注意:主类的名字必须是:Main,否则按无效代码处理。c/c++选手注意: main函数需要返回0 c/c++选手注意: 只使用ANSI C/ANSI C++
标准,不要调用依赖于编译环境或操作系统的特殊函数。 c/c++选手注意: 所有依赖的函数必须明确地在源文件中 #include ,
不能通过工程设置而省略常用头文件。提交程序时,注意选择所期望的语言类型和编译器类型。
这个的题解代码是这样的
class Main5{
//这里分多种情况,首先如果只有一条路,那么都是关键点,如果有多条路,并且存在直接相连的点也是没有关键点的
//除了上面的情况下,被经过的点最多的点为关键点,所以简单了。
static int ways=0;
static int keypoint=0;
static HashMap<Integer,ArrayList<Integer>> map;
static ArrayList<ArrayList<Integer>> routers;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int numbers = scanner.nextInt();
int links = scanner.nextInt();
//保存格式为
/**
* 1-->2
* 2-->3
* 3-->4-->5
* 5-->6
*/
map = new HashMap<Integer, ArrayList<Integer>>();
routers = new ArrayList<ArrayList<Integer>>();
for (int i = 0; i < links; i++) {
int key = scanner.nextInt();
int value = scanner.nextInt();
addmapList(map,key,value);
}
int start = scanner.nextInt();
int target = scanner.nextInt();
ArrayList<Integer> startkeys = map.get(start);
find(startkeys,target,new ArrayList<Integer>());
if (ways==0){
System.out.println(-1);
}else {
if(ways==1){
keypoint = routers.get(0).size();//只有一条路,都是关键点
}else {
if(keypoint==-1){
System.out.println(0);
}else {
//最后一种情况
int[] points = new int[numbers];
for (ArrayList<Integer> router : routers) {
for (Integer integer : router) {
points[integer]++;
}
}
int max = max(points);
keypoint = 0;
for (int i = 0; i < points.length; i++) {
if(points[i]==max){
keypoint++;
}
}
}
}
}
System.out.println(keypoint);
}
public static int max(int [] a){
int max = a[0];
for (int i = 0; i < a.length; i++) {
if(a[i]>max){
max = a[i];
}
}
return max;
}
public static void find(ArrayList<Integer> keyList,int target,ArrayList<Integer> router){
if(keyList.size()==0){
return;
}
for (Integer key:keyList){
if(key==target){
ways++;
if(router.size()==0 && ways>1){
keypoint = -1;//存在直接相连的链路,直接没有关键点
}
routers.add(new ArrayList<>(router));
return;
}
if(map.containsKey(key)){
ArrayList<Integer> findvalue = map.get(key);
router.add(key);
find(findvalue,target,router);
router.remove(router.size()-1);
}else {
return;
}
}
}
public static void addmapList(HashMap<Integer,ArrayList<Integer>> map,Integer key,Integer value){
if(map.containsKey(key)){
ArrayList<Integer> temp = map.get(key);
temp.add(value);
map.put(key,temp);
}else {
ArrayList<Integer> temp1 = new ArrayList<>();
temp1.add(value);
map.put(key,temp1);
}
}
}
Parent “数组”
由于实现的方式有点多,那么这里我还是按照那个传统的使用数组的形式来说明,两者之间无非是换了个数据结构的问题。
先举个例子,这个数组长啥样,知道这个玩意长啥样之后,俺们就好办了。

接下来,如果我们要表示关系1–2–3 和 4–5 的话还不简单
假设,此时它输入的数据格式是这样的
1–2
2–3
4–5
那么此时,我们可以这样干,直接先把1当做父节点
然后数组先这样变
0 1 1 3 4 5 6
0 1 2 3 4 5 6 下标表示元素
然后2–3
这样表示
先找到2的父节点 parent[2]看看是不是和parent[3]相等,不相等,我们把2–3的关系建立起来
也就是 parent[3]=findParent(parent[2])
这里定义一个方法,findParent是专门用来找父节点下标的。
0 1 1 1 4 5 6
0 1 2 3 4 5 6 下标表示元素
那么这个方法的代码可以这样写
public static int findParent(int a) {
//当自己等于自己的时候显然我们就是找到了父节点,也就是根根节点
if(a==Parentr[a]){
return a;
}
return findParent(Parent[a]);
作用就是找到1–2–3
里面找到2的父节点,再找到父节点的父节点,知道找到位置,然后返回,就是深度搜索过程嘛。
同样的合并也是一样的
private static void union(int a, int b) {//合并
a_=findParen(Parent[a]);
b_=findParen(Parent[b]);
if(a_!=b_){
Parent[b]=a_;
}
}
这里是1–2 过来吧 2的父节点设置为1,你也可以反过来,随便。
不过在那里家伙写的代码里面的话,是和我这反过来的,这个无伤大雅。
组装模板
完整代码和简单,这里还是把流程模板给一遍。
初始化
中间过程
for (int i = 0; i < k; i++) {
int a=scanner.nextInt();
int b=scanner.nextInt();
if(findParent(a)!=findParent(b)){
union(a,b);
}
}
怎么说,好就好在了数据结构,如果是复杂数据结构,我建议还是使用HashMap.原理也一样,只是要去key-value里面找。
DFS搜索并查集
这里就以那个 七段码 这个题目为案例:
题目
怎么说呢,一说到这个,我又想到了另一个题目。
《滑动解锁》
滑动解锁是智能手机一项常用的功能。你需要在3x3的点阵上,从任意一个点开始,反复移动到一个尚未经过的"相邻"的点。这些划过的点所组成的有向折线,如果与预设的折线在图案、方向上都一致,那么手机将解锁。
所谓两个点“相邻”:当且仅当以这两个点为端点的线段上不存在尚未经过的点。
此外,许多手机都约定:这条折线还需要至少经过4个点。
为了描述方便,我们给这9个点从上到下、从左到右依次编号1-9。即如下排列:
1 2 3
4 5 6
7 8 9
那么1->2->3是非法的,因为长度不足。
1->3->2->4也是非法的,因为1->3穿过了尚未经过的点2。
2->4->1->3->6是合法的,因为1->3时点2已经被划过了。
某大神已经算出:一共有389112种不同的解锁方案。没有任何线索时,要想暴力解锁确实很难。
不过小Hi很好奇,他希望知道,当已经瞥视到一部分折线的情况下,有多少种不同的方案。
遗憾的是,小Hi看到的部分折线既不一定是连续的,也不知道方向。
例如看到1-2-3和4-5-6,
那么1->2->3->4->5->6,1->2->3->6->5->4, 3->2->1->6->5->4->8->9等都是可能的方案。
你的任务是编写程序,根据已经瞥到的零碎线段,求可能解锁方案的数目。
输入:
每个测试数据第一行是一个整数N(0 <= N <= 8),代表小Hi看到的折线段数目。
以下N行每行包含两个整数 X 和 Y (1 <= X, Y <= 9),代表小Hi看到点X和点Y是直接相连的。
输出:
对于每组数据输出合法的解锁方案数目。
例如:
输入:
8
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
程序应该输出:
2
再例如:
输入:
4
2 4
2 5
8 5
8 6
程序应该输出:
258
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
java选手注意:不要使用package语句。不要使用jdk1.7及以上版本的特性。
java选手注意:主类的名字必须是:Main,否则按无效代码处理。
c/c++选手注意: main函数需要返回0
c/c++选手注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
c/c++选手注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交程序时,注意选择所期望的语言类型和编译器类型。
两道题目怎么说呢,在有些地方上很类似。也比较巧妙。
当然感兴趣的到这里去看:https://blog.csdn.net/FUTEROX/article/details/123170908
我们这边还是说说,关于这道题目吧。
说句大实话,不看人家代码,我可能真滴写不出来。不过还好是一个填空题,所以我们可以考虑纯手写。
手动搜索
我们先来模拟一下手动搜索,不然的话看人家代码说实话有点懵。
首先手动模拟,我们应该是这样的
假设亮1个灯:按照条件查看有没有相连,然后在符合条件的情况下去搜索全部情况。
假设亮2个灯:如上
假设亮3个灯:
应该很快可以手动枚举出情况。
转换计算机
手动转换简单,那么如果是丢给计算机,那么我们需要解决那些问题。
第一个显然是如何判断,两个玩意有没有相连,如何表示abcdefg这样的灯管。
第二个就是如何模拟假设亮几个灯的情况,在DFS里面。
第三个就是怎么和并查集扯上关系。
所以只要解决了这个三个大问题,那么接下来就好办了。
首先对于第一个问题,很显然,我们是可以直接创建一个图来表示两个段有没有相连的,那么最简单的方式就是使用矩阵,那么此时我们就可以直接使用1234567表示abcdefg了
也就是这样
![]()
第二个问题
如何假设我们亮灯的情况,这块的话我们联想到我们先前给出的全排列模板呀,这个used数组,不就刚好可以模拟亮几个灯的情况嘛。
第三个问题
为什么是并查集
这个怎么说呢,我们以1号为节点找和1相连的不就是相当于找那个1位父节点的嘛
然后以2为开头,以此类推
代码
//考虑到这个是一道填空题,所以在一定程度上可以手动枚举
public class DFS并查集 {
static int ismap[][]=new int[8][8];//存储灯管的连通情况
static int Parent[]=new int[8];//并查集的父节点
static boolean used[]=new boolean[8];
static int ans=0;
public static void main(String[] args) {
//连边建图,这题的关键点之一就是创建这个图,用于判断能不能行
//a b c d ismap f g
//1 2 3 4 5 6 7
//ismap[i][j]=1表示i灯光和j灯光是相互连接的
ismap[1][2]=ismap[1][6]=1;
ismap[2][1]=ismap[2][7]=ismap[2][3]=1;
ismap[3][2]=ismap[3][4]=ismap[3][7]=1;
ismap[4][3]=ismap[4][5]=1;
ismap[5][4]=ismap[5][6]=ismap[5][7]=1;
ismap[6][1]=ismap[6][5]=ismap[6][7]=1;
dfs(1);
System.out.println(ans);
}
static void dfs(int n){
if(n==8){
// 当 n==8的时候,意味者7个节点都被访问了
for (int i = 1; i <=7 ; i++) {//初始化每一个父节点
Parent[i]=i;
}
for (int i = 1; i <=7 ; i++) {
for (int j = 1; j <=7 ; j++) {
if(used[i]&&used[j]&&ismap[i][j]==1){//如果当前两盏相互连接的灯处于打开的状态则放在一个集合里
Parent[findParent(i)]=findParent(j);//合并操作
}
}
}
int cnt=0;//用来记录联通情况
for (int i = 1; i <=7 ; i++) {
if(used[i]&&Parent[i]==i){
cnt++;
}
}
//当有且仅有一种联通亮灯情况的时候才合法,这个时候ans++
if(cnt==1)ans++;
return;
}
used[n]=true;//当前第n盏灯是打开的
dfs(n+1);
used[n]=false;//当前第n盏灯是关闭的
dfs(n+1);
}
static int findParent(int x){
if(x==Parent[x]){
return x;
}else {
Parent[x]=findParent(Parent[x]);
return Parent[x];
}
}
}
当然这里插入一个题外话,就是关于全排列的第二种写法,说实话我没注意以,这个写法要原来我写的好一点,优化了used数组。
(补充)基于“交换数组位置的全排列”
public class Main{
public static void main(String[] args) {
int[] arr = { 1, 2, 3 };
fullSort(arr, 0, arr.length - 1);
}
public static void fullSort(int[] arr, int start, int end) {
for(int i=start;i<end;i++){
//换位置
swap(arr,i,start)
fullSort(arr,start+1,end)
swap(arr,i,start)//换回来
}
private static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
这里简单说一下原理。
有两个需要注意到的点
123 的全排列是相当于
1 和 23 的全排列
然后 23 的全排列相当于
2 和 3的全排列
也就是踢皮球的思想嘛。
所以 fullSort(arr,start+1,end)就是把2,3全排列一下,以此类推然后和1组合
swap 的作用是,1 开头的全排列,然后是2开头的,有一个交换的意思。
我们这边简单模拟一下运行过程(这个实际的运算过程其实和我们设计递归的过程不太一样)
1----》 第一层进入swap 函数 1 2 3
2----》 第二层进入递归 swap 函数 1 2 3
3----》 第三层进入递归 swap 函数 1 2 3 输出 123 跳出返回第二层
2----》返回第二层 进入第二个swap 123
2----》循环未结束 再次 进入第一个swap 1 3 2
之后有一个细节是:
swap(arr,i,start)//换回来
有些的也是
swap(arr,start,i)//换回来
怎么说呢,我前面这样写的目的是输出了之后要进行回溯,所以反过来交换回去
后者,我看了看人家的思想是说交换完毕后,由于下一次交换是由上一次的状态取决的,所以必须回溯到上一个状态