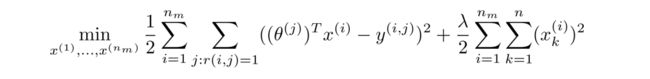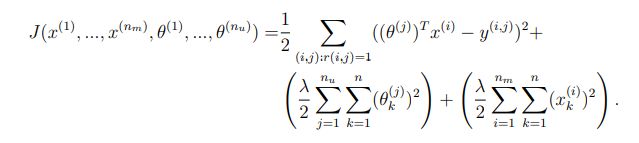【机器学习】推荐算法(附例题代码)

往期文章
【机器学习】回归分析
【机器学习】Logistic回归
【机器学习】神经网络
【机器学习】支持向量机
【机器学习】主成分分析与聚类分析

推荐算法

问题引入

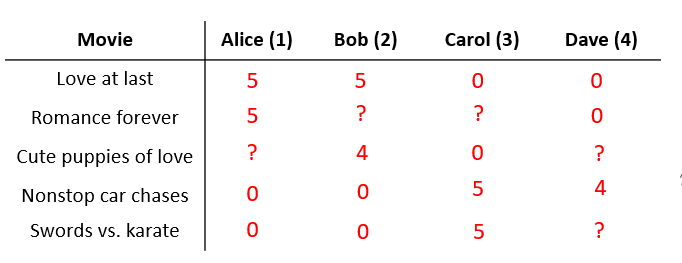
现在有一个预测电影评分的问题，共有5部电影，由4个用户进行评分，评分等级为0~5颗星，其中打？号的表示未看过此电影，不作评价。

先介绍一些符号代表的含义：

$n_u$：用户数量。

$n_m$：电影数量。

$r(i,j)$：如果等于1，这说明用户$j$已经给电影$i$评分，等于0则没有。

$y^{(i,j)}$：用户$j$给电影$i$的评分，只有当$r(i,j)$=1时该项才有意义。

推荐系统要做的是根据给出$r(i,j)$和$y^{(i,j)}$的数据，然后去查找那些没有被评分的电影，并试图预测这些电影的评价星级。

基于内容的推荐算法

还是上面的例子：

我们知道了$n_u$=4，$n_m$=5，那么怎样才能预测那些未知的值呢？

现在我们有一个关于电影的特征集，分别是$x_1$和$x_2$，$x_1$表示该电影为爱情片的程度，$x_2$则表示该电影为动作片的程度。

那么每部电影我们都可以得到一个向量$x^{(i)}$。

例如第一步电影的特征可表示为（其中1是偏置项）：

$$x^{(1)}=\left[\begin{array}{c}1\\ 0.9\\ 0\end{array}\right]\in R^{n+1}$$

那么我们可以把这个问题看成是一个线性回归问题，对于每个用户$j$，我们都要学习得到一个参数向量${\theta }^{(j)}$，然后预测用户$j$评价电影$i$的值，也就是$({\theta }^{(j)}{)}^T{x}^{(i)}$.

参数的学习也和线性回归问题类似。

单个用户参数学习：

多个用户的参数学习：

梯度下降：

协同过滤

如果每部电影的特征没有给出，也就是说一部电影属于爱情片还是动作片的程度未知。

但是已知每个用户的学习参数：

那么我们同样可以推出电影对应的特征。

例如第一部电影，我们只需满足：

$$({\theta }^{(1)}{)}^T{x}^{(1)}\approx 5$$

$$({\theta }^{(2)}{)}^T{x}^{(2)}\approx 5$$

$$({\theta }^{(3)}{)}^T{x}^{(3)}\approx 0$$

$$({\theta }^{(4)}{)}^T{x}^{(4)}\approx 0$$

通过这种方法我们可以得到电影的其他适合的特征。

也就是给定${\theta }^{(1)},...,{\theta }^{(n_u)}$来学习特征$x^{(i)}$:

只学习一部电影的特征：

学习多部电影的特征：

**总结：**系统一开始会随机取一些$\theta$值，有了这些后，我们就可以学习出不同电影的特征$x$，然后又可以前面的推荐算法来学习出一些更好的参数$\theta$，不断迭代，最终结果会收敛于一组合理的电影特征和用户参数。

协同过滤算法

上面我们讨论的协同过滤步骤如下：

1. 给定特征$x^{(1)},x^{(2)},...,x^{(m)}$，估计参数${\theta }^{(1)},...,{\theta }^{(n_u)}$：

2. 利用第一步得到的${\theta }^{(1)},...,{\theta }^{(n_u)}$，估计特征$x^{(1)},x^{(2)},...,x^{(m)}$。

我们要做的是不断重复这些计算，不断优化$\theta$和$x$.

实际上还有一个更有效率的算法，能够将$x$和$\theta$同时计算出来，因此我们定义这个新的代价函数$J$是关于特征$x$和参数$\theta$的函数，其实就是上面两个代价函数的组合：

算法步骤：

1. 初始化$x^{(1)},x^{(2)},...,x^{(m)}，{\theta }^{(1)},...,{\theta }^{(n_u)}$为较小的随机数。
2. 使用梯度下降最小化代价函数$J(x^{(1)},x^{(2)},...,x^{(m)}，{\theta }^{(1)},...,{\theta }^{(n_u)})$。

均值规范化

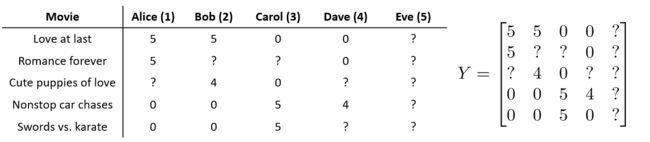
在实际应用中，我们可能会遇到某个用户从未对电影进行过评分的情况，例如下图的Eve：

而我们相应得到的为0，无法对Eve的偏好进行预测。

$${\theta }^{(5)}=\left[\begin{array}{c}0\\ 0\end{array}\right]$$

这时我们可以对每部电影的数据进行均值规范化，求出每部电影评分的均值，然后相应地减去这个均值，等到下面数据：

那么当我们对用户$j$预测其对第$i$部电影的评分时，还需要重新加上均值$u_i$才能得到预测的分数：

$$({\theta }^{(i)}{)}^T(x^{(i)})+u_i$$

因此，对于用户Eve，即使$({\theta }^{(i)}{)}^T(x^{(i)})$这一项为0，但加上均值后就不为0了，此时Eve就有一个初始的电影评分，也就是说，当一个新用户注册后，可以先根据大众喜好进行推荐，然后根据后续用户的选择，评分等再慢慢优化参数。

python实现

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat

data = loadmat('E:\happy\ML&DL\My_exercise\ex8-recommender System\data\ex8_movies')
data

Y,R = data.get('Y'),data.get('R')
Y.shape,R.shape

param_mat = loadmat('E:\happy\ML&DL\My_exercise\ex8-recommender System\data\ex8_movieParams')
param_mat

X, theta = param_mat.get('X'),param_mat.get('Theta')
X.shape,theta.shape

#特征个数10
n_features = 10

def serialize(X, theta):
    return np.concatenate((X.ravel(), theta.ravel()))

def deserialize(params, n_movie, n_user, n_features):
    return params[:n_movie * n_features].reshape(n_movie, n_features), \
           params[n_movie * n_features:].reshape(n_user, n_features)
    
#代价函数
def cost(params, Y, R, n_features):
    n_movie, n_user = Y.shape
    X, theta = deserialize(params, n_movie, n_user, n_features)
    #注意这里只需要计算R=1的
    inner = np.multiply(X @ theta.T - Y, R)
    return np.power(inner, 2).sum() / 2

#梯度
def gradient(params, Y, R, n_features):
    n_movie, n_user = Y.shape
    X, theta = deserialize(params, n_movie, n_user, n_features)
    inner = np.multiply(X @ theta.T - Y, R)  # (1682, 943)
    X_grad = inner @ theta  #（1682， 10）
    theta_grad = inner.T @ X  #（943， 10）
    
    return serialize(X_grad, theta_grad)

#代价函数正规项
def regularized_cost(params, Y, R, n_features, lam=1):
    reg = np.power(params, 2).sum() * (lam / 2)
    return cost(params, Y, R, n_features) + reg

#梯度函数正规项
def regularized_gradient(params, Y, R, n_features, lam=1):
    grad = gradient(params, Y, R, n_features)
    reg = lam * params
    
    return grad + reg

#测试一下代价函数是否正确
cost(serialize(X, theta), Y, R, n_features)

regularized_cost(serialize(X, theta), Y, R, 10)

#将题目数据中给的电影列出来
movie_idx = {}
f = open('E:\happy\ML&DL\My_exercise\ex8-recommender System\data\movie_ids.txt',encoding= 'gbk')
for line in f:
    tokens = line.split(' ')
    tokens[-1] = tokens[-1][:-1]
    movie_idx[int(tokens[0]) - 1] = ' '.join(tokens[1:])

#接下来可以给自己看过的电影打上分数（1-5分）
ratings = np.zeros((1682, 1))
ratings[0] = 4
ratings[6] = 3
ratings[11] = 5
ratings[53] = 4
ratings[63] = 5
ratings[65] = 3
ratings[68] = 5
ratings[97] = 2
ratings[182] = 4
ratings[225] = 5
ratings[354] = 5

Y,R = data.get('Y'),data.get('R')
#将我们的评分添加到943位用户的评分集中
Y = np.append(Y, ratings, axis=1)  
R = np.append(R, ratings != 0, axis=1)
Y.shape, R.shape

初始化$x^{(1)},x^{(2)},...,x^{(m)}，{\theta }^{(1)},...,{\theta }^{(n_u)}$为较小的随机数，同时进行标准化。

n_features = 50
n_movie, n_user = Y.shape
lr = 10 #学习率
X = np.random.standard_normal((n_movie, n_features))
theta = np.random.standard_normal((n_user, n_features))

#归一化
Y_norm = Y - Y.mean()
Y_norm.mean()

模型训练

import scipy.optimize as opt

params = np.concatenate((np.ravel(X), np.ravel(theta)))

res = opt.minimize(fun=regularized_cost,
                   x0=params,
                   args=(Y_norm, R, n_features, lr),
                   method='TNC',
                   jac=regularized_gradient)

res

#训练后的参数
X_trained, theta_trained = deserialize(res.x, n_movie, n_user, n_features)
X_trained.shape, theta_trained.shape

#进行预测
pred = X_trained @ theta_trained.T
final_preds = pred[:, -1] + Y.mean()

final_preds

代码和例题获取

点击文末名片，到公号回复“机器学习”领取，以往的例题代码也一起打包了。

参考资料：

[1] https://www.bilibili.com/video/BV164411b7dx

[2] https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes