卷积网络的平移不变性

1 什么是不变性

【不变性】就是目标发生了变换，但是你依然可以识别出来。在图像任务中，我们希望图像中的目标即使被平移、被旋转或者被缩放，模型都可以识别出来图像的目标。

所以不变性有下面几种：

平移不变性：Translation Invariance
旋转不变性：Rotation Invariance
尺度不变性：scale Invariance
光照不变性：Illumination Invariance
在图像分类任务中，平移不变性就是图像中的目标不管被移动到哪个位置，模型给出的标签应该都是相同的。

【平移不变性对应的有一个概念是平移同变性（translation equivariance），这个是用在图像的目标检测中的，如果输入图像中的目标进行了平移，那么最终检测出来的候选框应该也相应的移动，这就是同时改变。】

2 为什么有平移不变性

主要是由两个原因，一个是卷积，一个是最大池化。

【为什么卷积可以提供平移不变性】 比方说目标是在图像的左上角，经过卷积之后，目标的特征也会在特征图的左上角；目标在图像的左下角，经过相同的卷积核卷积之后，目标的特征也会在特征图的左下角。然后卷积层后面接上一个全连接层进行分类，就算目标位置改变了，但是经过相同的卷积核卷积，然后展开变成全连接层。所以对于全连接层来说，改变的之后特征的位置。可能之前目标的特征是作为全连接的第一个神经元的输入，平移目标位置之后，该特征就作为全连接的最后一个神经元的输入。

不过这种说法想体现的就是，就算目标位置变了，经过相同卷积核提取的特征该有的都有，只是位置变了。

简单地说，卷积+最大池化约等于平移不变性。

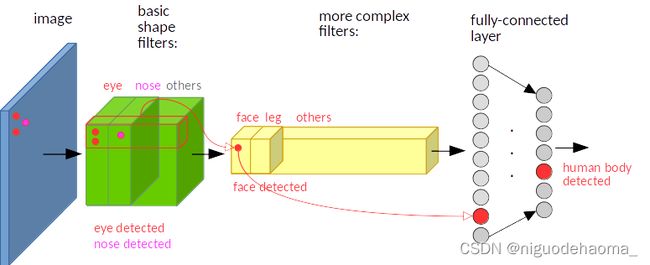
卷积：简单地说，图像经过平移，相应的特征图上的表达也是平移的。下图只是一个为了说明这个问题的例子。输入图像的左下角有一个人脸，经过卷积，人脸的特征（眼睛，鼻子）也位于特征图的左下角。假如人脸特征在图像的左上角，那么卷积后对应的特征也在特征图的左上角。 （如下两幅图所示）

在神经网络中，卷积被定义为不同位置的特征检测器，也就意味着，无论目标出现在图像中的哪个位置，它都会检测到同样的这些特征，输出同样的响应。比如人脸被移动到了图像左下角，卷积核直到移动到左下角的位置才会检测到它的特征。

池化：比如最大池化，它返回感受野中的最大值，如果最大值被移动了，但是仍然在这个感受野中，那么池化层也仍然会输出相同的最大值。这就有点平移不变的意思了。

所以这两种操作共同提供了一些平移不变性，即使图像被平移，卷积保证仍然能检测到它的特征，池化则尽可能地保持一致的表达。

【为什么池化可以提供平移不变性】 我觉得这个相比上面的解释，是有一定的道理的。最大池化层返回感受野中的最大值，如果最大值被移动了，但是仍然在这个感受野中，那么池化层也仍然会输出相同的最大值。这就有点平移不变的意思了。

在参考链接[2]中，给出了几个“池化层具有不变性”的例子：

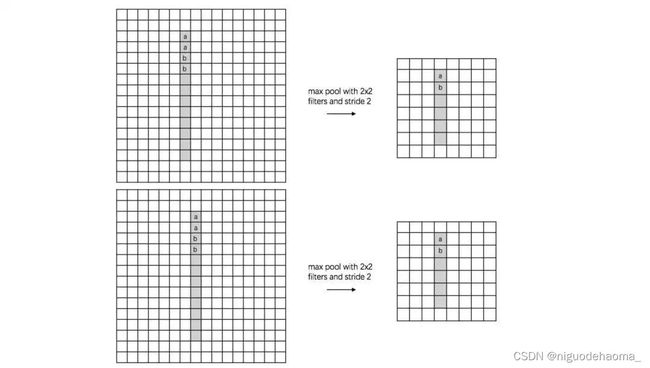
可以看到，同样的数字1，原图中平移了1个像素，但是经过2*2的最大池化层之后，得到了相同的特征图。此外，最大池化层还可以根据类似的原理，得到尺度不变性和旋转不变性：


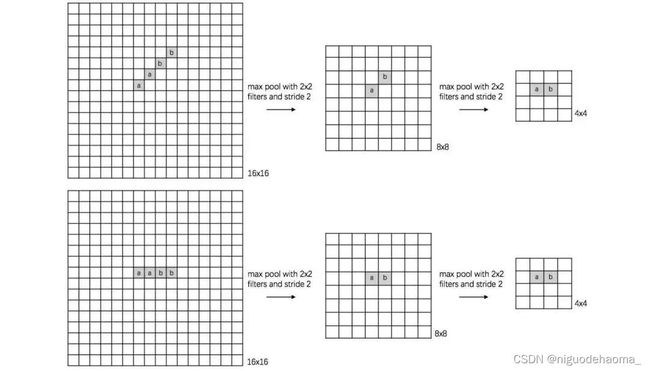
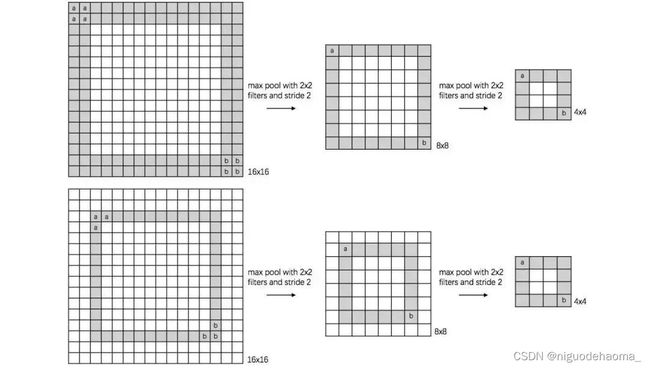
【池化层引入了平移不变性我觉得是比较靠谱的，这也是池化层的重要作用之一：为CNN引入不变性。但是怎么说呢？虽然目前听起来很有道理，在面试的时候被问起来池化层作用的时候我觉得回答上不变性也是不错的，但是下文就会讲解，池化层实际上并没有引入不变性。好像是2019年的一个论文强调了池化层并没有不变性】

3 为什么没有平移不变性

现在卷积网路的图像输入，改变一个像素就可能会得出不同的结构，所以很容易遭到对抗攻击。下面有一个形象的例子：

可以看出来，当平移小鸟的位置的时候，预测结果是有很大的波动的。

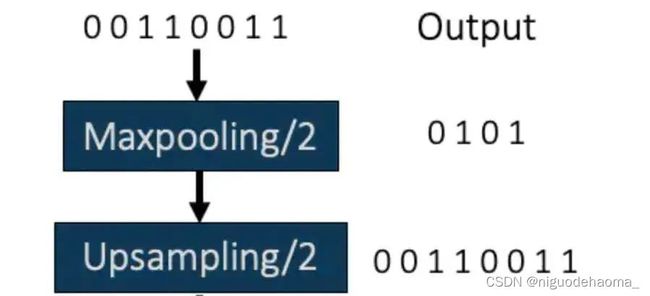
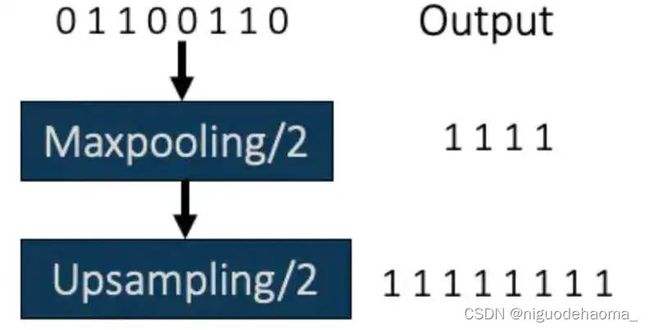
池化层并没有平移不变性。下面是参考链接[3]给出的一个简单的例子，这是一个一维卷积的例子，二维图像类似：

上图是一个没有平移的原始一位数据做了一个1*2的最大池化；

如果对一位数据做了一个平移，那么得到的池化结果就完全不同！这也就是为什么下采样（平均池化层，最大池化层等）没有平移不变性。

4 平移不变性的定义

说了这么多平移不变性，那么平移不变性的具体的严格的定义到底是什么呢？

定义几个数学符号。原始的输入数据为

									X

,经过下采样层变成

									D(X)

,然后再经过上采样得到

									U(D(X))

.(D是Down下采样，U是Up上采样)

【平移不变性】 如果平移之后的输入图像的下采样的上采样与原始输入图像的下采样的上采样相同，那么就是平移不变性。（中文说的太绕嘴了，数学公式清晰）

									U(D(X))=U(D(Xshift))
									Xshift

就是平移之后的输入；

举个例子：

这个就是

									U(D(X))

这个就是

									U(D(Xshift))

可以发现两者并不相等，所以并没有平移不变性。

5 如何实现平移不变性

现在使用的全局平均池化层，就是可以实现平移不变性。依然是用上面的例子：

可以发现，其实不管平移多少，反正得到的数值都是一样的，全局平均池化消除了位置的影响，所以实现了平移不变性。

参考链接：
[1]https://zhangting2020.github.io/2018/05/30/Transform-Invariance/

[2]https://www.zhihu.com/question/36686900

[3]https://www.jianshu.com/p/6041f3e8a583

转载于：
[1] https://cloud.tencent.com/developer/article/1661000

[2] https://codeantenna.com/a/dCn757fOJD