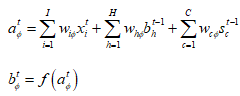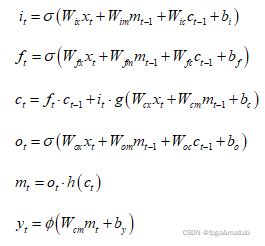【LSTM】基于LSTM网络的人脸识别算法的MATLAB仿真
1.软件版本
matlab2021a
2.本算法理论知识
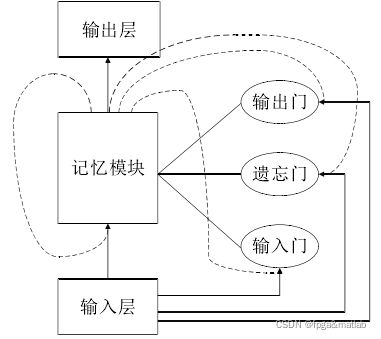
长短时记忆模型LSTM是由Hochreiter等人在1997年首次提出的,其主要原理是通过一种特殊的神经元结构用来长时间存储信息。LSTM网络模型的基本结构如下图所示:
图1 LSTM网络的基本结构
从图1的结构图可知,LSMT网络结构包括输入层,记忆模块以及输出层三个部分,其中记忆模块由输入门(Input Gate)、遗忘门(Forget Gate)以及输出门(Output Gate)。LSTM模型通过这三个控制门来控制神经网络中所有的神经元的读写操作。
LSTM模型的基本原理是通过多个控制门来抑制RNN神经网络梯度消失的缺陷。通过LSTM模型可以在较长的时间内保存梯度信息,延长信号的处理时间,因此LSTM模型适合处理各种频率大小的信号以及高低频混合信号。LSTM模型中的记忆单元中输入门(Input Gate)、遗忘门(Forget Gate)以及输出门(Output Gate)通过控制单元组成非线性求和单元。其中输入门、遗忘门以及输出门三个控制门的激活函数为Sigmoid函数,通过该函数实现控制门“开”和“关”状态的改变。
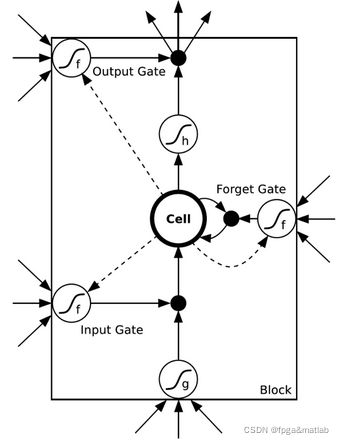
下图为LSTM模型中记忆模块的内部结构图:
图2 LSTM网络的记忆单元内部结构
从图2的结构图可知,LSTM的记忆单元的工作原理为,当输入门进入”开“状态,那么外部信息由记忆单元读取信息,当输入门进入“关”状态,那么外部信息无法进入记忆单元。同理,遗忘门和输出门也有着相似的控制功能。LSTM模型通过这三个控制门将各种梯度信息长久的保存在记忆单元中。当记忆单元进行信息的长时间保存的时候,其遗忘门处于“开”状态,输入门处于“关”状态。
当输入门进入“开”状态之后,记忆单元开始接受到外部信息并进行存储。当输入门进入“关”状态之后,记忆单元暂停接受外部信息,同时,输出门进入“开”状态,记忆单元中保存的信息传输到后一层。而遗忘门的功能则是在必要的时候对神经元的状态进行重置。
对于LSTM网络模型的前向传播过程,其涉及到的各个数学原理如下:
2.遗忘门计算过程如下所示:
3.记忆单元计算过程如下所示:
4.输出门计算过程如下所示:
5.记忆单元输出计算过程如下所示:
对于LSTM网络模型的反向传播过程,其涉及到的各个数学原理如下:
6.输入门计算过程如下所示:
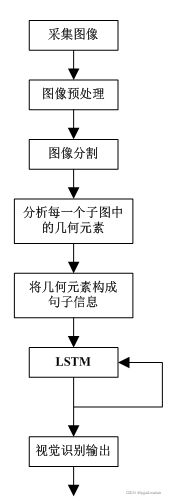
基于LSTM网络的视觉识别算法,其整体算法流程图如下图所示:
图3基于LSTM网络的视觉识别算法流程图
根据图3的算法流程图,本文所要研究的基于LSTM网络的视觉识别算法步骤为:
步骤一:图像的采集,本文以人脸图像为研究对象。
步骤二:图像预处理,根据本章2节的内容对所需要识别的视觉图像进行预处理,获得较为清晰的图像。
步骤三:图像分割,将图像进行分割,分割大小根据采集图像的识别目标和整体场景大小关系进行确定,将原始的图像分割为![]() 大小的子图像。
大小的子图像。
步骤四:子图几何元素提取,通过边缘提取方法,获得每个子图中所包含的几何元素,并将各个几何元素构成句子信息。
步骤五:将句子信息输入到LSTM网络,这个步骤也是核心环节,下面对LSTM网络的识别过程进行介绍。首先,将句子信息通过LSTM的输入层输入到LSTM网络中,基本结构图如下图所示:
图3基于LSTM网络的识别结构图
这里假设LSTM某一时刻的输入特征信息和输出结果为![]() 和,其记忆模块中的输入和输出为和,和表示LSTM神经元的激活函数的输出和隐含层的输出,整个LSTM的训练流程为:
和,其记忆模块中的输入和输出为和,和表示LSTM神经元的激活函数的输出和隐含层的输出,整个LSTM的训练流程为:
3.核心代码
function nn = func_LSTM(train_x,train_y,test_x,test_y);
binary_dim = 8;
largest_number = 2^binary_dim - 1;
binary = cell(largest_number, 1);
for i = 1:largest_number + 1
binary{i} = dec2bin(i-1, binary_dim);
int2binary{i} = binary{i};
end
%input variables
alpha = 0.000001;
input_dim = 2;
hidden_dim = 32;
output_dim = 1;
%initialize neural network weights
%in_gate = sigmoid(X(t) * U_i + H(t-1) * W_i)
U_i = 2 * rand(input_dim, hidden_dim) - 1;
W_i = 2 * rand(hidden_dim, hidden_dim) - 1;
U_i_update = zeros(size(U_i));
W_i_update = zeros(size(W_i));
%forget_gate = sigmoid(X(t) * U_f + H(t-1) * W_f)
U_f = 2 * rand(input_dim, hidden_dim) - 1;
W_f = 2 * rand(hidden_dim, hidden_dim) - 1;
U_f_update = zeros(size(U_f));
W_f_update = zeros(size(W_f));
%out_gate = sigmoid(X(t) * U_o + H(t-1) * W_o)
U_o = 2 * rand(input_dim, hidden_dim) - 1;
W_o = 2 * rand(hidden_dim, hidden_dim) - 1;
U_o_update = zeros(size(U_o));
W_o_update = zeros(size(W_o));
%g_gate = tanh(X(t) * U_g + H(t-1) * W_g)
U_g = 2 * rand(input_dim, hidden_dim) - 1;
W_g = 2 * rand(hidden_dim, hidden_dim) - 1;
U_g_update = zeros(size(U_g));
W_g_update = zeros(size(W_g));
out_para = 2 * zeros(hidden_dim, output_dim) ;
out_para_update = zeros(size(out_para));
% C(t) = C(t-1) .* forget_gate + g_gate .* in_gate
% S(t) = tanh(C(t)) .* out_gate
% Out = sigmoid(S(t) * out_para)
%train
iter = 9999; % training iterations
for j = 1:iter
% generate a simple addition problem (a + b = c)
a_int = randi(round(largest_number/2)); % int version
a = int2binary{a_int+1}; % binary encoding
b_int = randi(floor(largest_number/2)); % int version
b = int2binary{b_int+1}; % binary encoding
% true answer
c_int = a_int + b_int; % int version
c = int2binary{c_int+1}; % binary encoding
% where we'll store our best guess (binary encoded)
d = zeros(size(c));
% total error
overallError = 0;
% difference in output layer, i.e., (target - out)
output_deltas = [];
% values of hidden layer, i.e., S(t)
hidden_layer_values = [];
cell_gate_values = [];
% initialize S(0) as a zero-vector
hidden_layer_values = [hidden_layer_values; zeros(1, hidden_dim)];
cell_gate_values = [cell_gate_values; zeros(1, hidden_dim)];
% initialize memory gate
% hidden layer
H = [];
H = [H; zeros(1, hidden_dim)];
% cell gate
C = [];
C = [C; zeros(1, hidden_dim)];
% in gate
I = [];
% forget gate
F = [];
% out gate
O = [];
% g gate
G = [];
% start to process a sequence, i.e., a forward pass
% Note: the output of a LSTM cell is the hidden_layer, and you need to
for position = 0:binary_dim-1
% X ------> input, size: 1 x input_dim
X = [a(binary_dim - position)-'0' b(binary_dim - position)-'0'];
% y ------> label, size: 1 x output_dim
y = [c(binary_dim - position)-'0']';
% use equations (1)-(7) in a forward pass. here we do not use bias
in_gate = sigmoid(X * U_i + H(end, :) * W_i); % equation (1)
forget_gate = sigmoid(X * U_f + H(end, :) * W_f); % equation (2)
out_gate = sigmoid(X * U_o + H(end, :) * W_o); % equation (3)
g_gate = tanh(X * U_g + H(end, :) * W_g); % equation (4)
C_t = C(end, :) .* forget_gate + g_gate .* in_gate; % equation (5)
H_t = tanh(C_t) .* out_gate; % equation (6)
% store these memory gates
I = [I; in_gate];
F = [F; forget_gate];
O = [O; out_gate];
G = [G; g_gate];
C = [C; C_t];
H = [H; H_t];
% compute predict output
pred_out = sigmoid(H_t * out_para);
% compute error in output layer
output_error = y - pred_out;
% compute difference in output layer using derivative
% output_diff = output_error * sigmoid_output_to_derivative(pred_out);
output_deltas = [output_deltas; output_error];
% compute total error
overallError = overallError + abs(output_error(1));
% decode estimate so we can print it out
d(binary_dim - position) = round(pred_out);
end
% from the last LSTM cell, you need a initial hidden layer difference
future_H_diff = zeros(1, hidden_dim);
% stare back-propagation, i.e., a backward pass
% the goal is to compute differences and use them to update weights
% start from the last LSTM cell
for position = 0:binary_dim-1
X = [a(position+1)-'0' b(position+1)-'0'];
% hidden layer
H_t = H(end-position, :); % H(t)
% previous hidden layer
H_t_1 = H(end-position-1, :); % H(t-1)
C_t = C(end-position, :); % C(t)
C_t_1 = C(end-position-1, :); % C(t-1)
O_t = O(end-position, :);
F_t = F(end-position, :);
G_t = G(end-position, :);
I_t = I(end-position, :);
% output layer difference
output_diff = output_deltas(end-position, :);
% H_t_diff = (future_H_diff * (W_i' + W_o' + W_f' + W_g') + output_diff * out_para') ...
% .* sigmoid_output_to_derivative(H_t);
% H_t_diff = output_diff * (out_para') .* sigmoid_output_to_derivative(H_t);
H_t_diff = output_diff * (out_para') .* sigmoid_output_to_derivative(H_t);
% out_para_diff = output_diff * (H_t) * sigmoid_output_to_derivative(out_para);
out_para_diff = (H_t') * output_diff;
% out_gate diference
O_t_diff = H_t_diff .* tanh(C_t) .* sigmoid_output_to_derivative(O_t);
% C_t difference
C_t_diff = H_t_diff .* O_t .* tan_h_output_to_derivative(C_t);
% forget_gate_diffeence
F_t_diff = C_t_diff .* C_t_1 .* sigmoid_output_to_derivative(F_t);
% in_gate difference
I_t_diff = C_t_diff .* G_t .* sigmoid_output_to_derivative(I_t);
% g_gate difference
G_t_diff = C_t_diff .* I_t .* tan_h_output_to_derivative(G_t);
% differences of U_i and W_i
U_i_diff = X' * I_t_diff .* sigmoid_output_to_derivative(U_i);
W_i_diff = (H_t_1)' * I_t_diff .* sigmoid_output_to_derivative(W_i);
% differences of U_o and W_o
U_o_diff = X' * O_t_diff .* sigmoid_output_to_derivative(U_o);
W_o_diff = (H_t_1)' * O_t_diff .* sigmoid_output_to_derivative(W_o);
% differences of U_o and W_o
U_f_diff = X' * F_t_diff .* sigmoid_output_to_derivative(U_f);
W_f_diff = (H_t_1)' * F_t_diff .* sigmoid_output_to_derivative(W_f);
% differences of U_o and W_o
U_g_diff = X' * G_t_diff .* tan_h_output_to_derivative(U_g);
W_g_diff = (H_t_1)' * G_t_diff .* tan_h_output_to_derivative(W_g);
% update
U_i_update = U_i_update + U_i_diff;
W_i_update = W_i_update + W_i_diff;
U_o_update = U_o_update + U_o_diff;
W_o_update = W_o_update + W_o_diff;
U_f_update = U_f_update + U_f_diff;
W_f_update = W_f_update + W_f_diff;
U_g_update = U_g_update + U_g_diff;
W_g_update = W_g_update + W_g_diff;
out_para_update = out_para_update + out_para_diff;
end
U_i = U_i + U_i_update * alpha;
W_i = W_i + W_i_update * alpha;
U_o = U_o + U_o_update * alpha;
W_o = W_o + W_o_update * alpha;
U_f = U_f + U_f_update * alpha;
W_f = W_f + W_f_update * alpha;
U_g = U_g + U_g_update * alpha;
W_g = W_g + W_g_update * alpha;
out_para = out_para + out_para_update * alpha;
U_i_update = U_i_update * 0;
W_i_update = W_i_update * 0;
U_o_update = U_o_update * 0;
W_o_update = W_o_update * 0;
U_f_update = U_f_update * 0;
W_f_update = W_f_update * 0;
U_g_update = U_g_update * 0;
W_g_update = W_g_update * 0;
out_para_update = out_para_update * 0;
end
nn = newgrnn(train_x',train_y(:,1)',mean(mean(abs(out_para)))/2);4.操作步骤与仿真结论
通过本文的LSTM网络识别算法,对不同干扰大小采集得到的人脸进行识别,其识别正确率曲线如下图所示:
从图2的仿真结果可知,随着对采集图像干扰的减少,本文所研究的LSTM识别算法具有最好的识别准确率,RNN神经网络与基于卷积的深度神经网络,其识别率相当,普通的神经网络,其识别率性能明显较差。具体的识别率大小如下表所示:
表1 四种对比算法的识别率
| 算法 |
-15db |
-10db |
-5db |
0db |
5db |
10db |
15db |
| NN |
17.5250 |
30.9500 |
45.0000 |
52.6000 |
55.4750 |
57.5750 |
57.6000 |
| RBM |
19.4000 |
40.4500 |
58.4750 |
67.9500 |
70.4000 |
72.2750 |
71.8750 |
| RNN |
20.6750 |
41.1500 |
60.0750 |
68.6000 |
72.5500 |
73.3500 |
73.3500 |
| LSTM |
23.1000 |
46.3500 |
65.0250 |
72.9500 |
75.6000 |
76.1000 |
76.3250 |
5.参考文献
[01]米良川,杨子夫,李德升等.自动机器人视觉控制系统[J].工业控制计算机.2003.3.
[02]Or1ando,Fla.Digital Image Processing Techniques.Academic Pr,Inc.1984
[03]K.Fukushima.A neural network model for selective attention in visual pattern recognition. Biological Cybernetics[J]October 1986‑55(1):5-15.
[04]T.H.Hidebrandt Optimal Training of Thresholded Linear Correlation Classifiers[J]. IEEE Transaction Neural Networks.1991‑2(6):577-588.
[05]Van Ooyen B.Nienhuis Pattern Recognition in the Neocognitron Is Improved by Neural Adaption[J].Biological Cybernetics.1993,70:47-53.
[06]Bao Qing Li BaoXinLi. Building pattern classifiers using convolutional neural networks[J]. Neural.Networks‑vol.5(3): 3081-3085.
[07]E S ackinger‑,B boser,Y lecun‑,L jaclel. Application of the ANNA Neural Network Chip to High Speed Character Recognition[J]. IEEE Transactions on Neural Networks 1992.3:498-505.
A05-40
6.完整源码获得方式
方式1:微信或者QQ联系博主
方式2:订阅MATLAB/FPGA教程,免费获得教程案例以及任意2份完整源码