第十一届蓝桥杯Java B组真题及解析
分享今日花4个小时做的十一届的蓝桥杯试题。
算了一下得了90多分,可能是这一届的题比较简单。
第一题: 解密(5分)
题目描述
小明设计了一种文章加密的方法:对于每个字母 c,将它变成某个另外的字符 Tc。下表给出了字符变换的规则:
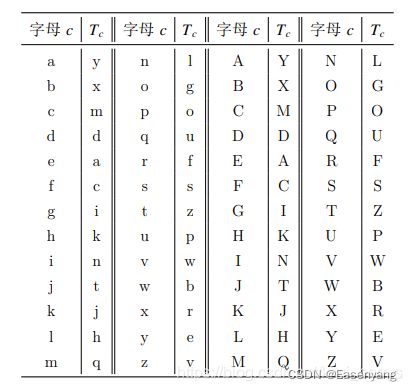
例如,将字符串 YeRi 加密可得字符串 EaFn。
小明有一个随机的字符串,加密后为
EaFnjISplhFviDhwFbEjRjfIBBkRyY
(由 30 个大小写英文字母组成,不包含换行符),请问原字符串是多少?
(如果你把以上字符串和表格复制到文本文件中,请务必检查复制的内容
是否与文档中的一致。在试题目录下有一个文件 str.txt,第一行为上面的字符
串,后面 52 行依次为表格中的内容。)
【答案提交】
这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
只包含 30 个大小写英文字母的字符串,在提交答案时只填写这个字符串,填写
多余的内容将无法得分。
答案: 直接一个一个地对应写出来就行(我居然错了,超小声)
YeRikGSunlRzgDlvRwYkXkrGWWhXaA
第二题:纪念日(5分)
题目描述
2020 年 7 月 1 日是中国共产党成立 99 周年纪念日。
中国共产党成立于 1921 年 7 月 23 日。
请问从 1921 年 7 月 23 日中午 12 时到 2020 年 7 月 1 日中午 12 时一共包含多少分钟?
【答案提交】
这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个
整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
答案:52038720
代码:
public class 纪念日 {
public static void main(String[] args) {
int day = 0;
int year = 2019-1921; // 先算中间有多少年,要把2020去掉,因为2020不满一年
day += year*365; // 算中间的天数,不算闰年的,闰年的下面处理
for (int i=1922;i<=2019;i++){
if ((i%4==0&&i%100!=0)||i%400==0) // 每有一个闰年则天数加一
day++;
}
day += 365-(31+28+31+30+31+30+23); // 加上1921年的天数
day += 31+29+31+30+31+30+1; // 加上2020年的天数
long min = day*24*60; // 计算分钟数
System.out.println(min);
}
}
第三题:: 合并检测(10分)
题目描述
新冠疫情由新冠病毒引起,最近在 A 国蔓延,为了尽快控制疫情,A 国准
备给大量民众进病毒核酸检测。
然而,用于检测的试剂盒紧缺。
为了解决这一困难,科学家想了一个办法:合并检测。即将从多个人(k个)采集的标本放到同一个试剂盒中进行检测。如果结果为阴性,则说明这 k个人都是阴性,用一个试剂盒完成了 k 个人的检测。如果结果为阳性,则说明至少有一个人为阳性,需要将这 k 个人的样本全部重新独立检测(从理论上看,如果检测前 k − 1 个人都是阴性可以推断出第 k 个人是阳性,但是在实际操作中不会利用此推断,而是将 k 个人独立检测),加上最开始的合并检测,一共使用了 k + 1 个试剂盒完成了 k 个人的检测。A 国估计被测的民众的感染率大概是 1%,呈均匀分布。请问 k 取多少能最节省试剂盒?
【答案提交】
这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
答案:10 (然后这题我也没做出来,看网上的答案才明白)
思路:因为感染率是1%,且均匀分布,我们可以假设只有100个人,那么感染的人为1,然后依次计算k的哪个取值最节省试剂。
代码:
public class 合并检测 {
public static void main(String[] args) {
int people = 100;
int min = Integer.MAX_VALUE;
int res = 0;
for (int k=1;k<=100;k++){
int temp;
if (people%k==0){ // 每一组人数相同的情况
temp = people/k+k;
}else temp = people/k+k+1; // 若有一组人数少,结果应加一,表示余数那一组
if (min>temp){
min = temp;
res = k;
}
}
System.out.print(res);
}
}
第四题:分配口罩(10分)
题目描述
某市市长获得了若干批口罩,每一批口罩的数目如下:(如果你把以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 mask.txt,内容与下面的文本相同)
9090400
8499400
5926800
8547000
4958200
4422600
5751200
4175600
6309600
5865200
6604400
4635000
10663400
8087200
4554000
现在市长要把口罩分配给市内的 2 所医院。由于物流限制,每一批口罩只能全部分配给其中一家医院。市长希望 2 所医院获得的口罩总数之差越小越好。请你计算这个差最小是多少?
【答案提交】
这是一道结果填空题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
答案:2400
思路:因为是填空题,我们可以按自己的方式去做,暴力都可以,我是用组合的方式求解,共15批口罩,必然一家7批,一家8批,那么我们就在15批中选7批(所有情况都考虑),然后计算两批的最小差值。
代码:
public class 分配口罩 {
static int[] num = new int[]{9090400,8499400,5926800,8547000,4958200,4422600,5751200,4175600,
6309600,5865200,6604400,4635000,10663400,8087200,4554000}; // 口罩数量
static long all = 0; // 口罩的总量,设置为全局变量方便访问
static long min = Long.MAX_VALUE; // 两家医院差的最小值
static boolean[] vis = new boolean[15]; // 是否已经分配
public static void main(String[] args) {
for (int i=0;i<15;i++){
all += num[i]; // 计算总量
}
solve(1);
System.out.println(min);
}
private static void solve(int k){ // 组合求解(跟求全排列很相似)
if (k>7){ // 若选了7批,则去比较两家医院的差值
min = Math.min(min,dec());
return;
}
for (int i=0;i<15;i++){
if (vis[i]) // 如果该批已选,就跳过
continue;
vis[i] = true;
solve(k+1);
vis[i] = false; // 回溯
}
}
private static long dec(){
long sumA = 0;
for (int i=0;i<15;i++){
if (vis[i]){
sumA += num[i]; // 计算已选的7批的和
}
}
long sumB = all-sumA; // 另一批的和就是总和减去已选的7批的和
return Math.abs(sumA-sumB); // 返回差值
}
}
第五题:斐波那契数列最大公约数(15分)
题目描述

答案:6765
思路:最开始我是用long型数组去存储各个值,但是精度不够,无法得到结果,然后我就换了刚接触的BigInteger,虽然不是很熟,但是有代码提示,很快就知道了各个函数的意思,得到了正解。
代码:
public class 斐波那契数列最大公约数 {
public static void main(String[] args) {
BigInteger[] arr = new BigInteger[2050]; // 创建数组来存储各个数值
arr[1] = BigInteger.ONE; // 初始化第一项和第二项为1
arr[2] = BigInteger.ONE;
for (int i=3;i<=2020;i++){
arr[i] = arr[i-1].add(arr[i-2]); // 利用公式来求解各个值
} // 它的加法是.add()
BigInteger gcd = arr[2020].gcd(arr[520]); // 求最大公约数的方法
System.out.println(gcd);
}
}
第六题:分类计数(15分)
题目描述
输入一个字符串,请输出这个字符串包含多少个大写字母,多少个小写字母,多少个数字。
【输入格式】
输入一行包含一个字符串。
【输出格式】
输出三行,每行一个整数,分别表示大写字母、小写字母和数字的个数。
【样例输入】
1+a=Aab
【样例输出】
1 3 1
【评测用例规模与约定】
对于所有评测用例,字符串由可见字符组成,长度不超过 100。
思路:直接用字符类contains方法来判断字符,若是大写字母、小写字母或数字,对应的计数就加一
代码:
public class 分类计数 {
static String Bigchar = "QWERTYUIOPASDFGHJKLZXCVBNM"; // 判断是否为大写字母的字符串
static String Smallchar = "qwertyuiopasdfghjklzxcvbnm"; // 判断是否为小写字母的字符串
static String number = "0123456789"; // 判断是否为数字的字符串
public static void main(String[] args) {
String s = new Scanner(System.in).nextLine();
int Bigsum = 0, Smallsum = 0, numsum=0; // 各个计数
for (int i=0;i<s.length();i++){
if (Bigchar.contains(s.charAt(i)+"")) // 逐个查看当前字符属于哪种字符
Bigsum++; // 对应的计数就加一
if (Smallchar.contains(s.charAt(i)+""))
Smallsum++;
if (number.contains(s.charAt(i)+""))
numsum++;
}
System.out.println(Bigsum+" "+Smallsum+" "+numsum);
}
}
【输入格式】
输入的第一行包含一个整数 n。
【输出格式】
输出一行,包含一个整数,表示答案。
【样例输入】
2
【样例输出】
257
【样例输入】
987654
【样例输出】
43636805
【评测用例规模与约定】
对于 20% 的评测用例,1 ≤ n ≤ 20。
对于 60% 的评测用例,1 ≤ n ≤ 1000。
对于所有评测用例,1 ≤ n ≤ 1000000。
思路:本题呢,跟第五题类似,也要用BigInteger来操作数据,解释在代码注释中。
代码:
public class 八次求和 {
public static void main(String[] args) {
int n = new Scanner(System.in).nextInt();
BigInteger bi = BigInteger.valueOf(n); // 初始化接收的数字
BigInteger b2 = solve(bi);
System.out.println(b2.mod(BigInteger.valueOf(123456789)));
}
private static BigInteger solve(BigInteger n){ // 求和函数
BigInteger temp = BigInteger.ZERO; // 存储和的变量
while (n.compareTo(BigInteger.ZERO) > 0){ // 这一行的意思是n>0就继续循环,直到n为0
temp = temp.add(n.pow(8)); // 累加
n = n.add(BigInteger.valueOf(-1)); // 这一句的意思是n=n-1,因为BigInteger没有相减的方法
} // 所以我们要加-1,控制循环次数
return temp;
}
}
第八题:字符串编码(20分)
题目描述
小明发明了一种给由全大写字母组成的字符串编码的方法。对于每一个大写字母,小明将它转换成它在 26 个英文字母中序号,即 A → 1, B → 2, … Z →26。这样一个字符串就能被转化成一个数字序列:比如 ABCXYZ → 123242526。现在给定一个转换后的数字序列,小明想还原出原本的字符串。当然这样的还原有可能存在多个符合条件的字符串。小明希望找出其中字典序最大的字
符串。
【输入格式】
一个数字序列。
【输出格式】
一个只包含大写字母的字符串,代表答案
【样例输入】
123242526
【样例输出】
LCXYZ
【评测用例规模与约定】
对于 20% 的评测用例,输入的长度不超过 20。
对于所有评测用例,输入的长度不超过 200000。
思路:转换方法是没问题的,本题注意点就是字典序最大,这样我们每次就要考虑每次组合出来的字母要选择大的,例如12我们就要选‘L’而不是‘A’和‘B’,这样就清楚了,从第一个数字开始,选择该位和连续的下一位,若小于等于26,就两位一起转换,不然就只能让该位的单独转换,下一位再和下下一位继续判断。
代码:
import java.util.Scanner;
public class 字符串编码 {
public static void main(String[] args) {
String s = new Scanner(System.in).nextLine();
char[] prc = new char[27]; // 存放1-26的转换规则
for (int i=1;i<=26;i++){
prc[i] = (char)('A'+ i - 1); // 定义转换规则
}
String res = solve(new StringBuilder(),s,prc,0); // 用StringBuilder来操作本题更方便
System.out.print(res);
}
private static String solve(StringBuilder sb, String s, char[] str, int k){
if (k>=s.length()) // 每一位都被转换了就结束
return sb.toString();
String a;
if (k==s.length()-1) // 若是最后一为,则这一位单独处理
a = s.charAt(k)+"";
else a = s.charAt(k)+""+s.charAt(k+1); // 若不是最后一位,则连续两位一起处理
int temp = Integer.parseInt(a); // 转化为int,方便查找转换规则
if (temp>26){
int n = Integer.parseInt(s.charAt(k)+""); // 若大于26,只能单独处理该位数字
sb.append(str[n]); // 把该位通过转换规则添加到StringBuilder
solve(sb,s,str,k+1); // 操作后一位
}else { // 若小于等于26,则连续两位一起处理
sb.append(str[temp]); // 通过转换规则加入StringBuilder
solve(sb,s,str,k+2); // 操作下下位(因为下一位已经处理了)
}
return sb.toString(); // 返回最终的字符串
}
}
第九题:BST 插入节点问题(25分)
题目描述
给定一棵包含 N 个节点的二叉树,节点编号是 1 ∼ N。其中 i 号节点具有权值 Wi,并且这些节点的权值恰好形成了一棵排序二叉树 (BST)。现在给定一个节点编号 K,小明想知道,在这 N 个权值以外,有多少个整数 X (即 X 不等于任何 Wi ) 满足:给编号为 K 的节点增加一个权值为 X 的子节点,仍可以得到一棵 BST。例如在下图中,括号外的数字表示编号、括号内的数字表示权值。编号1 ∼ 4 的节点权值依次是 0、10、20、30。
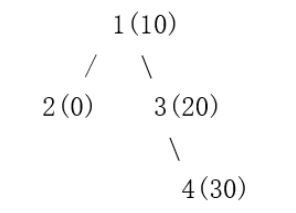
如果 K = 1,那么答案为 0。因为 1 号节点已经有左右子节点,不能再增加子节点了。
如果 K = 2,那么答案为无穷多。因为任何一个负数都可以作为 2 的左子节点。
如果 K = 3,那么答案为 9。因为 X = 11, 12, · · · , 19 都可以作为 3 的左子节点。
【输入格式】
第一行包含 2 个整数 N 和 K。
以下 N 行每行包含 2 个整数,其中第 i 行是编号为 i 的节点的父节点编号Pi 和权值 Wi 。注意 Pi = 0 表示 i 是根节点。输入保证是一棵 BST。
【输出格式】
一个整数代表答案。如果答案是无穷多,输出 −1。
【样例输入】
4 3
0 10
1 0
1 20
3 30
【样例输出】
9
【评测用例规模与约定】
对于 60% 的评测用例,1 ≤ K ≤ N ≤ 100,0 ≤ Wi ≤ 200,且 Wi 各不相同。
对于所有评测用例,1 ≤ K ≤ N ≤ 10000,0 ≤ Wi ≤ 100000000,且 Wi 各不相同。
答案:这题我不会做,后面参考了网上的代码再更新
第十题:网络分析(25分)
题目描述
小明正在做一个网络实验。他设置了 n 台电脑,称为节点,用于收发和存储数据。初始时,所有节点都是独立的,不存在任何连接。小明可以通过网线将两个节点连接起来,连接后两个节点就可以互相通信了。两个节点如果存在网线连接,称为相邻。小明有时会测试当时的网络,他会在某个节点发送一条信息,信息会发送到每个相邻的节点,之后这些节点又会转发到自己相邻的节点,直到所有直接或间接相邻的节点都收到了信息。所有发送和接收的节点都会将信息存储下来。一条信息只存储一次。给出小明连接和测试的过程,请计算出每个节点存储信息的大小。
【输入格式】
输入的第一行包含两个整数 n, m,分别表示节点数量和操作数量。节点从1 至 n 编号。接下来 m 行,每行三个整数,表示一个操作。如果操作为 1 a b,表示将节点 a 和节点 b 通过网线连接起来。当 a = b时,表示连接了一个自环,对网络没有实质影响。如果操作为 2 p t,表示在节点 p 上发送一条大小为 t 的信息。
【输出格式】
输出一行,包含 n 个整数,相邻整数之间用一个空格分割,依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。
【样例输入】
4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 1
【样例输出】
13 13 5 3
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ n ≤ 20,1 ≤ m ≤ 100。
对于 50% 的评测用例,1 ≤ n ≤ 100,1 ≤ m ≤ 1000。
对于 70% 的评测用例,1 ≤ n ≤ 1000,1 ≤ m ≤ 10000。
对于所有评测用例,1 ≤ n ≤ 10000,1 ≤ m ≤ 100000,1 ≤ t ≤ 100。
思路:就通过本题的逻辑,来一步步走下去,看操作数是‘1’还是‘2’,进行指定的操作,解释在代码注释中,需要注意的点是,它的m行操作是一行一行执行的,比如第n步的操作是发送信息,而n+1步是连接两个节点,若第n步是节点3发送信息5,n+1步是连接3和4,那么4的信息量不会改变,即不会加5.
代码:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.HashSet;
import java.util.Set;
public class 网络分析 {
static int[] node; // node数组是存放各节点存储信息的大小
static boolean[][] con; // con数组是判断i和j节点之间是否相邻
public static void main(String[] args) throws IOException { // 数据量有点大,可以考虑采用BufferedReader
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
String[] nm = reader.readLine().split(" ");
int n = Integer.parseInt(nm[0]); // 获取n和m
int m = Integer.parseInt(nm[1]);
node = new int[n+1];
con = new boolean[n+1][n+1];
for (int i=1;i<=m;i++){ // 该部分复杂度O(n平方)
String[] temp = reader.readLine().split(" "); // 获取每一行的操作
int a = Integer.parseInt(temp[1]);
int b = Integer.parseInt(temp[2]);
act(temp[0],a,b); // 执行操作 O(n)
}
for (int i=1;i<=n;i++)
System.out.print(node[i]+" "); // 输出结果
}
private static void act(String sign, int a, int b){ // 复杂度O(1)
switch (sign){
case "1":
connect(a,b); // 若第一位数是1,则将a和b相连
break;
case "2":
send(a,b); // 若第一位是2,则将a及它相连的各节点的存储信息大小都加b
}
}
private static void connect(int a,int b){ // 相连操作
con[a][b] = con[b][a] = true; // 先将a和b相连
for (int i=1;i<node.length;i++){ // 将其他与a和b相连的点变的相邻,方便操作
if (con[i][a]) // 因为相连的所有点都会接收到信息,所有直接让他们相邻
con[i][b]=con[b][i]=true;
if (con[i][b])
con[i][a]=con[a][i]=true; // 复杂度O(n)
}
for (int j=1;j<node.length;j++){
if (con[b][j])
con[a][j]=con[j][a]=true;
if (con[a][j])
con[b][j]=con[j][b]=true;
}
}
private static void send(int dot,int value){ // 发送信息操作
Set<Integer> set = new HashSet<>(); // HashSet来存放所有与它相邻的点,去掉重复的点
node[dot] += value;
for (int i=1;i<node.length;i++){ // 若相邻,则存入set
if (con[dot][i]&&i!=dot)
set.add(i);
}
for (int j=1;j<node.length;j++){ // 复杂度O(n)
if (con[j][dot]&&j!=dot)
set.add(j);
}
for (Integer k: set){
node[k] += value; // 所有相邻点的信息量都要加
}
}
}
由于蓝桥杯官网并没有这道题,不知道测试会不会超时,我看了一下复杂度是O(n平方),可能会超时,但通过70%应该是没问题的