目标检测算法(YOLOv4)

目标检测算法(YOLOv4)

本文要来介绍很火的目标检测算法YOLOv4，该算法是在原有YOLO目标检测架构的基础上，采用了近些年CNN领域中最优秀的优化策略，从数据处理、主干网络、网络训练、激活函数、损失函数等各个方面都有着不同程度的优化.

论文题目：YOLOv4: Optimal Speed and Accuracy of Object Detection

主要贡献

YOLOv4在YOLOv3上各个部分做改进,在保证速度的同时,大幅提高了模型的检测精度,并降低硬件使用的要求.

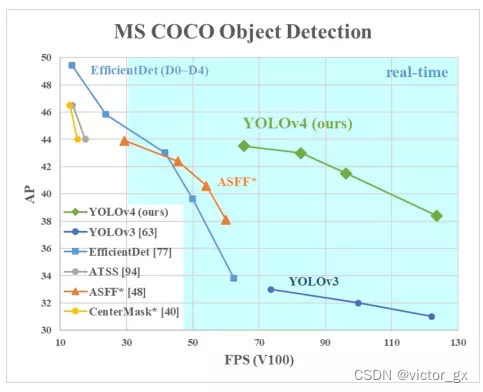
由上图可以看出:

• YOLOv4在MS COCO数据集上获得了43.5%的AP值(65.7% AP50).
• YOLOv4在与EfficientDet同等性能的情况下,速度是EfficientDet的两倍;
• 与YOLOv3相比,YOLOv4的AP和FPS分别提高了10%和12%.

该研究的主要贡献如下:

• 建立了一个强大高效的目标检测模型,并且使用1080TI或2080TI的GPU就可以进行训练
• 验证了SOTA的Bag-of-Freebies和Bag-of-Specials目标检测方法在检测器训练过程中的影响
• 改进了一些tricks,SOTA的方法,包括CBN,PAN,SAM等,使之更加高效,并你能够在单个GPU上训练

Tricks

Tricks一般指在网络训练和测试时所采用的技巧,在作者论文里将tricks分为两大类:Bag-of-Freebies 和 Bag-of-Specials.

Bag-of-Freebies是指在网络训练时所用到的技巧,不影响推理预测的时间,主要包括以下几个方面:

• 数据增强: Random erase, CutOut,Hide-and-seek,Grid mask,GAN,

  MixUp,CutMix

• 正则化方法: DropOut,DropConnect

• 处理数据不平衡问题: focal loss, Online hard example mining, hard negative example mining

• 处理预测框回归问题: MSE,IOU,GIOU,DIOU/CIOU

Bag-of-specials是指在网络设计或处理时所用到的技巧,轻微增加推理预测时间,但可以提升较大的精度,主要包括:

• 感受野: SPP,ASPP,RFB
• 特征融合: FPN,PAN
• 注意力机制: attention module
• 激活函数: Swish, Mish
• NMS: Soft-NMS,DIou NMS

网络结构

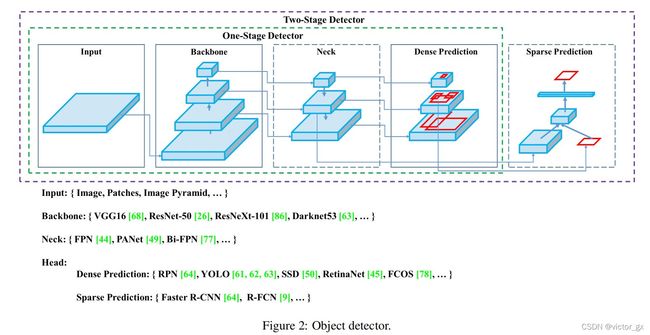
目标检测一般由以下几个部分组成:

• Input: 指图片的输入
• BackBone: 在ImageNet预训练的主干
• Neck:通常用来提取不同层级的特征图
• Head: 预测对象类别以及预测框的检测器,通常分为两类Dense Prediction(one stage)以及Sparse Prediction (two stage)

YOLOv4的模型架构由三部分组成:

• BackBone: CSPDarknet53
• Neck: SPP + PAN
• HEAD: YOLO HEAD

下面分别针对三个部分进行详细展开阐述.

BackBone–CSPDarknet53

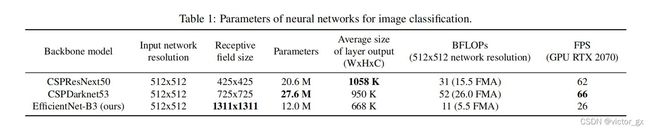
为了使网络能够快速操作并并行化优化,作者提供了两种神经网络主干

• 对于GPU,在卷积层中使用少量组(1-8group)的卷积,并将ResNeXt50,Darknet53分别与Cross Stage Partial Network(CSPNet)结合,组成了CSPResNeXt50和CSPDarknet53

由下表的实验证明CSPResNeXt50适合用于分类网络,而CSPDarknet53更适合用于检测网络,因此作者最后选择使用CSPDarknet53作为特征提取的主干

• 对于VPU,则使用了分组卷积(grouped-convolution),但不再使用Squeeze-and-excitement(SE)块,主要包括以下模型: EfficientNet-lite/MixNet/GhostNet/MobileNetV3

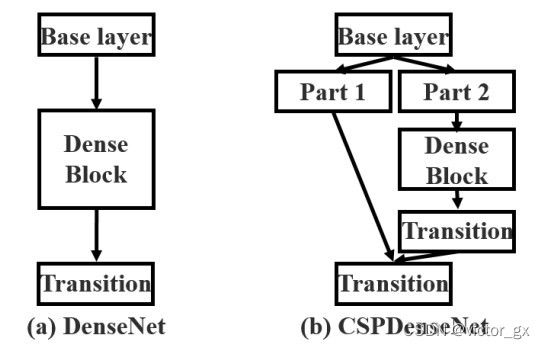
Cross Stage Partial Network (CSPNet)

在目标检测任务中通常是运行在小型设备上,因此需要计算量较低的模型,以缩短推理预测时间.CSPNet论文的作者认为预测计算量高的问题是由于网络优化中梯度信息重复导致,因此提出了跨阶段局部网络(CSPNet).

CSPNet的主要目的是使网络架构能够实现获取更丰富的梯度融合信息并降低计算量,作法是先将Base Layer的特征图划分为两个部分,然后在经过transition->concatenation->transition将两个部分融合起来.

上图中的Transition layer代表过度层,主要包含1X1卷积层以及pooling层.

上述作法使得CSPNet解决了三个问题:

• 增加CNN的学习能力,即便将模型轻量化,也能够保持准确性
• 去掉计算量较高的计算瓶颈结构
• 降低内存占用

上图为CSPNet结合不同的backbone后的结果,由上图中可以看出:

• 在ImageNet分类的准确率保持不变或是稍微提升一些,但是计算量却大幅下降.
• 在MS COCO检测的结果,CSPNet的AP50明显高于其他方法,并且在相同精度时,FPS要快很多.

Neck–SPP+PAN

Neck部分的主要作用在于能够扩大感受野以及融合不同尺度特征图的信息(更好的进行特征融合)

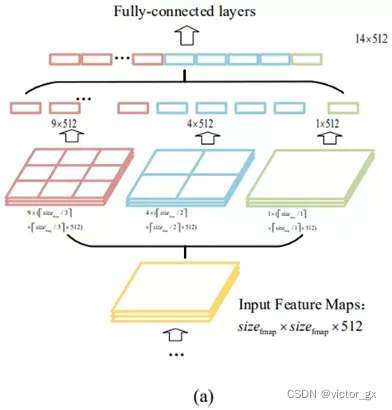
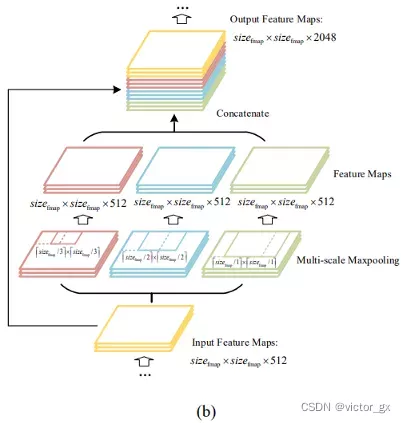
• SPP(Spatial Pyramid Pooling): 在网络的最后一层concat所有特征图,后面能够继续接CNN模块

下图a为YOLOv2的网络结构,将最后一层摊平后接上全链接层；图b则为使用SPP架构,将最后一层的特征图concat起来.

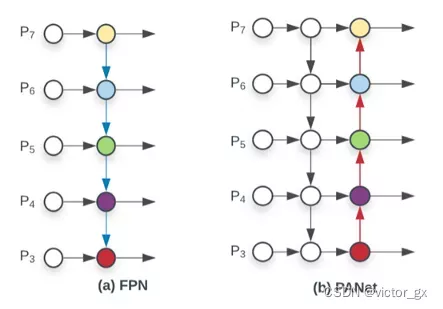
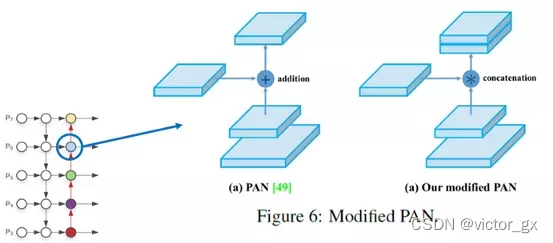
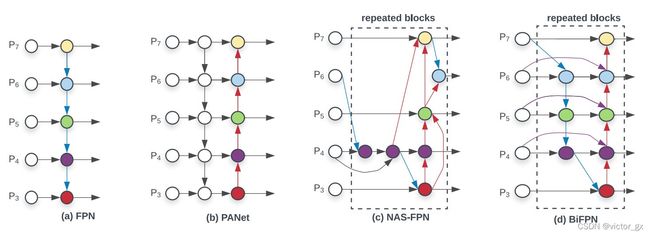
• PANet(Path Aggregation Network): 以FPN为基础进行改进,将串起来的层数再多加一层

另外还有将原本相加的部分修改为合并(concat),效果会比相加来的好,但是缺点就是通道数变多,计算量会变大.

HEAD–YOLO HEAD

YOLOv4的Head和YOLOv3的head部分一样,这里不再累述.

BOF and BOS

Bag-of-Freebies是指在网络训练时所用到的技巧,不影响推理预测的时间

Bag-of-Specials是指在网络设计或处理时所用到的技巧,轻微增加推理预测时间,但可以提升较大的精度

在对BOF和BOS进行详细展开之前,我们先来看一下YOLOv4所采用的完整方法有哪些:

接着我们对其中的每一项分别进行展开说明.

BoF for Backbone

CutMix

CutMix是2019年提出的数据增强的方式,

其核心思想是将一部分区域cut掉但不填充0像素而是随机填充训练集中的其他数据的区域像素值,分类结果按一定的比例分配.

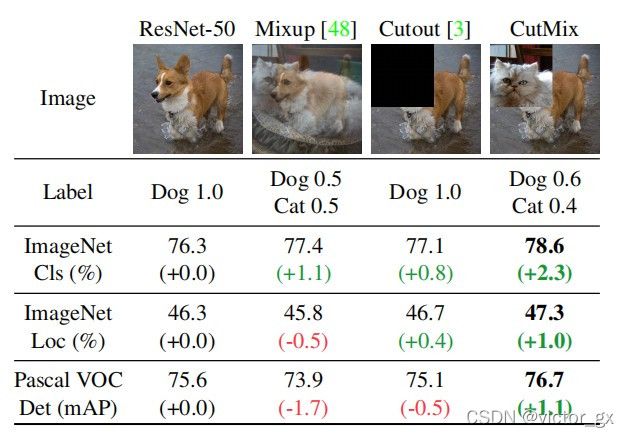
从下图中可以看出CutMix的Image以及Label是由两张不同的照片组合而成的,此外,数据增强还有另外两个方式: Mixup以及Cutout

• Mixup: 将随机的两张样本按比例混合,分类的结果按比例分配
• Cutout: 随机的将样本中的部分区域Cut掉,并且填充0像素值,分类的结果不变

Mosaic data augmentation

Mosaic 是作者新创的数据增强方法,采用随机缩放,裁剪的方式混合拼接4中图像进行训练,可以说是CutMix的加强版.

采用这种方法可以丰富检测数据集,并且因为随机缩放增加了很多小目标,让模型的稳健性更好.此外,作者考虑到可能需要只使用单个GPU的计算也能达到好的效果,因此使用Mosaic训练时,可以直接计算4张图片的数据,使得Mini-batch的大小不需要很大.

DropBlock regularizaton

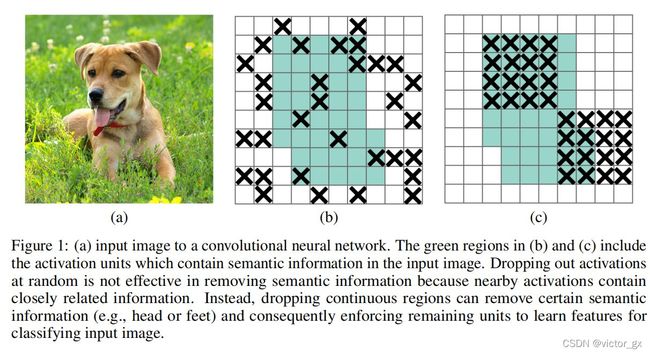
DropBlock与Dropout功能类似,也是避免overfitting的一种正则化方法,于2018年提出.

上图中,图b是使用Dropout的方法,会随机删除神经元的数量,但网络仍然可以从相邻的激活单元中学习到相同信息.

图c是使用DropBlock的方法,随机将整个局部区域进行删减,网络就会去注重学习某些特征以实现正确分类而得到更好的泛化效果.

Class Label smoothing

Label Smoothing 是图像分类经常会用到的一种正则化方法.

在分类任务中,通常会将输出用softmax进行归一化处理,再使用one-hot label去计算cross-entropy function来训练模型.但是使用one-hot向量表示容易导致网络overfitting的问题,因此Label Smoothing就是将one-hot label 变得更加soft, 使得计算loss时可以有效抑制overfitting的现象,提高模型的泛化能力.

具体做法如下图所示,降低正确类别的权重,另一方面提高错误类别的权重.
$$y_k^{LS}=y_k(1-\alpha )+\frac{\alpha }{K}$$
其中,K为类别数,为超参,在 为正确类别时为1,错误类别时为0

BoS for Backbone

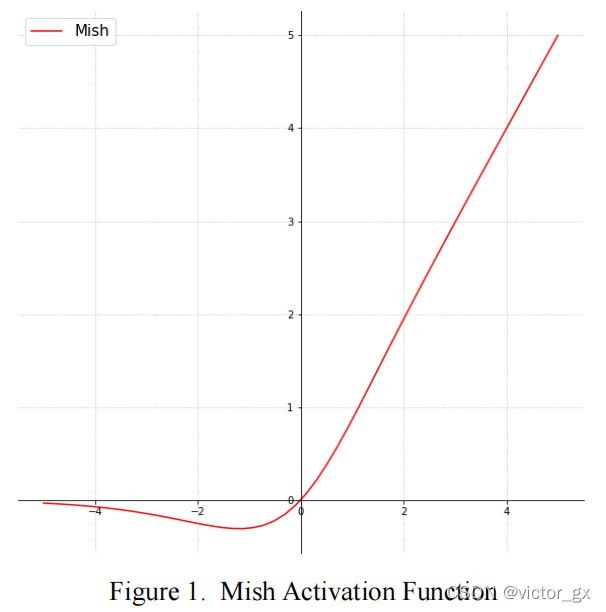
Mish activation

Mish是连续可微的非单调激活函数,跟ReLU相比,Mish的梯度更加平滑,并且在负值时允许有较小的负梯度,可以稳定网络的梯度流,具有更好的泛化能力.

公式定义如下:
$$f(x)=x\tanh (\ln (1+e^x))$$

YOLOv4作者使用CSPDarknet53网络在ImageNet数据集上做图像分类任务,发现使用了Mish激活函数的TOP-1和TOP-5的精度比没有使用时都略高一些.

因为YOLOv4的Backbone中都使用了Mish激活函数,而后面的网络层则还是使用leaky relu函数.

Multiinput weighted residual connections (MiWRC)

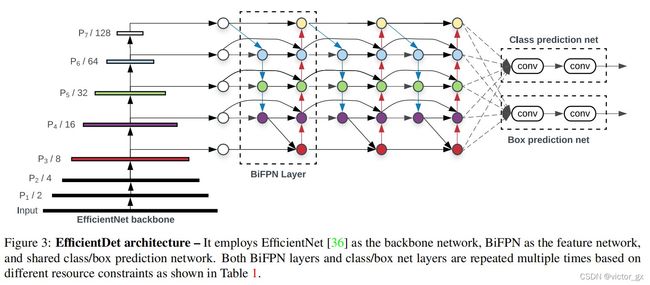
YOLOv4参考了EfficientDet的架构以及方式,使用了多输入加权的残差链接(MiWRC)作为backbone的BOS.

• EfficientDet的backbone使用EfficientNet, Neck为BiFPN

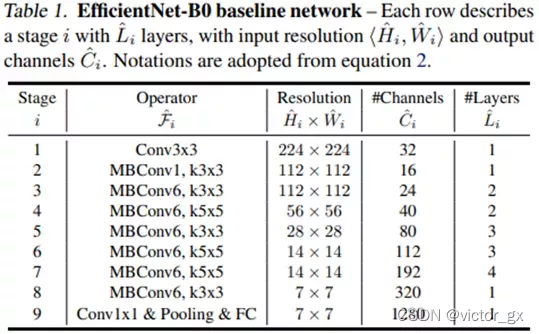
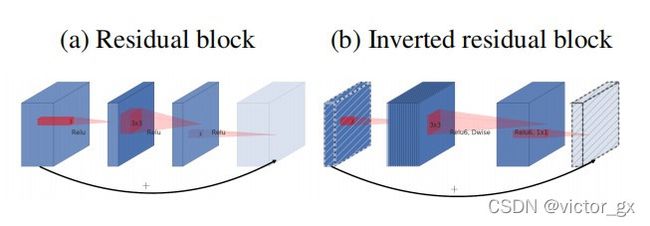
由下图可以看出EfficientNet-B0的架构通过多个MBConv Block构成,MBConv Block就是指MobileNet V2的Inverted Residual Block.

MBConv的主要架构如下右图所示,其设计是先升维再降维,与residual block先降维在升维的操作不同,而这样的设计可以让MobileNet v2能够更好的利用残差连接以提升准确率.

BiFPN是由PANet进行进化,删除贡献程度小的节点,并提出跨尺度融合的优化方法,在输入与输出结点中间加入connection.

MiWRC的思想源自于BiFPN,在FPN中每一层取得的feature都视为平等的,而MiWRC则认为不同层的feature理应有不同的重要性,需针对不同尺度的特征给予不同的权重比例.

BoF for detector

CIOU-Loss

在介绍CIOU-loss之前,先说明IOU loss的缺点以及各个IOU loss的演进过程, 框回归loss进化过程如下:

Smooth L1 Loss -> IOU Loss(2016) -> GIOU Loss(2019) -> DIOU Loss(2020) -> CIoU Loss(2020)

接下来对上述loss进行展开说明.

IOU Loss

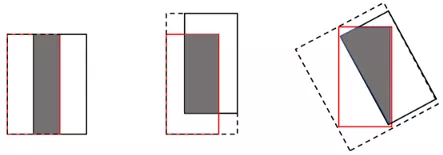
使用IOU Loss会有两个问题:

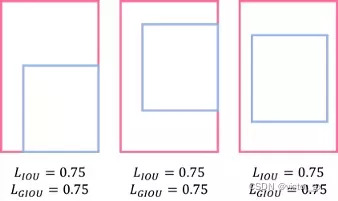
• 当预测框和目标框不相交时,IOU为0,无法反映两个框之间的远近,此时损失函数不可导,也就是说无法计算梯度,因此无法优化两个框不相交的情况
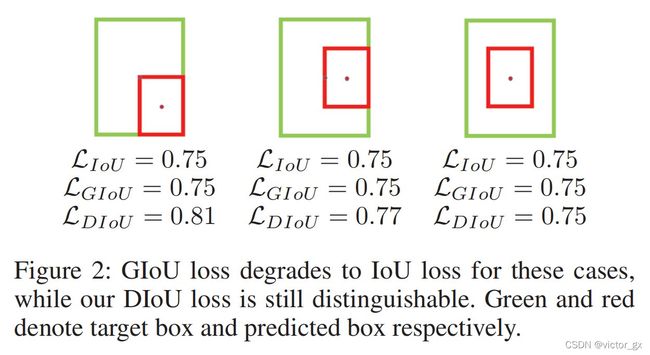
• IOU无法反映预测框与目标框的重合大小,如下图所示,这三种情况拥有相同的IOU值,但是重合度不同

之后的GIoU,DIoU,CIoU都是基于IOU loss增加一个惩罚项:
$$\begin{gathered} L_{IOU}=1-IOU \\ L=1-IOU+R(B,B^{gt}) \end{gathered}$$

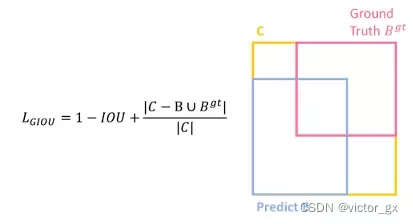
GIOU Loss (Generalized IOU Loss)

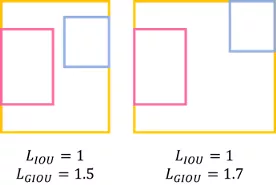
GIOU 为了解决预测框与目标框不重叠的问题,因此在IOU loss的基础上增加一个惩罚项,比IOU 更能反映两个框的接近程度.

由上图可以看到C为目标框Ground Truth与预测框Predict的最小包围框

由上图可以得知,当两个框距离越远,GIOU loss越大,因此GIOU 相比IOU更能反映两个框的接近程度.

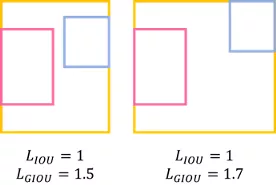
虽然GIOU解决了IOU的梯度问题,但是仍存在一些缺点…

• 在训练过程中,GIOU会倾向于先增大predict bounding box的大小,使它能够与gt有所重叠,如此一来才能计算IOU loss.这个操作会导致消耗大量的时间,影响模型收敛速度.
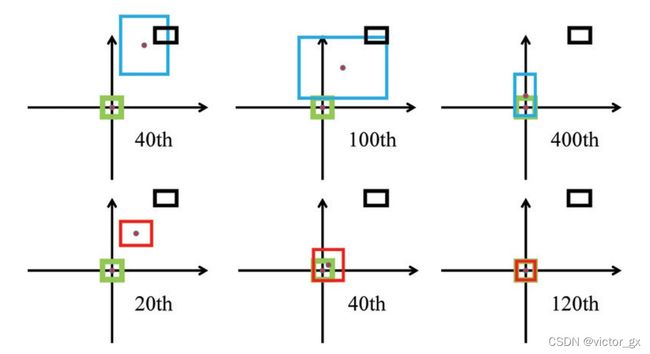
• 由下图可以看到predict bounding box的变化过程,绿色框为目标框的gt,黑色框为anchor box,蓝色框为预测框predict bounding box.

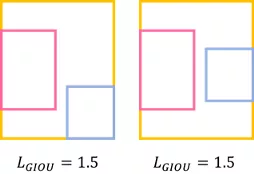
• 若预测框刚好在目标框内部时,此时GIOU loss 与 IOU loss的值一样,无法区分相对位置,如下图所示:

• 当两个框平行或者垂直时,会导致GIOU loss的值一样

DIOU Loss (Distance IOU Loss)

基于IOU与GIOU存在的问题,作者提出了两个问题:

• 直接最小化预测框与目标框之间归一化距离是否可行,以达到更快的收敛速度
• 如何在预测框与目标框有重叠时,回归地更准确

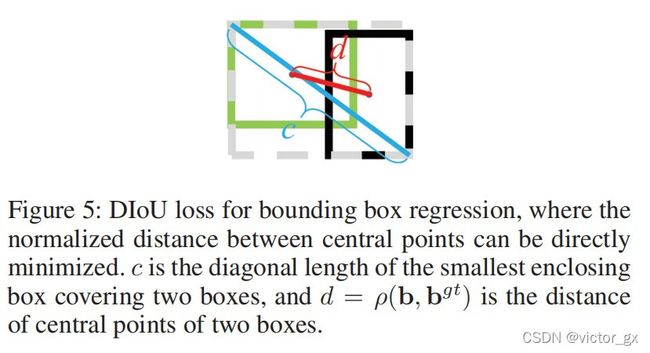
DIOU考虑了重叠面积与中心点的距离,增加了一个惩罚项用于最小化两个框的中心点距离
$$\begin{gathered} L_{DIOU}=1-IOU+\frac{{\rho }^2(b,b^{gt})}{c^2} \\ b,b^{gt}分别表示B,B^{gt}的中心点, \\ \rho 是欧式距离, \\ c是最小距离包围两个框的对角线长度 \end{gathered}$$

DIOU loss的优点为:

• DIOU 能够直接优化两个框之间的距离,而GIOU趋向减少最小包围框的面积,因此比GIOU loss收敛速度更快.如下图所示:

当预测框在目标框内部时,GIOU loss 与IOU loss的值相同,此时GIOU退化成IOU而无法区分其相对位置,DIOU可以更好地优化此类问题.如下所示:

可以将DIOU替换IOU用于计算NMS算法中,即论文中提出的DIOU-NMS

CIOU Loss (Complete IOU Loss)

一个好的目标框损失损失函数应考虑三个因素:重叠面积,中心点距离,长宽比,DIOU loss考虑了重叠面积与中心点距离,但没有考虑长宽比,因此作者提出了CIOU loss将三个因素都考虑到,并且模型的收敛精度更高.

CIOU在DIOU的基础上多增加了一个惩罚项,考虑了长宽比的因素.公式如下:
$$\begin{gathered} L_{CIOU}=1-IOU+\frac{{\rho }^2(b,b^{gt})}{c^2}+\alpha \nu , \\ \nu =\frac{4}{{\pi }^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h}{)}^2, \\ \alpha =\frac{\nu }{(1-IOU)+\nu } \\ b,b^{gt}分别表示B,B^{gt}的中心点, \\ \rho 是欧式距离, \\ c是最小距离包围两个框的对角线长度, \\ \alpha 是权重函数,依据两个框之间的距离来调整, \\ \nu 是衡量长宽比的相似性 \end{gathered}$$
CIOU loss的梯度类似于DIOU loss,但是要考虑v的梯度,以下是v的梯度计算公式:
$$\begin{gathered} \frac{\partial \nu }{\partial w}=\frac{8}{{\pi }^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h})\ast \frac{h}{w^2+h^2}, \\ \frac{\partial \nu }{\partial h}=-\frac{8}{{\pi }^2}(arctan\frac{w^{gt}}{h^{gt}}-arctan\frac{w}{h})\ast \frac{h}{w^2+h^2} \end{gathered}$$
$w^2+h^2$在这种情况下通常是一个小值 $h$和$w$在[0,1]范围内,可能产生梯度爆炸. 因此在我们的实现中,为了稳定收敛,简单地去除$w^2+h^2$ 将步长$\frac{1}{w^2+h^2}$替换为1,梯度方向仍然与等式一致

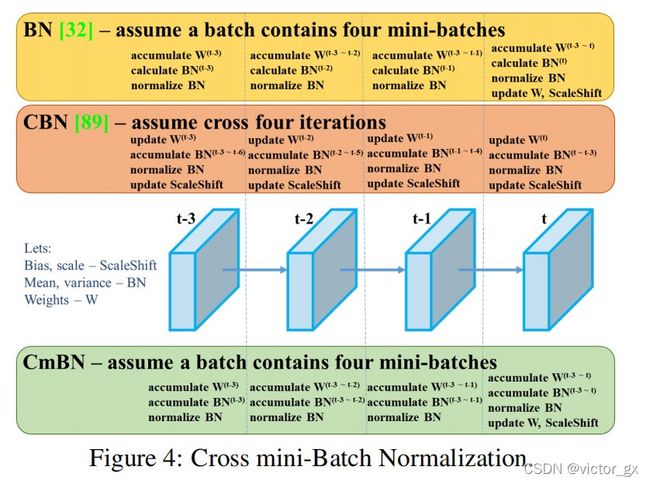
CmBN (Cross mini-Batch Normalization)

下图表示三种不同的BN方式:

• BN是对当前mini-batch进行归一化,但往往batch size都很小,可能会发生抽样不均匀而导致归一化会有问题,因此有很多对于小batch size的 BN方法.
• CBN的想法就是将之前mini-batch一起计算,但不保留太多个mini-btach,做法是对当前及当前3个mini-batch的结果进行归一化
• YOLOv4新创的CmBN是基于CBN去做修改,在mini-batch之间不做更新计算,而是在一个batch做完后才去更新网络参数.

SAT (self-Adversarial Training)

SAT是作者创新的一种数据增强的方法,分成两个阶段完成:

• 首先,先对训练样本进行前向传播,然后进行反向传播时修改图片像素(不修改网络权重),降低模型检测性能,通过这种方式让神经网络对自身执行对抗式学习,制造出图片没有检测对象的错觉.这一阶段其实就是在在增加样本的训练难度.
• 第二阶段,就是使用这些修改过的图片对模型进行训练

上述训练方式有助于推广模型和降低模型过拟合问题.

Eliminate grid sensitivity

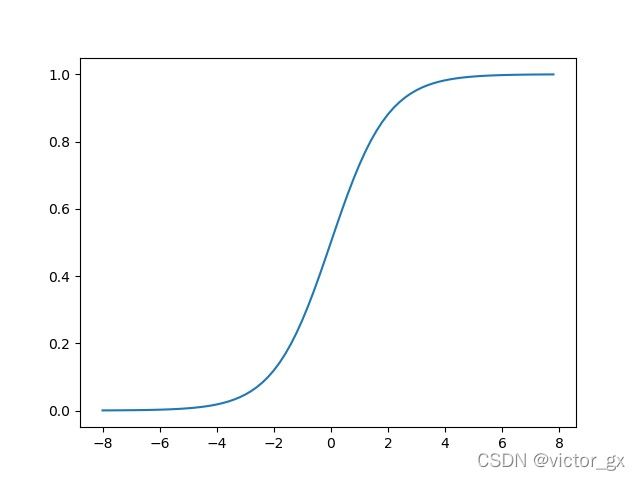
作者在观测一段物体检测的影片中发现,因为检测物体的中心点多位于接近Grid中心,而导致在Grid边缘时较难检测,但实际状况物体移动的路线是连续的,所以其中心位置应该也是连续的,也就是说物体可能会出现在Grid边缘.

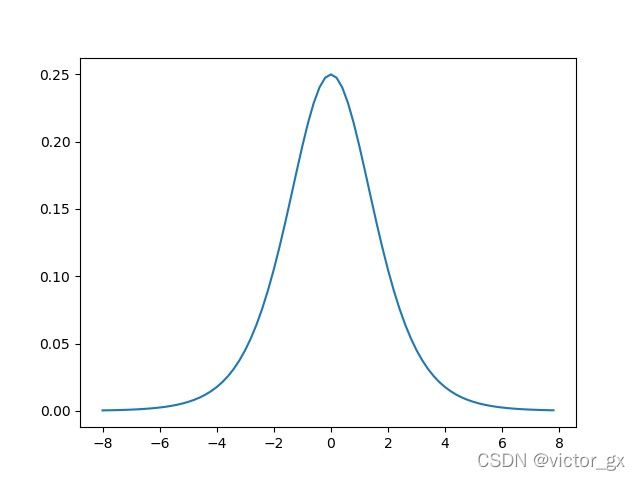
作者认为之所以有检测物体的中心点多位于接近Grid中心点的问题存在,是因为Sigmoid函数的梯度,由下图可以看到Sigmoid在Grid边缘时倒数接近0,容易发生梯度消失,导致中心点在Grid边缘时很难学习到准确的结果.

Sigmoid

Sigmoid导数

因此作者在Sigmoid函数做了些改变,将Sigmoid乘以一个大于1的值,并且考虑到不同的Grid Size对于边界效应的敏感度,采用 $(1+x)\ast Sigmoid-(0.5\ast x)$

Cosine annelaling 是利用余弦函数来调整学习率,一开始会先缓慢的降低学习率,然后中途在加速下降,最后再次缓慢下降.

Pytorch提供了两个版本的Cosine annealing

torch.optim.lr_scheduler.CosineAnnealingLR (optimizer, T_max, eta_min=0, last_epoch=-1, verbose=False)

• optimizere 指优化器
• T_max是指最大的迭代次数,表示cos周期的1/4
• eta_min是指最小学习率
• last_epoch是指最后一个epoch的索引,默认为-1
• verbose表示是否要印出更新的消息

公式如下:
$$\begin{gathered} {\eta }_t={\eta }_{min}+\frac{1}{2}({\eta }_{max}-{\eta }_{min})(1+cos(\frac{T_{cur}}{T_{max}}\pi )) \\ {\eta }_t是指learningrate, \\ {\eta }_{max}是指最大learningrate, \\ {\eta }_{min}是指最小learningrate, \\ {T}_{cur}是指当前迭代次数, \\ {T}_{max}是指最大迭代次数 \end{gathered}$$

torch.optim.lr_scheduler.CosineAnnealingWarmRestarts (optimizer, T_0, T_mult=1, eta_min=0, last_epoch=-1, verbose=False)

它与CosinAnnealingLR()参数有两个不一样的地方:

• optimizere 指优化器

• T_0是指第一次重新启动的迭代次数

• T_mult是指一个因子在重新启动后增加$T_i$,默认值:1

• eta_min是指最小学习率,默认为0

• last_epoch是指最后一个epoch的索引,默认为-1

• verbose表示是否要印出更新的消息

公式如下:
$$\begin{gathered} {\eta }_t={\eta }_{min}+\frac{1}{2}({\eta }_{max}-{\eta }_{min})(1+cos(\frac{T_{cur}}{T_i}\pi )) \\ {\eta }_t是指learningrate, \\ {\eta }_{max}是指最大learningrate, \\ {\eta }_{min}是指最小learningrate, \\ {T}_{cur}是指重新启动后的迭代次数, \\ {T}_{max}是指第i轮的迭代次数 \end{gathered}$$

Optimal hyperparameters

使用基因算法Genetic Algorithms来选择超参数.作法是先随机组合超参数去做训练,然后挑选出最好的10%超参数再去随机组合并训练,最后选择最佳的模型.

BoS for detector

SAM-block

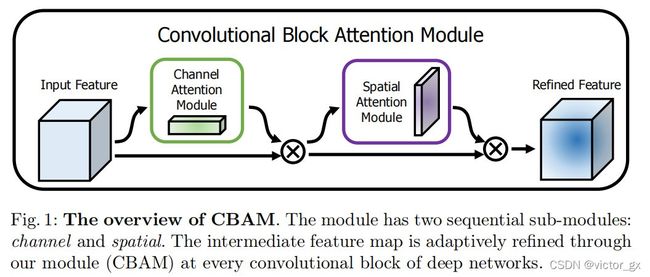
SAM源自于论文CBAM(Convolutional Block Attention Module)的论文,提出了两种注意力机制的技巧.

• 先来介绍一下CBAM,如下图所示,输入一个特征F,先进行Channel attention module后得到权重系数和原来的特征F相乘,然后在进行Spatial attention module后得到权重系数和原来的特征F相乘,最后就可以得到缩放后的新特征.

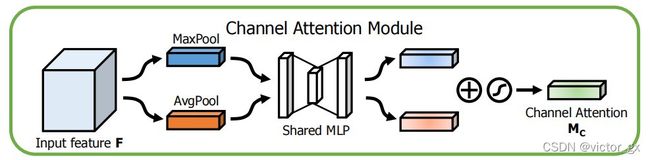
• 接着我们来介绍Channel attention module(通道注意力模块),该模块就是将输入的特征F分别进行全局的Maxpooling与Averagepooling,接着将这两个输入到一个权重共享的MLP,再将这两个进行element-wise summation操作后经过Sigmoid函数会得到权重系数Mc,再将这个权重系数与原来的特征F相乘,就可以得到缩放后的新特征.

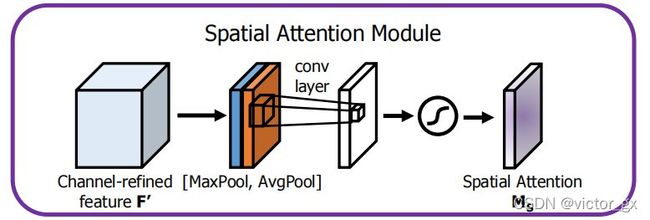
• Spatial attention module(空间注意力模块), 首先对不同的feature map上相同位置的像素值进行全局的Maxpooling与Average pooling,接着将这两个spatial attention map 进行concat, 再利用一个7X7的卷积后经过Sigmoid函数会得到权重系数Ms,在将这个权重系数与原来的特征F相乘,就可以得到缩放后的新特征,如下所示:

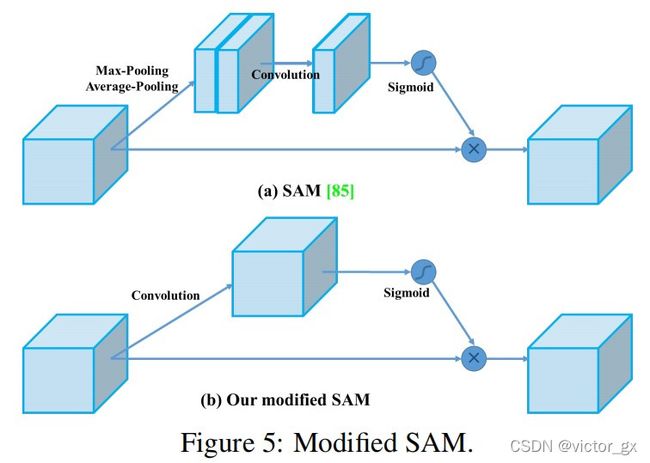
• YOLOv4将SAM修改为pointwise attention,由下图可以看到它不做Maxpooling 与Average pooling的操作,而是直接接一个7X7的卷积层,如下:

DIOU-NMS

在经典的NMS中,置信度最高的检测框和其他检测框会逐一算出对应的IOU值,并将值超过阈值的检测框过滤掉.但是在实际情况下,当两个不同的物体靠的很近时,由于IOU值比较大,在经过NMS算法后,往往只剩下一个检测框,这样容易导致有漏检的状况发生.

• DIOU-NMS不仅考虑IOU的值,还考虑两个框的中心点的距离.如果两个框之间的IOU比较大,但是他们中心点之间的距离比较远,则会被认为是不同物体的检测框而不会被过滤掉.

以下是DIOU-NMS的公式:
$$\begin{gathered} s_i=\{\begin{array}{l}{s}_i,IOU-R_{DIOU}(M,B_i)<\epsilon \\ 0,IOU-R_{DIOU}(M,B_i)\ge \epsilon ,\end{array} \\ {s}_i为分类置信度, \\ \epsilon 为NMSthreshold, \\ M为最高置信度的检测框 \end{gathered}$$
解释:

• 得分最高的预测框M和其他框 的DIOU值比IOU值大时, 的置信度仍可以保持;反之,就将 的置信度设置为0