python最大堆heapq_Python-堆的实现与heapq(最小堆库函数)
目录
简介
堆是一个二叉树,它的每个父节点的值都只会小于或大于所有孩子节点(的值)。它使用了数组来实现:从零开始计数,对于所有的 k ,都有 heap[k] <= heap[2*k+1] 和 heap[k] <= heap[2*k+2]。 为了便于比较,不存在的元素被认为是无限大。 堆最有趣的特性在于最小的元素总是在根结点:heap[0]。类似于C++的优先队列。
heapq
创建
heapq.heapify(x)
将list x 转换成堆,原地,线性时间内。
>>> from heapq import *
>>> heap = [2,7,4,1,8,1]
>>> heapify(heap)
>>> print(type(heap),heap)
[1, 1, 2, 7, 8, 4]
添加
heappush(heap, item)
将 item 的值加入 heap 中,保持堆的不变性。
>>> heappush(heap,9)
>>> print(heap)
[1, 1, 2, 7, 8, 4, 9]
删除
heappop(heap)
弹出并返回 heap 的最小的元素,保持堆的不变性。如果堆为空,抛出IndexError。使用 heap[0] ,可以只访问最小的元素而不弹出它。
>>> heappop(heap)
1
>>> print(heap)
[1, 7, 2, 9, 8, 4]
高效增删
heappushpop(heap, item)
将 item 放入堆中,然后弹出并返回 heap 的最小元素。该组合操作比先调用heappush()再调用heappop()运行起来更有效率。
>>> heappushpop(heap,9)
1
>>> print(heap)
[2, 7, 4, 9, 8, 9]
heapreplace(heap, item)
弹出并返回 heap 中最小的一项,同时推入新的 item。 堆的大小不变。 如果堆为空则引发IndexError。
这个单步骤操作比heappop()加heappush()更高效,并且在使用固定大小的堆时更为适宜。 pop/push 组合总是会从堆中返回一个元素并将其替换为 item。
返回的值可能会比添加的 item 更大。 如果不希望如此,可考虑改用heappushpop()。 它的 push/pop 组合会返回两个值中较小的一个,将较大的值留在堆中。
堆的实现
堆的特点:
内部数据是有序的
可以弹出堆顶的元素,大根堆就是弹出最大值,小根堆就是弹出最小值
每次加入新元素或者弹出堆顶元素后,调整堆使之重新有序,时间复杂度O(logn)
堆的本质:
它是一个完全二叉树
实现的时候不需要建造一个树,改用一个数组即可
一直一个节点的索引为index,那么,父节点的索引为
![]() ,左孩子节点编号为index*2+1,右孩子节点为index*2+2
,左孩子节点编号为index*2+1,右孩子节点为index*2+2
树
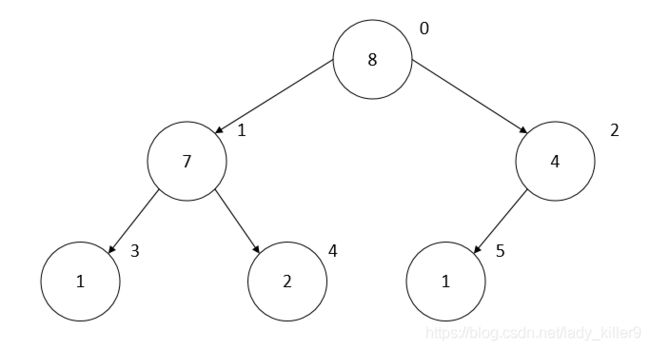
以序列2,7,4,1,8,1为例,最后形成的二叉树如上图所示,列表见下表
堆对应的实际列表元素874121
下标012345
添加
元素放入列表尾
列表尾元素向上调整,和父节点交换,直到当前元素不符合交换条件(大根堆时就是大于父节点需要调整,小根堆反之)
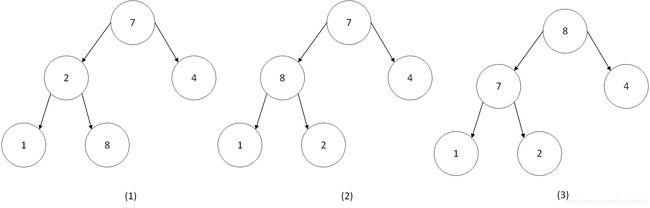
插入8的过程
以插入8为例,8插入到列表末尾,列表为7 2 4 1 8,之后8与2比较后交换,改为7 8 4 1 2,之后8与7比较后交换,改为8 7 4 1 2,结束。
删除
交换堆顶元素与末尾元素
删除列表末尾元素
新的堆顶元素向下调整,和子节点交换,直到当前元素不符合条件(大根堆时就是小于子节点(选择更大的子节点)需要调整,小根堆反之)
初始化
def __init__(self, desc=True):
"""
init a heap, default big root heap
:param desc:True,big root heap;False, little root heap.
"""
self.heap = []
self.desc = desc
初始化一个大根堆
参数
desc:降序,默认为True
大小
@property
def size(self):
"""
:return: size of heap
"""
return len(self.heap)
返回
堆的大小,即列表长度
得到堆顶
def top(self):
"""
get top of heap
:return: the top of heap
"""
try:
return self.heap[0]
except Exception:
raise IndexError('heap is empty.')
返回
堆顶元素,如果堆为空,引发IndexError。
添加
def push(self, val):
"""
add an element to heap
:param val: the value of element
:return: None
"""
self.heap.append(val)
self._to_up(self.size - 1)
return None
把元素添加到尾部,再向上调整
参数
val:待添加元素的值
_to_up:向上调整
def _to_up(self, index):
"""
adjust bottom one to up
:param index:size of heap - 1
:return: None
"""
while index:
parent = (index - 1) // 2
if self._better(self.heap[parent], self.heap[index]):
break
self.heap[parent], self.heap[index] = self.heap[index], self.heap[parent]
index = parent
return None
尾部元素调整到上面
参数
index:长度-1
def _better(self, node1, node2):
return node1 > node2 if self.desc else node1 < node2
选择一个符合条件的,根据desc来判断
删除
def pop(self):
"""
delete the top of heap
:return:the top of heap
"""
item = self.heap[0]
self.heap[0], self.heap[-1] = self.heap[-1], self.heap[0]
self.heap.pop()
self._to_down(0)
return item
删除堆顶元素
返回
堆顶元素
def _to_down(self, index):
"""
adjust top one to down
:param index: 0
:return: None
"""
while index * 2 + 1 < self.size:
best = index
left = index * 2 + 1
right = index * 2 + 2
if self._better(self.heap[left], self.heap[best]):
best = left
if right < self.size and self._better(self.heap[right], self.heap[best]):
best = right
if best == index:
break
self.heap[index], self.heap[best] = self.heap[best], self.heap[index]
index = best
return None
以大根堆为例
判断是否存在左孩子
若存在,找出当前节点和左孩子中更大的
判断是否存在右孩子
若存在,找出当前节点和右孩子中更大的
若当前节点是最大的,不变,否则,交换当前节点和最大的
参数
index:0
结果截图
全部代码
"""
--coding:utf-8--
@File: heap.py.py
@Author:frank yu
@DateTime: 2020.12.31 11:15
@Contact: [email protected]
@Description:
"""
class Heap:
def __init__(self, desc=True):
"""
init a heap, default big root heap
:param desc:True,big root heap;False, little root heap.
"""
self.heap = []
self.desc = desc
@property
def size(self):
"""
:return: size of heap
"""
return len(self.heap)
def top(self):
"""
get top of heap
:return: the top of heap
"""
try:
return self.heap[0]
except Exception:
raise IndexError('heap is empty.')
def push(self, val):
"""
add an element to heap
:param val: the value of element
:return: None
"""
self.heap.append(val)
self._to_up(self.size - 1)
return None
def pop(self):
"""
delete the top of heap
:return:the top of heap
"""
item = self.heap[0]
self.heap[0], self.heap[-1] = self.heap[-1], self.heap[0]
self.heap.pop()
self._to_down(0)
return item
def _better(self, node1, node2):
return node1 > node2 if self.desc else node1 < node2
def _to_up(self, index):
"""
adjust bottom one to up
:param index:size of heap - 1
:return: None
"""
while index:
parent = (index - 1) // 2
if self._better(self.heap[parent], self.heap[index]):
break
self.heap[parent], self.heap[index] = self.heap[index], self.heap[parent]
index = parent
return None
def _to_down(self, index):
"""
adjust top one to down
:param index: 0
:return: None
"""
while index * 2 + 1 < self.size:
best = index
left = index * 2 + 1
right = index * 2 + 2
if self._better(self.heap[left], self.heap[best]):
best = left
if right < self.size and self._better(self.heap[right], self.heap[best]):
best = right
if best == index:
break
self.heap[index], self.heap[best] = self.heap[best], self.heap[index]
index = best
return None
def create(self, seq):
for val in seq:
self.push(val)
return None
def menu():
print('--------------------Menu--------------------')
print('1.Create 2.Push')
print('3.Pop 4.Top')
print('5.Size')
print('e.Exit')
if __name__ == '__main__':
seq = input('please enter a sequence separated by white space:')
# use seq to create a big root heap
heap = Heap()
heap.create(seq.split())
while True:
menu()
choice = input('please select an option:')
if choice == 'e':
break
if choice == '1':
seq = input('please enter a sequence separated by white space:')
heap.create(seq.split())
elif choice == '2':
val = input('please enter a value:')
heap.push(val)
print(f'{val} has insert into heap.')
elif choice == '3':
val = heap.pop()
print(f'{val} has been deleted.')
elif choice == '4':
val = heap.top()
print(f'the top of heap is {val}.')
elif choice == '5':
size = heap.size
print(f'the size of heap is {size}.')
else:
print('something wrong, check your input.')
有问题请下方评论,转载请注明出处,并附有原文链接,谢谢!如有侵权,请及时联系。如果您感觉有所收获,自愿打赏,可选择支付宝18833895206(小于),您的支持是我不断更新的动力。