第十届蓝桥杯 2019年省赛真题 (Java 大学A组)
蓝桥杯 2019年省赛真题(Java 大学 A 组 )
- #A 平方和
- #B 数列求值
- #C 迷宫
- #D 最大降雨量
- #E RSA 解密
-
- Pollard's Rho
- #F 完全二叉树的权值
- #G 外卖店优先级
- #H 修改数组
-
- 并查集
- 树状数组上倍增
- #I 糖果
-
- 状压 DP
- #J 组合数问题
-
- Lucas 定理
打发时间。
#A 平方和
本题总分: 5 5 5 分
问题描述
小明对数位中含有 2 、 0 、 1 、 9 2、0、1、9 2、0、1、9 的数字很感兴趣,在 1 1 1 到 40 40 40 中这样的数包括 1 、 2 、 9 、 10 1、2、9、10 1、2、9、10 至 32 、 39 32、39 32、39 和 40 40 40,共 28 28 28 个,他们的和是 574 574 574,平方和是 14362 14362 14362。
注意,平方和是指将每个数分别平方后求和。
请问,在 1 1 1 到 2019 2019 2019 中,所有这样的数的平方和是多少?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
2658417853
public class Test {
public static void main(String[] args) { new Test().run(); }
int N = 2019;
long ans;
void run() {
for (int i = 1; i <= N; ++i)
if (check(i)) ans += i * i;
System.out.println(ans);
}
boolean check(int n) {
while (n > 0)
switch (n % 10) {
case 2:
case 0:
case 1:
case 9: return true;
default: n /= 10;
}
return false;
}
}
容易注意到 900 900 900 至 2019 2019 2019 都是小明感兴趣的数字,简单使用数列求和公式估值后,使用 i n t \mathrm{int} int 显然会溢出,因此改用长整形。
再没啥好说的。
#B 数列求值
本题总分: 5 5 5 分
问题描述
给定数列 1 , 1 , 1 , 3 , 5 , 9 , 17 , ⋯ 1, 1, 1, 3, 5, 9, 17, \cdots 1,1,1,3,5,9,17,⋯,从第 4 4 4 项开始,每项都是前 3 3 3 项的和。求第 20190324 20190324 20190324 项的最后 4 4 4 位数字。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
4659
朴素解法
public class Test {
public static void main(String[] args) { new Test().run(); }
int N = 20190324;
void run() {
int[] arr = new int[N + 1];
arr[1] = arr[2] = arr[3] = 1;
for (int i = 4; i <= N; i++)
arr[i] = (arr[i - 1] + arr[i - 2] + arr[i - 3]) % 10000;
System.out.printf("%04d", arr[N]);
}
}
对 10000 10000 10000 取余,保证不会溢出就行。
矩阵加速
public class Test {
public static void main(String[] args) { new Test().run(); }
int N = 20190324 - 3;
void run() {
int[][] C = {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}};
int[][] A = {{1, 1, 0}, {1, 0, 1}, {1, 0, 0}};
while (N > 0) {
if ((N & 1) == 1)
C = multi(C, A);
A = multi(A, A);
N >>= 1;
}
System.out.printf("%04d", (C[0][0] + C[1][0] + C[2][0]) % 10000);
}
int[][] multi(int[][] A, int[][] B) {
int[][] C = new int[3][3];
for (int i = 0; i < 3; ++i)
for (int j = 0; j < 3; ++j)
for (int k = 0; k < 3; ++k)
C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % 10000;
return C;
}
}
观察到数列递推式,单维且封闭,
于是考虑矩阵加速,
也没啥好说的。
#C 迷宫
本题总分: 10 10 10 分
问题描述
下图给出了一个迷宫的平面图,其中标记为 1 1 1 的为障碍,标记为 0 0 0 的为可以通行的地方。
010000
000100
001001
110000
迷宫的入口为左上角,出口为右下角,在迷宫中,只能从一个位置走到这个它的上、下、左、右四个方向之一。
对于上面的迷宫,从入口开始,可以按 D R R U R R D D D R \mathrm{DRRURRDDDR} DRRURRDDDR 的顺序通过迷宫,一共 10 10 10 步。其中 D \mathrm D D、 U \mathrm U U、 L \mathrm L L、 R \mathrm R R 分别表示向下、向上、向左、向右走。
对于下面这个更复杂的迷宫( 30 30 30 行 50 50 50 列),请找出一种通过迷宫的方式,其使用的步数最少,在步数最少的前提下,请找出字典序最小的一个作为答案。
请注意在字典序中 D < L < R < U \mathrm{D
01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR
BFS
由于答案要求在最优解中字典序最小,因此采用从终点出发,向起点做 b f s \mathrm{bfs} bfs 最短路径,
这样从起点推出来的路径必然是可达的。
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.util.ArrayDeque;
import java.util.Scanner;
import java.util.Deque;
import java.util.Queue;
public class Test {
public static void main(String[] args) { new Test().run(); }
int[][] offset = {{1, 0}, {0, -1}, {0, 1}, {-1, 0}};
char[] character = { 'D', 'L', 'R', 'U' };
int N = 30, M = 50;
void run() {
try(Scanner in = new Scanner(new FileInputStream("maze.txt"))) {
int[][] visited = new int[N + 1][M + 1];
for (int i = 1; i <= N; ++i) {
String line = in.nextLine();
for (int j = 1; j <= M; ++j)
if (line.charAt(j - 1) == '1') visited[i][j] = 0x3F3F3F3F;
}
Deque<Long> queue = new ArrayDeque();
queue.offer(makePair(N, M));
visited[N][M] = 1;
while (true) {
int x = X(queue.peek());
int y = Y(queue.peek());
if (x == 1 && y == 1) break;
queue.poll();
for (int i = 0; i < 4; ++i) {
int k = x + offset[i][0];
int g = y + offset[i][1];
if (k >= 1 && k <= N && g >= 1 && g <= M && visited[k][g] == 0) {
visited[k][g] = visited[x][y] + 1;
queue.offer(makePair(k, g));
}
}
}
int x = 1, y = 1;
while (visited[x][y] > 1)
for (int i = 0; i < 4; ++i) {
int k = x + offset[i][0];
int g = y + offset[i][1];
if (k >= 1 && k <= N && g >= 1 && g <= M && visited[k][g] == visited[x][y] - 1) {
System.out.print(character[i]);
x = k;
y = g;
break;
}
}
} catch (FileNotFoundException e) {
e.printStackTrace();
}
}
long makePair(int x, int y) { return (long)x << 32 | y; }
int X(long pair) { return (int)(pair >> 32); }
int Y(long pair) { return (int)(pair & 0xFFFFFFFF); }
}
#D 最大降雨量
本题总分: 10 10 10 分
问题描述
由于沙之国长年干旱,法师小明准备施展自己的一个神秘法术来求雨。
这个法术需要用到他手中的 49 49 49 张法术符,上面分别写着 1 1 1 至 49 49 49 这 49 49 49 个 数字。法术一共持续 7 7 7 周,每天小明都要使用一张法术符,法术符不能重复使用。
每周,小明施展法术产生的能量为这周 7 7 7 张法术符上数字的中位数。法术施展完 7 7 7 周后,求雨将获得成功,降雨量为 7 7 7 周能量的中位数。
由于干旱太久,小明希望这次求雨的降雨量尽可能大,请大最大值是多少?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
34
System.out.print(7 * 7 - 4 * 4 + 1);
七个大小为七的集合的中位数的中位数,这 7 × 7 7×7 7×7 个数中至少有 4 × 4 4 × 4 4×4 个数不小于它,如图所示:

剩下的 7 × 7 − 4 × 4 7×7-4×4 7×7−4×4 个数随便排就行了。
不是很理解这种和编程毫无关系的题,
出出来干嘛。
#E RSA 解密
本题总分: 15 15 15 分
问题描述
R S A \mathrm{RSA} RSA 是一种经典的加密算法。它的基本加密过程如下。
首先生成两个质数 p , q p, q p,q,令 n = p ⋅ q n = p\cdot q n=p⋅q,设 d d d 与 ( p − 1 ) ⋅ ( q − 1 ) (p − 1) \cdot (q − 1) (p−1)⋅(q−1) 互质,则可找到 e e e 使得 d ⋅ e d\cdot e d⋅e 除 ( p − 1 ) ⋅ ( q − 1 ) (p − 1)\cdot (q − 1) (p−1)⋅(q−1) 的余数为 1 1 1。
n , d , e n, d, e n,d,e组成了私钥, n , d n, d n,d 组成了公钥。
当使用公钥加密一个整数 X X X 时(小于 n n n),计算 C = X d m o d n C = X^d\mod\ n C=Xdmod n,则 C C C 是加密后的密文。
当收到密文 C C C 时,可使用私钥解开,计算公式为 X = C e m o d n X = C^e\ mod\ n X=Ce mod n。
例如,当 p = 5 , q = 11 , d = 3 p = 5, q = 11, d = 3 p=5,q=11,d=3 时, n = 55 , e = 27 n = 55, e = 27 n=55,e=27。
若加密数字 24 24 24,得 2 4 3 m o d 55 = 19 24^3\ mod\ 55 = 19 243 mod 55=19。
解密数字 19 19 19,得 1 9 27 m o d 55 = 24 19^{27}\ mod\ 55 = 24 1927 mod 55=24。
现在你知道公钥中 n = 1001733993063167141 , d = 212353 n = 1001733993063167141, d = 212353 n=1001733993063167141,d=212353,同时你截获了别人发送的密文 C = 20190324 C = 20190324 C=20190324,请问,原文是多少?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
Pollard’s Rho
稍微对 R S A \mathrm{RSA} RSA 有过一点了解的人,都知道,它的破解难度可以说与大数分解等价,但是否真的等同于大数分解也未有人证明,
所以这里不推荐任何读者去尝试使用分解 n n n 以外的方法去解决改题。
考虑朴素的除试法,但 O ( n ) O(\sqrt n) O(n) 的复杂度显然不是为我们所能接受的,但实际上 10s 就分解完了 。
于是考虑用 Pollard‘s Rho 分解 n n n,得到 p p p、 q q q。
观察到蓝桥出题人铁文盲,除和除以分不清楚,有 d ⋅ e ≡ 1 ( m o d ( p − 1 ) ( q − 1 ) ) d\cdot e \equiv 1 \pmod{(p-1)(q-1)} d⋅e≡1(mod(p−1)(q−1)),即 e e e 是 d d d 模 ( p − 1 ) ( q − 1 ) (p-1)(q-1) (p−1)(q−1) 下的乘法逆元。
e x g c d \mathrm{exgcd} exgcd 求出逆元后直接快速幂就行。
public class Test {
public static void main(String[] args) { new Test().run(); }
long n = 1001733993063167141L, d = 212353, C = 20190324, x, y;
void run() {
long p = n, q, r, ed;
while (p >= n)
p = pollardRho(n, (long)(Math.random() * (n - 1)) + 1);
q = n / p;
ed = (p - 1) * (q - 1);
r = exgcd(d, ed);
System.out.println(qpow(C, x + ed, n));
}
long exgcd(long a, long b) {
if (b == 0) {
x = 1; y = 0;
return a;
}
long d = exgcd(b, a % b);
long z = x;
x = y;
y = z - a / b * y;
return d;
}
long multi(long a, long b, long p) {
long res = 0;
while (b > 0) {
if (b % 2 == 1) res = (res + a) % p;
a = (a + a) % p;
b /= 2;
}
return res;
}
long qpow(long a, long b, long p) {
long res = 1;
while (b > 0) {
if (b % 2 == 1) res = multi(res, a, p);
a = multi(a, a, p);
b /= 2;
}
return res;
}
long f(long x, long c, long p) { return (multi(x, x, p) + c) % p; }
long gcd(long a, long b) { return b == 0 ? a : gcd(b, a % b); }
long pollardRho(long N, long c) {
long xi = (long)(Math.random() * (N - 1)) + 1;
long xj = f(xi, c, N);
while (xi != xj) {
long d = gcd(xi - xj, N);
if (d > 1) return d;
xj = f(f(xj, c, N), c, N);
xi = f(xi, c, N);
}
return N;
}
}
#F 完全二叉树的权值
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 15 15 15 分
问题描述
给定一棵包含 N N N 个节点的完全二叉树,树上每个节点都有一个权值,按从上到下、从左到右的顺序依次是 A 1 , A 2 , ⋅ ⋅ ⋅ A N A_1, A_2, ··· A_N A1,A2,⋅⋅⋅AN,如下图所示:
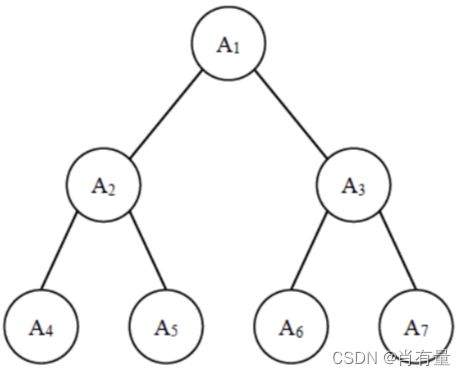
现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的节点权值之和最大?如果有多个深度的权值和同为最大,请你输出其中最小的深度。
注:根的深度是 1 1 1。
输入格式
第一行包含一个整数 N N N。
第二行包含 N N N 个整数 A 1 , A 2 , ⋅ ⋅ ⋅ A N A_1, A_2, ··· A_N A1,A2,⋅⋅⋅AN。
输出格式
输出一个整数代表答案。
测试样例1
Input:
7
1 6 5 4 3 2 1
Output:
2
评测用例规模与约定
对于所有评测用例, 1 ≤ N ≤ 100000 , − 100000 ≤ A i ≤ 100000 1≤N≤100000, -100000 ≤A_i ≤100000 1≤N≤100000,−100000≤Ai≤100000。
从完全二叉树的定义中,可以衍生出性质,对于一个深度为 d d d 的完全二叉树,它深度为 i i i, i < d i < d i<d 的节点有 2 i 2^i 2i 个,这里,根节点的深度为 0 0 0。
于是依次取出序列的前 2 i 2^i 2i 个权值,其和为深度为 i + 1 i + 1 i+1 的节点的权值和,并将其与现有的答案做比较,若序列中的元素不足 2 i 2^i 2i 个,则取到不能取为止。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.io.IOException;
public class Main {
public static void main(String[] args) { new Main().run(); }
void run() {
int n = nextInt();
long sum, ans = 1, max = -100000;
for (int len = 1, depth = 1; n > 0; len <<= 1, ++depth) {
sum = 0;
for (int i = 0; i < len && n > 0; ++i, --n) sum += nextInt();
if (sum > max) {
ans = depth;
max = sum;
}
}
System.out.println(ans);
}
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
#G 外卖店优先级
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 20 20 20 分
问题描述
“ “\: “饱了么 ” ” ” 外卖系统中维护着 N N N 家外卖店,编号 1 ∼ N 1 \sim N 1∼N。每家外卖店都有 一个优先级,初始时 ( 0 0 0 时刻) 优先级都为 0 0 0。
每经过 1 1 1 个时间单位,如果外卖店没有订单,则优先级会减少 1 1 1,最低减到 0 0 0;而如果外卖店有订单,则优先级不减反加,每有一单优先级加 2 2 2。
如果某家外卖店某时刻优先级大于 5 5 5,则会被系统加入优先缓存中;如果优先级小于等于 3 3 3,则会被清除出优先缓存。
给定 T T T 时刻以内的 M M M 条订单信息,请你计算 T T T 时刻时有多少外卖店在优先缓存中。
输入格式
第一行包含 3 个整数 N 、 M N、M N、M 和 T T T。
以下 M M M 行每行包含两个整数 t s ts ts 和 i d id id,表示 t s ts ts 时刻编号 i d id id 的外卖店收到 一个订单。
输出格式
输出一个整数代表答案。
测试样例1
Input:
2 6 6
1 1
5 2
3 1
6 2
2 1
6 2
Output:
1
Explanation:
6 时刻时, 1 号店优先级降到 3,被移除出优先缓存; 2 号店优先级升到 6,
加入优先缓存。所以是有 1 家店 (2 号) 在优先缓存中。
评测用例规模与约定
对于 80 80 80% 的评测用例, 1 ≤ N , M , T ≤ 10000 1 ≤ N, M, T ≤ 10000 1≤N,M,T≤10000。
对于所有评测用例, 1 ≤ N , M , T ≤ 100000 , 1 ≤ t s ≤ T , 1 ≤ i d ≤ N 1 ≤ N, M, T ≤ 100000,1 ≤ ts ≤ T,1 ≤ id ≤ N 1≤N,M,T≤100000,1≤ts≤T,1≤id≤N。
中规中矩的模拟题,没啥好说的。
算了,
不是长篇阅读理解的,
都是好题。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.io.IOException;
import java.util.Arrays;
public class Main {
public static void main(String[] args) { new Main().run(); }
void run() {
int ans = 0, n = nextInt(), m = nextInt(), t = nextInt();
int[] level = new int[n + 1], last = new int[n + 1];
boolean[] first = new boolean[n + 1];
Order[] orders = new Order[m];
for (int i = 0; i < m; ++i)
orders[i] = new Order(nextInt(), nextInt());
Arrays.sort(orders);
for (int i = 0; i < m; ++i) {
int ts = orders[i].ts;
int id = orders[i].id;
if (ts > last[id])
level[id] = max(0, level[id] - ts + last[id] + 1);
if (level[id] <= 3) first[id] = false;
level[id] += 2;
if (level[id] > 5) first[id] = true;
last[id] = ts;
}
for (int i = 1; i <= n; ++i) {
if (level[i] - t + last[i] <= 3) first[i] = false;
if (first[i]) ++ans;
}
System.out.println(ans);
}
int max(int a, int b) { return a > b ? a : b; }
class Order implements Comparable<Order> {
int ts, id;
Order(int ts, int id) {
this.ts = ts;
this.id = id;
}
public int compareTo(Order order) { return this.ts - order.ts; }
}
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
#H 修改数组
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 20 20 20 分
问题描述
给定一个长度为 N N N 的数组 A = [ A 1 , A 2 , ⋅ ⋅ ⋅ , A N ] A = [A_1,A_2,··· ,A_N] A=[A1,A2,⋅⋅⋅,AN],数组中有可能有重复出现的整数。
现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改 A 2 , A 3 , ⋅ ⋅ ⋅ , A N A_2,A_3,··· ,A_N A2,A3,⋅⋅⋅,AN。
当修改 A i A_i Ai 时,小明会检查 A i A_i Ai 是否在 A 1 ∼ A i − 1 A_1 \sim A_{i-1} A1∼Ai−1 中出现过。如果出现过,则小明会给 A i A_i Ai 加上 1 1 1;如果新的 A i A_i Ai 仍在之前出现过,小明会持续给 A i A_i Ai 加 1 1 1 ,直到 A i A_i Ai 没有在 A 1 ∼ A i − 1 A_1 \sim A_{i-1} A1∼Ai−1 中出现过。
当 A N A_N AN 也经过上述修改之后,显然 A A A 数组中就没有重复的整数了。
现在给定初始的 A A A 数组,请你计算出最终的 A A A 数组。
输入格式
第一行包含一个整数 N N N。
第二行包含 N N N 个整数 A 1 , A 2 , ⋅ ⋅ ⋅ , A N A_1,A_2,··· ,A_N A1,A2,⋅⋅⋅,AN。
输出格式
输出 N N N 个整数,依次是最终的 A 1 , A 2 , ⋅ ⋅ ⋅ , A N A_1,A_2,··· ,A_N A1,A2,⋅⋅⋅,AN。
测试样例1
Input:
5
2 1 1 3 4
Output:
2 1 3 4 5
评测用例规模与约定
对于 80 80 80% 的评测用例, 1 ≤ N ≤ 10000 1 ≤ N ≤ 10000 1≤N≤10000。
对于所有评测用例, 1 ≤ N ≤ 100000 , 1 ≤ A i ≤ 1000000 1 ≤ N ≤ 100000,1 ≤ A_i ≤ 1000000 1≤N≤100000,1≤Ai≤1000000。
并查集
如果我们将一个集合中的最大元素选出来作为集合的代表,
容易想到这道题关于并查集的解法,具体地说:
按 A i A_i Ai 每个可能的取值划分集合,一开始有 2 2 2 倍 max { A i } \max\{A_i\} max{Ai} 个孤立的单元集,当我们需要其中某个值时,查询这个值所在的集合的最大元素,即集合的标识,使用它然后将该集合与标识 + 1 +1 +1 合并。
请读者思考为什么这么做是正确的。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.io.IOException;
import java.io.PrintWriter;
public class Main {
public static void main(String[] args) { new Main().run(); }
int[] linked = new int[2000010];
void run() {
for (int i = 1; i < linked.length; ++i) linked[i] = i;
PrintWriter out = new PrintWriter(System.out);
int n = nextInt();
for (int i = 0; i < n; ++i) {
out.print(find(nextInt()));
out.write(' ');
}
out.flush();
}
int find(int x) {
if (x == linked[x]) {
linked[x] = x + 1;
return x;
}
return linked[x] = find(linked[x]);
}
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
但其实在针对上面程序,很容易捏出 H a c k \mathrm{Hack} Hack 数据。
当输入的数据为:
n n n
1 2 3 ⋯ n − 1 1 1\ 2\ 3\ \cdots \ n-1\ 1 1 2 3 ⋯ n−1 1
在最后一次 f i n d \mathrm{find} find 中,需要的方法栈大小达到了 O ( n ) O(n) O(n) 级,这会直接导致我们的程序抛出 StackOverflowError 异常。
考虑平衡二叉树的解法,具体地说:
我们将 A i A_i Ai 每个可能的取值插入到数中,然后依次考虑每个 A i A_i Ai,若 A i A_i Ai 在树中,则取出它,否则取出 A i A_i Ai 的后继节点。
但 J D K \mathrm{JDK} JDK 实现的 T r e e S e t \mathrm{TreeSet} TreeSet 常数太大,经实际测试无法通过全部的用例,自己去实现一个代码量又太大,所以下面介绍一种平衡树的下级替代。
树状数组上倍增
如果定义一个序列 S = { s i ∣ 1 o r 0 } S = \{s_i| 1\ or\ 0\} S={si∣1 or 0},当 s i = 1 s_i = 1 si=1 时代表 i i i 这个数被取过, 0 0 0 则恰反。
当存在一对 i i i、 j j j 使得 ∑ i j s i = j − i + 1 \sum_i^js_i = j - i + 1 ∑ijsi=j−i+1 成立,就表示 [ i , j ] [i,j] [i,j] 之间所有的数都被取出来过,因此在 A i A_i Ai 确定后我们将 s A i s_{A_i} sAi 置为 1 1 1,而当我们发现 A i A_i Ai 被取过后从 A i A_i Ai 开始倍增的寻找一段最长的连续被取区间,右端点 + 1 +1 +1 即是我们最后要确定的 A i A_i Ai。
这样做的复杂度在 O ( n log 2 A ) O(n\log^2A) O(nlog2A),但因为树状数组和倍增搜索的常数都极小,因此能通过所有的测试用例,而且性能表现几乎与并查集相同。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.io.IOException;
import java.io.PrintWriter;
public class Main {
public static void main(String[] args) { new Main().run(); }
int N = 2000010;
int[] tree = new int[N + 1];
boolean[] marked = new boolean[N + 1];
void run() {
PrintWriter out = new PrintWriter(System.out);
int n = nextInt();
for (int i = 1; i <= n; ++i) {
int a = nextInt();
if (marked[a]) {
int b = a;
int left = sum(a);
for (int offset = 1 << 20; offset > 0; offset >>= 1)
if (b + offset <= N && sum(b + offset) - left == b + offset - a) b += offset;
a = b + 1;
}
out.print(a);
out.write(' ');
marked[a] = true;
add(a);
}
out.flush();
}
void add(int i) { while (i <= N) { ++tree[i]; i += lowBit(i); } }
int sum(int i) {
int res = 0;
while (i > 0) {
res += tree[i];
i -= lowBit(i);
}
return res;
}
int lowBit(int k) { return k & -k; }
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
#I 糖果
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 25 25 25 分
问题描述
糖果店的老板一共有 M M M 种口味的糖果出售。为了方便描述,我们将 M M M 种口味编号 1 ∼ M 1 \sim M 1∼M。
小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果,而是 K K K 颗一包整包出售。
幸好糖果包装上注明了其中 K K K 颗糖果的口味,所以小明可以在买之前就知道每包内的糖果口味。
给定 N N N 包糖果,请你计算小明最少买几包,就可以品尝到所有口味的糖果。
输入格式
第一行包含三个整数 N , M , K N,M,K N,M,K。
接下来 N N N 行每行 K K K 个整数 T 1 , T 2 , ⋅ ⋅ ⋅ , T K T_1,T_2,··· ,T_K T1,T2,⋅⋅⋅,TK,代表一包糖果的口味。
输出格式
输出一个整数表示答案。如果小明无法品尝所有口味,输出 − 1 −1 −1。
测试样例1
Input:
6 5 3
1 1 2
1 2 3
1 1 3
2 3 5
5 4 2
5 1 2
Output:
2
评测用例规模与约定
对于 30 30 30% 的评测用例, 1 ≤ N ≤ 20 1 ≤ N ≤ 20 1≤N≤20。
对于所有评测用例, 1 ≤ N ≤ 100 , 1 ≤ M ≤ 20 , 1 ≤ K ≤ 20 , 1 ≤ T i ≤ M 1 ≤ N ≤ 100,1 ≤ M ≤ 20,1 ≤ K ≤ 20,1 ≤ T_i ≤ M 1≤N≤100,1≤M≤20,1≤K≤20,1≤Ti≤M。
状压 DP
模板题,
没什么好说的。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.io.IOException;
import java.util.Arrays;
public class Main {
public static void main(String[] args) { new Main().run(); }
void run() {
int n = nextInt(), m = nextInt(), k = nextInt();
int[] dp = new int[1 << m];
Arrays.fill(dp, 0x3F3F3F3F);
dp[0] = 0;
for (int i = 1; i <= n; ++i) {
int candy = 0;
for (int j = 0; j < k; ++j)
candy |= 1 << nextInt() - 1;
for (int j = 0; j < 1 << m; ++j)
dp[j | candy] = min(dp[j | candy], dp[j] + 1);
}
if (dp[(1 << m) - 1] != 0x3F3F3F3F)
System.out.println(dp[(1 << m) - 1]);
else System.out.println("-1");
}
int min(int a, int b) { return a < b ? a : b; }
int min(int a, int b, int c) { return min(a, min(b, c)); }
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
#J 组合数问题
时间限制: 5.0 s 5.0\mathrm s 5.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 25 25 25 分
问题描述
给 n , m , k n,m,k n,m,k 求有多少对 ( i , j ) (i, j) (i,j) 满足 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n, 0 ≤ j ≤ min ( i , m ) 0 \leq j \leq \min(i,m) 0≤j≤min(i,m) 且 C i j ≡ 0 ( m o d k ) C_i^j \equiv 0\pmod k Cij≡0(modk), k k k 是质数。其中 C i j C_i^j Cij 是组合数,表示从 i i i 个不同的数中选出 j j j 个组成 一个集合的方案数。
输入格式
第一行两个数 t , k t,k t,k,其中 t t t 代表该测试点包含 t t t 组询问, k k k 的意思与上文中相同。
接下来 t t t 行每行两个整数 n , m n,m n,m,表示一组询问。
输出格式
输出 t t t 行,每行一个整数表示对应的答案。由于答案可能很大,请输出答案除以 1 0 9 + 7 10^9 + 7 109+7 的余数。
测试样例1
Input:
1 2
3 3
Output:
1
Explanation:
在所有可能的情况中,只有 C_2^1=2 是 2 的倍数。
测试样例2
Input:
2 5
4 5
6 7
Output:
0
7
测试样例3
Input:
3 23
23333333 23333333
233333333 233333333
2333333333 2333333333
Output:
851883128
959557926
680723120
评测用例规模与约定
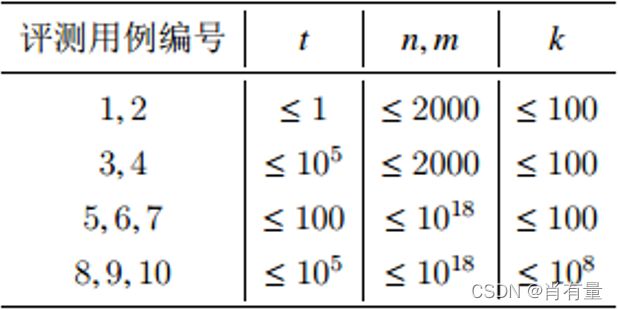
对于所有评测用例, 1 ≤ k ≤ 1 0 8 , 1 ≤ t ≤ 1 0 5 , 1 ≤ n , m ≤ 1 0 18 1 \leq k \leq 10^8,1 \leq t \leq 10^5,1 \leq n,m \leq 10^{18} 1≤k≤108,1≤t≤105,1≤n,m≤1018,且 k k k 是质数。
评测时将使用 10 10 10 个评测用例测试你的程序,每个评测用例的限制如下:
Lucas 定理
卢卡斯定理常用于求解大组合数取模问题,因此在许多人眼里他长这样: C n m ≡ C n / p m / p ⋅ C n m o d p m m o d p ( m o d p ) C_n^m \equiv C_{n/p}^{m/p} \cdot C_{n\ \ \:\mathrm{mod}\ p}^{m\;\mathrm{mod}\ p} \pmod p Cnm≡Cn/pm/p⋅Cn mod pmmod p(modp) 但实际上人家长这样: n = n k p k + n k − 1 p k − 1 + ⋯ + n 1 p + n 0 m = m k p k + m k − 1 p k − 1 + ⋯ + m 1 p + m 0 C n m ≡ C n k m k ⋅ C n k − 1 m k − 1 ⋅ ⋯ ⋅ C n 1 m 1 ⋅ C n 0 m 0 ( m o d p ) \begin{aligned}&n = n_kp^k + n_{k-1}p^{k-1} + \cdots + n_1p + n_0\\&m = m_kp^k + m_{k-1}p^{k-1} + \cdots + m_1p + m_0\\&C_n^m\equiv C_{n_k}^{m_k}\cdot C_{n_{k - 1}}^{m_{k - 1}}\cdot\: \cdots\:\cdot C_{n_1}^{m_1}\cdot C_{n_0}^{m_0}\pmod p\end{aligned} n=nkpk+nk−1pk−1+⋯+n1p+n0m=mkpk+mk−1pk−1+⋯+m1p+m0Cnm≡Cnkmk⋅Cnk−1mk−1⋅⋯⋅Cn1m1⋅Cn0m0(modp) 在我眼里这就可列数列求和使用求和符号一样耳目一新吧。
简单证明一下就是,
由 p p p 为质数可得知,若 1 ≤ i < p 1 \leq i < p 1≤i<p,则 C p i ≡ 0 ( m o d p ) C_p^i \equiv 0 \pmod p Cpi≡0(modp),所以
( 1 + x ) p = 1 + C p 1 x + C p 2 x 2 + ⋯ + C p p − 1 x p − 1 + x p ≡ 1 + x p ( m o d p ) \begin{aligned}(1+x)^p &= 1 + C_p^1x + C_p^2x^2 + \cdots + C_p^{p-1}x^{p-1} + x^p\\ &\equiv 1 + x^p &\pmod p\end{aligned} (1+x)p=1+Cp1x+Cp2x2+⋯+Cpp−1xp−1+xp≡1+xp(modp)
设 f ( x ) = 1 + x f(x) = 1 + x f(x)=1+x,则 C n m = [ x m ] f n ( x ) C_n^m = [x^m]f^n(x) Cnm=[xm]fn(x),
f n ( x ) = ( 1 + x ) n 0 ( ( 1 + x ) p ) n 1 ⋯ ( ( 1 + x ) p k ) n k ≡ ( 1 + x ) n 0 ( 1 + x p ) n 1 ⋯ ( 1 + x p k ) n k ( m o d p ) \begin{aligned}f^n(x) &= (1+x)^{n_0}((1+x)^p)^{n_1} \cdots((1+x)^{p^k})^{n_k}\\&\equiv (1+x)^{n_0}(1+x^p)^{n_1} \cdots(1+x^{p^k})^{n_k}&\pmod p\end{aligned} fn(x)=(1+x)n0((1+x)p)n1⋯((1+x)pk)nk≡(1+x)n0(1+xp)n1⋯(1+xpk)nk(modp)
因为 m m m 的 p p p 进制拆分法唯一,所以
[ x m ] f n ( x ) ≡ [ x m 0 ] f n 0 ( x ) ⋅ [ x m 1 ] f n 1 ( x ) ⋅ ⋯ ⋅ [ x m k ] f n k ( x ) ( m o d p ) [x^m]f^n(x) \equiv [x^{m_0}]f^{n_0}(x)\cdot[x^{m_1}]f^{n_1}(x)\cdot\ \cdots\ \cdot [x^{m_k}]f^{n_k}(x)\pmod p [xm]fn(x)≡[xm0]fn0(x)⋅[xm1]fn1(x)⋅ ⋯ ⋅[xmk]fnk(x)(modp)
故 C n m ≡ C n k m k ⋅ C n k − 1 m k − 1 ⋅ ⋯ ⋅ C n 1 m 1 ⋅ C n 0 m 0 ( m o d p ) C_n^m\equiv C_{n_k}^{m_k}\cdot C_{n_{k - 1}}^{m_{k - 1}}\cdot\: \cdots\:\cdot C_{n_1}^{m_1}\cdot C_{n_0}^{m_0}\pmod p Cnm≡Cnkmk⋅Cnk−1mk−1⋅⋯⋅Cn1m1⋅Cn0m0(modp) 成立。
当 m < 0 m < 0 m<0 或 m > n m > n m>n 时 C n m = 0 C_n^m = 0 Cnm=0,
原命题从而转为存在多少对 i i i、 j j j, 1 ≤ i ≤ n , 0 ≤ j ≤ min ( i , m ) 1≤i≤n,0≤j≤\min(i,m) 1≤i≤n,0≤j≤min(i,m),在 p p p 进制下一个数位 k k k,使得 [ i k ] p < [ j k ] p [i_k]_p < [j_k]_p [ik]p<[jk]p 成立,这里我们统计它的对立事件,即满足前面的所有条件下,有多对 i i i、 j j j 在 p p p 进制下, i i i 的每一位都大于 j j j,最后用全体事件减去它,就得到了我们想要的答案。
于是考虑数位 d p \mathrm{dp} dp,这里将 i i i、 j j j 变化符号为 x x x、 y y y 以增强推导过程的可读性,对于 x x x、 y y y 的第 i i i 位可行的取值与第 i i i 位之前所有的取值是否到达上界有关,于是划分出 4 4 4 个状态 f i , k f_{i,k} fi,k, k = 0 , 1 , 2 , 3 k = 0,1,2,3 k=0,1,2,3,分别表示 x / p i x / p^i x/pi 和 y / p i y / p^i y/pi 的取值均为达到上界; x / p i x / p^i x/pi 达到上界; y / p i y/p^i y/pi 达到上界;两者均达到上界;时, x / p i x / p^i x/pi 的任意一位都大于 y / p i y / p^i y/pi 的组合数。
显然当 ∑ i = 0 3 f 0 , i \sum_{i=0}^3f_{0,i} ∑i=03f0,i 等于 x x x 的任意一位都大于 y y y 的组合数, ( m + 1 ) ( n − m ) + m ( m + 3 ) 2 − ∑ i = 0 3 f 0 , i (m + 1)(n - m) + \cfrac{m(m + 3)}2 - \sum_{i=0}^3f_{0,i} (m+1)(n−m)+2m(m+3)−∑i=03f0,i 为答案( m > n m > n m>n 时将 m m m 置为 n n n)。
设函数 c a l c ( x , y ) calc(x,y) calc(x,y) 为取值不超过 x x x 的 x ′ x' x′ 和不超过 y y y 的 y ′ y' y′ 组合个数。
c a l c x ( x , y ) calc_x(x,y) calcx(x,y) 为取值不超过 y y y 且小于 x x x 的 y ′ y' y′ 个数。
c a l c y ( x , y ) calc_y(x,y) calcy(x,y) 为取值不超过 x x x 且大于 y y y 的 x ′ x' x′ 个数。
现在考虑转移,设 x i x_i xi 为 x x x 在第 i + 1 i + 1 i+1 位上的数, y i y_i yi 同理。
f i , 0 = f i + 1 , 0 × c a l c ( k − 1 , k − 1 ) + f i + 1 , 1 × c a l c ( x i − 1 , k − 1 ) + f i + 1 , 2 × c a l c ( k − 1 , y i − 1 ) + f i + 1 , 3 × c a l c ( x i − 1 , y i − 1 ) f_{i,0} = f_{i+1,0} × calc(k-1,k-1) + f_{i+1,1} × calc(x_i-1,k-1) + f_{i+1,2} × calc(k-1,y_i-1) + f_{i+1,3} × calc(x_i-1,y_i-1) fi,0=fi+1,0×calc(k−1,k−1)+fi+1,1×calc(xi−1,k−1)+fi+1,2×calc(k−1,yi−1)+fi+1,3×calc(xi−1,yi−1)
f i , 1 = f i + 1 , 1 × c a l c x ( x i , k − 1 ) + f i + 1 , 3 × c a l c x ( x i , y i − 1 ) f_{i,1}=f_{i+1,1} × calc_x(x_i, k-1) + f_{i+1,3} × calc_x(x_i, y_i-1) fi,1=fi+1,1×calcx(xi,k−1)+fi+1,3×calcx(xi,yi−1)
f i , 2 = f i + 1 , 2 × c a l c y ( k − 1 , y i ) + f i + 1 , 3 × c a l c y ( x i − 1 , y i ) f_{i,2}=f_{i+1,2} × calc_y(k-1, y_i) + f_{i+1,3} × calc_y(x_i-1, y_i) fi,2=fi+1,2×calcy(k−1,yi)+fi+1,3×calcy(xi−1,yi)
f i , 3 = f i + 1 , 3 ∣ x i ≥ y i f_{i,3}=f_{i+1,3}\ |\ x_i \geq y_i fi,3=fi+1,3 ∣ xi≥yi
初始时, f ⌈ log k ( n + 1 ) ⌉ , 3 = 1 f_{\lceil\log_k(n+1)\rceil,3} = 1 f⌈logk(n+1)⌉,3=1,其余为 0 0 0。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import java.io.PrintWriter;
import java.io.IOException;
public class Main {
public static void main(String[] args) { new Main().run(); }
int p = 1000000007, inv2 = 500000004;
void run() {
PrintWriter out = new PrintWriter(System.out);
long[] kpow = new long[64];
int t = nextInt(), k = nextInt(), N = 0;
kpow[0] = 1;
for (int i = 1; ; ++i)
if (kpow[i - 1] == kpow[i - 1] * k / k)
kpow[i] = kpow[i - 1] * k;
else {
N = i;
break;
}
long[][] dp = new long[N + 1][4];
dp[N][3] = 1;
while (t-- > 0) {
long n = nextLong(), m = nextLong();
if (m > n) m = n;
for (int i = N - 1; i >= 0; --i) {
long ni = n / kpow[i] % k;
long mi = m / kpow[i] % k;
dp[i][0] = (dp[i + 1][0] * calc(k - 1, k - 1) + dp[i + 1][1] * calc(ni - 1, k - 1) + dp[i + 1][2] * calc(k - 1, mi - 1) + dp[i + 1][3] * calc(ni - 1, mi - 1)) % p;
dp[i][1] = (dp[i + 1][1] * calcn(ni, k - 1) + dp[i + 1][3] * calcn(ni, mi - 1)) % p;
dp[i][2] = (dp[i + 1][2] * calcm(k - 1, mi) + dp[i + 1][3] * calcm(ni - 1, mi)) % p;
dp[i][3] = ni >= mi ? dp[i + 1][3] : 0;
}
out.println(((calc(n, m) - dp[0][0] - dp[0][1] - dp[0][2] - dp[0][3]) % p + p) % p);
}
out.flush();
}
long calc(long n, long m) {
if (n <= m) {
n %= p;
return (n + 1) * (n + 2) % p * inv2 % p;
}
n %= p;
m %= p;
return ((m + 1) * (n - m) % p + (m + 1) * (m + 2) % p * inv2 % p) % p;
}
long calcn(long n, long m) { return n > m ? m + 1 : n + 1; }
long calcm(long n, long m) { return n < m ? 0 : n - m + 1; }
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer token;
String next() {
if (token == null || !token.hasMoreTokens())
try {
token = new StringTokenizer(reader.readLine());
} catch (IOException e) {
e.printStackTrace();
}
return token.nextToken();
}
int nextInt() { return Integer.parseInt(next()); }
long nextLong() { return Long.parseLong(next()); }
}