第十章 深度强化学习-Prioritized Replay DQN
![]()
获取更多资讯,赶快关注上面的公众号吧!
文章目录
- 第十章 深度强化学习-Prioritized Replay DQN
-
- 10.1 介绍-说明经验回放随机采样存在的问题
- 10.2 优先级回放
-
- 10.2.1 一个启发性的例子
- 10.2.2 基于TD误差的优先级排序
- 10.2.3 随机优先级
- 10.2.4 降低偏差
- 10.3 ATARI实验结果
- 参考文献
第十章 深度强化学习-Prioritized Replay DQN

论文地址:https://arxiv.org/pdf/1511.05952.pdf
本文是Google DeepMind于2016年2月提出的一篇通过引入优先级经验回放提高深度强化学习性能的文章,发表在顶级会议ICLR2016上,作者Tom Schaul在经验回放的基础上考虑了这些经验的重要性差异,并将优先级经验回放用于Deep Q-Networks(DQN),得到了更佳的实验结果。
正常论文的阅读方式,先看摘要和结论:

经验回放使得在线强化学习可以存储并重用历史经验,在之前的工作中,经验转移是从经验池中均匀随机采样的,这样做的弊端在于仅仅按照以原始经历的相同的频率回放转移,而与重要性无关。在本文中,作者建立了一个优先级经验框架,以便更频繁地回放重要的转移,从而更有效地进行学习。作者还将优先级经验回放用于DQN,实现表明基于优先级回放的DQN在49个游戏中有41个优于基于均匀回放的DQN。

本文提出了一种优先级回放方法,可以使得从经验回放中更有效地学习,研究了几个变体,设计了适用于大规模回放经验池的实现,并发现优先级回放可以将学习速度提高2倍,并在雅达利基准上达到了一个新的最优性能。我们列出了更多的针对类不平衡监督学习的变体和扩展。
10.1 介绍-说明经验回放随机采样存在的问题
在线强化学习代理在观察一连串的经验时是增量式地更新参数的, 最简单的形式就是每次更新后就立即丢掉输入数据,但这会造成两个问题:
- 这种强相关的更新打破了许多常用的基于随机梯度下降算法的独立同分布条件,造成算法学习不稳定甚至不收敛;
- 很可能会迅速遗弃一些在将来会很有用的稀缺经验。
1992年Lin提出的经验回放(Experience replay) 可以解决上面的两个问题,通过将经验进行回放存储,就有可能通过混合或多或少最近用于更新的经验来打破时间上的关联,并且稀缺经验可以用于不止一次更新。
在Prioritized Replay DQN之前,我们已经讨论了很多种DQN,比如Nature DQN, DDQN等,他们都是通过经验回放来采样,进而做目标Q值的计算的。在采样的时候,我们是一视同仁,在经验回放池里面的所有样本都有相同的被采样到的概率。
但是注意到在经验回放池里面的不同样本由于TD误差的不同,对我们反向传播的作用是不一样的。TD误差越大,那么对我们反向传播的作用越大。而TD误差小的样本,由于TD误差小,对反向梯度的计算影响不大。在Q网络中,TD误差就是目标Q网络计算的目标Q值和当前Q网络计算的Q值之间的差距。
这样如果TD误差的绝对值|δ(t)|较大的样本更容易被采样,则我们的算法会比较容易收敛。下面我们看看Prioritized Replay DQN的算法思路。
10.2 优先级回放
在利用经验池的时候会面临两个层面的设计选择:
- 存储哪些经验;
- 如何进行回放。
文中仅针对第二项-如何最有效地利用回放记忆进行学习。首先通过一个深有启发的例子开始说明如何逐步地加入经验回放算法。
10.2.1 一个启发性的例子
为了更好地理解优先级的潜在好处,作者引入了一个人工的“Blind Cliffwalk”环境来例证当奖励稀疏时探索的挑战性,如图1所示。在只有n个状态的情况下,环境就需要指数随机步才能获得第一个非零的奖励,准确地说,一个随机动作序列得到奖励的概率是2-n,而且大多数相关的转移(来自为数不多的成功)会隐匿于茫茫的失败信息中。

作者就是使用这个例子来突出两个代理在学习次数上的差异,两个代理均对从相同回放记忆中抽取的变迁执行Q学习更新,不同的是第一个代理随机均匀回放,第二代理则是调用oracle对转移进行优先级排序,oracle贪婪地选择能够最大限度降低当前状态下全局误差的转移。详细过程如下:
使用Q学习的直接形式(详细),Q值可以通过查找表,也可以通过线性函数逼近器表示为 Q ( s , a ) : = θ ⊤ ϕ ( s , a ) Q(s, a):=\theta^{\top} \phi(s, a) Q(s,a):=θ⊤ϕ(s,a)。对于每一个转移,使用下式计算TD误差:
δ t : = R t + γ t max a Q ( S t , a ) − Q ( S t − 1 , A t − 1 ) \delta_{t}:=R_{t}+\gamma_{t} \max _{a} Q\left(S_{t}, a\right)-Q\left(S_{t-1}, A_{t-1}\right) δt:=Rt+γtamaxQ(St,a)−Q(St−1,At−1)
并采用随机梯度下降进行参数更新:
θ ← θ + η ⋅ δ t ⋅ ∇ θ Q ∣ S t − 1 , A t − 1 = θ + η ⋅ δ t ⋅ ϕ ( S t − 1 , A t − 1 ) \theta \leftarrow \theta+\left.\eta \cdot \delta_{t} \cdot \nabla_{\theta} Q\right|_{S_{t-1}, A_{t-1}}=\theta+\eta \cdot \delta_{t} \cdot \phi\left(S_{t-1}, A_{t-1}\right) θ←θ+η⋅δt⋅∇θQ∣St−1,At−1=θ+η⋅δt⋅ϕ(St−1,At−1)
最后的实验结果(如图2)表明以较好的顺序选择转移可以达到指数级的加速,这就激励作者寻找一种实际的方法来提升均匀随机回放。

10.2.2 基于TD误差的优先级排序
度量转移重要性的准则是优先级回放的核心,一种理想的准则是RL代理可以从当前状态下的转移中学习的多少,但这并不能直接得到。一种合理的方法是使用转移的TD误差 δ \delta δ,这个值表示当前Q值与目标Q值有多大的差距。这个方法特别适应于增量式的在线RL算法,如SARSA或Q学习,因为算法已经计算出了TD误差并且按 δ \delta δ的比例进行参数更新。但是当奖励有noisy的时候,TD误差估计优先级也会很糟糕。
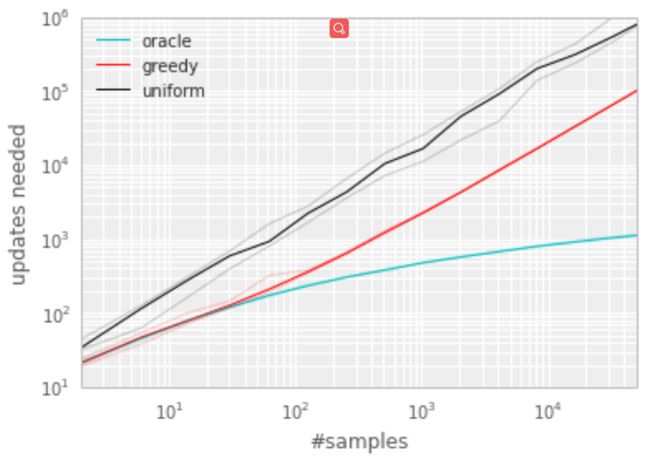
为了说明基于TD误差的优先级回放的潜在有效性,在’Blind Cliffwalk’环境下将均匀和oracle基准与贪婪TD误差的优先级算法进行了比较。该算法在经验池中存储了每个转移最后得到的TD误差,用这种方式,带有最大绝对TD错误的转移将用于回放。这里的转移采用Q学习进行更新,其按TD误差的比例更新权重。如果当一个新的转移到来时并不知道它的TD误差,那么就把这个转移的TD误差值设置为最大,这样可以保证所有的经验都会被至少回放一次。图3显示了该算法大大减少了解决“Blind Cliffwalk”任务所需的工作量。
实现:为了能够扩展到大经验池容量N,我们用二进制堆数据结构(binary heap data structure)来存储优先级序列。这样找到找到最高优先级的转移的复杂度是O(1),更新优先级的复杂度 为O(logN)。
10.2.3 随机优先级
然而贪婪TD误差优先级也存在一些问题:
- 未避免扫描整个经验池带来的昂贵代价,只会对回放的转移进行TD误差的更新,结果就是初次访问过的具有很小TD误差的转移会长时间的不会被回放;
- TD对噪声峰值(当奖励随机时)很敏感,容易将源于噪声的估计误差加入;
- 最后,贪婪优先级关注的是经验的一小部分:误差减少缓慢,特别是在使用函数逼近时,这意味着初始时高误差的转移会被频繁地回放,这种多样性的缺乏使得系统容易过拟合。
为了克服这些问题,作者提出了一种介于纯贪婪优先级和均匀随机抽样之间的随机抽样方法,确保了采样概率是按转移优先级单调的,同时又能保证即使对于最低优先级的转移也会有非零的概率。具体地,将转移i的采样概率定义为:
P ( i ) = p i α ∑ k p k α (1) P(i)=\frac{p_{i}^{\alpha}}{\sum_{k} p_{k}^{\alpha}}\tag {1} P(i)=∑kpkαpiα(1)
其中 p i > 0 p_{i}>0 pi>0为转移i的优先级。指数α决定了使用多少优先级,如果α=0那么就对应均匀随机采样。
对于优先级的定义作者提出了两种变体:
- 第一种变体是直接的比例优先级 p i = ∣ δ i ∣ + ϵ p_{i}=\left|\delta_{i}\right|+\epsilon pi=∣δi∣+ϵ,其中 ϵ \epsilon ϵ为一很小的正常数,以使一些TD误差为0 的极端转移特例也能够被抽取。
- 第二种是非直接的基于排名的优先级 p i = 1 rank ( i ) p_{i}=\frac{1}{\operatorname{rank}(i)} pi=rank(i)1,其中rank(i)为当经验池按照 ∣ δ i ∣ \left|\delta_{i}\right| ∣δi∣排序时转移i的排名。这种情况下,P将成为指数为 α \alpha α的幂律分布。
对于这两种变体,P都关于 ∣ δ ∣ \left|\delta\right| ∣δ∣是单调的,但是第二种变体由于对异常值不敏感,可能更具有鲁棒性。但是经过试验,这两种变体都可以加速算法收敛:

实现:为了有效地从分布(1)采样,复杂度不能依赖于N。
对于基于排名的变体,可以用一个分段线性函数来近似累积密度函数,k段的概率是相等的,分段边界可以预先计算出来(因为只有N或 α \alpha α变化时才变化)。在运行时,我们选择一个片段,然后在这个片段中的所有转移中均匀地采样。这种方法与基于小批量的学习算法结合使用效果特别好:选k为minibatch大小,从每一个片段中选出一个转移——这是一种分层抽样,可以平衡minibatch。
对于基于比例的变体稍稍不同,其利用了一种更有效的更新和取样实现方式:基于“sum-tree”的数据结构,其在本质上非常类似于二进制堆的数组表示,但是,父节点的值是其子节点的和,而不是通常的堆属性。叶节点存储转移优先级,内部节点是中间和,父节点包含所有优先级的和ptotal。这提供了一种计算优先级累积和的有效方法,允许更新和抽样的复杂度为O(log N)。为了采样大小为k的minibatch,将范围[0,ptotal]等分为k个范围,然后从每个范围内随机均匀采样一个值,最后,从树中检索与每个采样值对应的转移。开销类似于基于优先级的排序。
所有的经验回放样本只保存在最下面的叶子节点上面,一个节点一个样本。内部节点不保存样本数据。而叶子节点除了保存数据以外,还要保存该样本的优先级,就是图中的显示的数字。对于内部节点每个节点只保存自己的子节点的优先级值之和,如图中内部节点上显示的数字。
这样保存有什么好处呢?主要是方便采样。以上面的树结构为例,根节点是42,如果要采样一个样本,那么我们可以在[0,42]之间做均匀采样,采样到哪个区间,就是哪个样本。比如我们采样到了26, 在(25-29)这个区间,那么就是第四个叶子节点被采样到。而注意到第三个叶子节点优先级最高,是12,它的区间13-25也是最长的,会比其他节点更容易被采样到。
如果要采样个样本,我们可以在[0,21],[21,42]两个区间做均匀采样,方法和上面采样一个样本类似。
抽样时, 我们会将p的总合除以 batch size, 分成 batch size 那么多区间(n= sum ( p ) batchsize \frac{\operatorname{sum}(p)}{\text { batchsize }} batchsize sum(p)),如果将所有 node 的 优先级 加起来是42的话,如果抽6个样本, 这时的区间拥有的优先级可能是这样:
[0-7], [7-14], [14-21], [21-28], [28-35], [35-42]
然后在每个区间里随机选取一个数,比如在区间[21-28]里选到了24, 就按照这个24从最顶上的42开始向下搜索。首先看到最顶上42下面有两个 child nodes,拿着手中的24对比左边的 child29,如果左边的child 比自己手中的值大,那我们就走左边这条路,接着再对比29下面的左边那个点13,这时,手中的 24比13大,那我们就走右边的路,并且将手中的值根据13修改一下,变成24-13=11。接着拿着11和16左下角的12比,结果12比11大,那我们就选12当做这次选到的 优先级,并且也选择12对应的数据。
10.2.4 降低偏差
随机更新的期望值估计依赖于与期望相同的分布相对应的更新。优先级回放引入了偏差,因为它以不受控制的方式改变了这个分布,因此改变了估计将收敛到的解(即使策略和状态分布是固定的)。我们可以通过使用重要度抽样(IS)权重来纠正这个偏差:
w i = ( 1 N ⋅ 1 P ( i ) ) β w_{i}=\left(\frac{1}{N} \cdot \frac{1}{P(i)}\right)^{\beta} wi=(N1⋅P(i)1)β
如果β=1就完全补偿了非均匀概率P(i)。这些权重可以通过使用 w i δ i w_{i}\delta_{i} wiδi而不是 δ i \delta_{i} δi来加入到Q学习更新中。出于稳定性的原因,总是通过1/maxi wi将权值标准化,这样它们只会向下缩放更新。
在典型的强化学习场景中,更新的无偏性在训练结束接近收敛时是最重要的,由于策略、状态分布和自举目标的变化,该过程无论如何都是非平稳的。因此随着时间的推移,对重要性采样校正量进行退火处理,对指数β定义一个学习结束时达到1的时间表。在实际中,使β从初始值β0线性退火到1。注意该超参数的选择与优先级指数α的选择是相互影响的,同时增加这两个参数会使得优先级采样更具侵略性的同时也更强烈的校正采样。
在非线性函数近似(如深度神经网络)环境下,重要度抽样与优先级回放相结合还有另一个好处:在这种情况下,大的步长可能会造成很大的破坏,因为梯度的一阶近似只在局部是可靠的,必须用较小的全局步长来防止。而在本文的方法中,优先化可以确保多次观察高误差的转移,而IS校正降低了梯度大小(从而降低了参数空间中的有效步长),并允许算法遵循高度非线性优化景观的曲率,因为泰勒展开式不断被重新近似。
我们将我们的优先级回放算法结合进一个完整的强化学习代理,基于最先进的双DQN算法。主要改进是将双DQN使用的均匀随机抽样替换为随机优先级和重要性抽样方法(见算法1)。

10.3 ATARI实验结果
参考文献
- Schaul, T., et al. Prioritized Experience Replay. arXiv e-prints, 2016.



