一、什么是宏函数?通过宏定义的函数是宏函数。如下,编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
C语言如何定义宏函数?
小九格物
c语言
在C语言中,宏函数是通过预处理器定义的,它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为,但它们不是真正的函数,因为它们在编译时不会进行类型检查,也不会分配存储空间。宏函数的定义通常使用#define指令,后面跟着宏的名称和参数列表,以及宏展开后的代码。宏函数的定义方式:1.基本宏函数:这是最简单的宏函数形式,它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
我校举行新老教师师徒结对仪式暨名师专业工作室工作交流活动
李蕾1229
为促进我校教师专业发展,发挥骨干教师的引领带头作用,11月6日下午,我校举行新老教师师徒结对仪式暨名师专业工作室工作交流活动。图片发自App会议由教师发展处李蕾主任主持,首先,由范校长宣读新老教师结对名单及双方承担职责。随后,两位新调入教师陈玉萍、莫正杰分别和他们的师傅鲍元美、刘召彬老师签订了师徒结对协议书。图片发自App图片发自App师徒拥抱、握手。有了师傅就有了目标有了方向,相信两位新教师在师
ARM驱动学习之5 LEDS驱动
JT灬新一
嵌入式C底层arm开发学习单片机
ARM驱动学习之5LEDS驱动知识点:•linuxGPIO申请函数和赋值函数–gpio_request–gpio_set_value•三星平台配置GPIO函数–s3c_gpio_cfgpin•GPIO配置输出模式的宏变量–S3C_GPIO_OUTPUT注意点:DRIVER_NAME和DEVICE_NAME匹配。实现步骤:1.加入需要的头文件://Linux平台的gpio头文件#include//三
每天都有“小感动”
河北张海霞
上次开学,在楼道值班儿的我,回到办公室后,发现我的办公桌上了一个小饭盒,打开一看,是自家腌的萝卜片,闻起来香香的,是哪位有心的孩子带来的?我猜测着……会不会是杨同学,记得开学第一天,她胃疼再加上低血糖,我曾陪她去医务室看病,并给她带回了早餐……还是李同学,那次她被别的同学欺侮,我为她主持公道。晚餐时间到了,我还带她去餐厅吃饭,引得同学们一阵羡慕……会不会是王同学,那次她眼睛不好,我陪她聊天,关心地
红手套节 马小媛为中国城市环卫者公益发声:今天我手红
疏狂君
#红手套节#公益活动,线头公益以及同多方资源的共同努力我们邀请到了线头公益大使马小媛马小媛,1993年5月3日出生于江苏省南京市,中国内地新生代女演员。2015年马小媛参演网剧《余罪》,饰演警校校花安嘉璐的闺蜜。2016年马小媛主演系列电影《丽人保镖》中女一号林欢馨,正式出道。此后,马小媛陆续接演了电视剧《警花与警犬2》,在网剧《你美丽李美丽》中担任女主角李美丽。拂晓,当你还在睡梦中时,这座城跟你
2019-03-24
李飞720
姓名:李飞企业名称:临沂鑫道食品有限公司组别373期利他1组日精进打卡第338天】【知~学习】1、阿米巴经营一段2、活用人才1段3、活法、一段【行~实践】一、修身:读书、抽烟减量、俯卧撑个跑步3公里二、齐家、劝说老爸与姑姑和好三、建功、业务洽谈【经典名句分享】1、依据原理原则追求事物的本质,以“作为人,何谓正确”进行判断2、经营者必须为员工物质和精神两方面的幸福殚精竭虑,倾尽全力,必须超脱私心,让
离奇的投毒案(七)
蜗居山人
(接上文)庭审很快开始了,李妹坐在旁听席的第一排,她想看看丈夫到底是不是害死儿女的凶手。公诉人宣读起诉书后,审判长询问张春对起诉书指控的犯罪事实是否承认,张春矢口否认,当庭翻供。李妹心中一阵得意:“我早就判断丈夫不是凶手!刑警队弄错了,这下看武队长如何收场!这可是公开审理。”审判长问:“你怎么在公安机关承认犯罪事实呢?”“他们刑讯逼供,没有办法我只能承认。”李妹心里嘟囔:“俺丈夫爱我和孩子胜过爱他
《相面天师》第二百七十章 血书
先峰老师
跟着儿子进到房间后,李云峰不满的说道:“宋老年龄都那么大了,我说你小子就不会好好和别人说话?”就是不冲着老爷子的财富地位,那年龄也值得年轻人尊重的啊,知道李尚鸿秉性的人不会说什么,但不知道的还以为老李家没家教呢。“爸,想让人尊敬,可不是件容易的事,那老头创业之初,手上没少沾血,我凭什么尊重他啊?”李尚鸿撇了撇嘴,他虽然不知道宋世豪的发家史,但是从宋世豪早年的面相中能看得出来,这老头也不是个善茬。只
27岁儿子不结婚,父亲决定先给自己相亲找个伴:我要给儿子打个样
清白路人
你妈逼你结婚了吗?现在的年轻人普遍结婚都比较晚,有的三十好几了八字还没一撇,这个时候最操心的就是父母了,他们话里话外都是催促着子女找对象结婚,甚至还会用出让人意想不到的方法,其实说到底,这也是可怜天下父母心呐。亲自给儿子打样的大爷李荣国,54岁,离异,打工收入2000多左右,家住农村平房120平。李大爷年轻时一直在工厂和工地打工,4年前才回到村里在镇政府当起了保安。李大爷的收入来自于三个部分,第一
李克富 | 咨询师推荐阅读书目
李克富
最重要的书籍不是别人的推荐,而是自己学过的教材,不论当初使用的是哪个版本,它都是我们专业的底层代码,具有不可替代性。前不久,中国心理咨询师筹委会的一位老师邀请我罗列一个推荐书目清单作为咨询师工具包的内容,并要求“说明一下简单的分类或者作三言两语的说明”。斟酌后,我觉得自己推荐的书目大体可以分为普及类书籍、心理学书籍和心理咨询与治疗专业书籍,第三类又分为适合于咨询师新手的和有经验咨询师的。经过严格筛
鲁西南方言杂谈-麻胡
一两茶叶
《汉语词典》给“麻胡”的解释是“拼音máhú,传说中人名。说法不一,以残暴著称。民间习用以恐吓小儿。谓貌丑而多须者。”的意思;《国语辞典》也给出其“传说中的坏人,用来吓唬啼哭中的小孩。也称为‘麻虎子’、‘马虎子’。唐代李匡义《资暇集.卷下.非麻胡》俗怖婴儿曰:‘麻胡来!’不知其源者,以为多髯之神而验刺者,非也。隋将军麻祜,性酷虐,炀帝令开汴河,威棱既盛,至稚童望风而畏,互相恐吓曰:‘麻祜来!’稚童
李小珍嵩县焦点初级班二期坚持分享第8天2019.3.6
快乐的老黄牛
换一个角度思考--没有一件事只有负面意义当我们遭遇困境时,往往将眼光集中在所失去或是不好的部分,殊不知,每件事的发生都是上天给我们的礼物,只是有的礼物包装得丑陋,不合你的意或是让你的情绪低落,感到挫败罢了。很多事情都不是我们看到,所听到的那样,换种角度去思维,去看事情,会见到不同或是较深层次的那样?
《相面天师》第六百七十一章 能动了
先峰老师
庄孝贤的修为之前虽然比李尚鸿差上一线,但实在是相差无几,他平日里在这聚灵阵中修炼的时候,都要控制自己吸收元气的速度,以防肉体承受不住。但是此刻李尚鸿的作为,简直就是在掠夺这些天地元气,那气势如同长鲸吸水一般,很快就将整个聚灵阵范围内的灵气席卷而尽。将别墅内聚灵阵中的灵气吸收殆尽后,李尚鸿的元神似乎壮大了一分。不过这些灵气显然不足以让它满足,那团无形无色的元神居然纵身一跃,来到了观景台的龙口之处。观
深度 Qlearning:在直播推荐系统中的应用
AGI通用人工智能之禅
程序员提升自我硅基计算碳基计算认知计算生物计算深度学习神经网络大数据AIGCAGILLMJavaPython架构设计Agent程序员实现财富自由
深度Q-learning:在直播推荐系统中的应用关键词:深度Q-learning,强化学习,直播推荐系统,个性化推荐1.背景介绍1.1问题的由来随着互联网技术的飞速发展,直播平台如雨后春笋般涌现。面对海量的直播内容,用户很难快速找到自己感兴趣的内容。因此,个性化推荐系统在直播平台中扮演着越来越重要的角色。1.2研究现状目前,主流的个性化推荐算法包括协同过滤、基于内容的推荐等。这些方法在一定程度上缓
正念内观练习20220622
蓝空静云
夏一、善念&感谢女儿一边说想明天放学后去看看要去北京手术的闺蜜,又一边念叨明天闺蜜要出发,家里得收拾行李什么的,是不是去了会添乱,真是个心思细腻又善解人意的姑娘。上周表姐回了趟老家,妈妈托给捎回来一些鹅蛋、鸡蛋还有自己腌的咸鸭蛋,拿回来一直放在楼下,今天拿上来收拾整理放入冰箱保鲜慢慢吃。妈妈家不养家畜,这些都是邻居们自家养的送给妈妈,妈妈又特意捎给女儿,妈妈总说自家养的比外面卖的好,好的总是会留给
个人学习笔记7-6:动手学深度学习pytorch版-李沐
浪子L
深度学习深度学习笔记计算机视觉python人工智能神经网络pytorch
#人工智能##深度学习##语义分割##计算机视觉##神经网络#计算机视觉13.11全卷积网络全卷积网络(fullyconvolutionalnetwork,FCN)采用卷积神经网络实现了从图像像素到像素类别的变换。引入l转置卷积(transposedconvolution)实现的,输出的类别预测与输入图像在像素级别上具有一一对应关系:通道维的输出即该位置对应像素的类别预测。13.11.1构造模型下
学习| 积极心理学—习得性无助
benignHu
习得性无助——不知不觉,你居然习得了可怕的无助,从此,它将长久伴随着你,轻易不肯离去。“习得性无助”是积极心理学之父塞利格曼的研究成果,其概念由其提出。也正是因为“习得性无助”的发现,才有后来的积极心理学,所以今天我们来好好聊聊何谓习得性无助,如何走出习得性无助。01、习得性无助一、习得性无助的由来习得性无助源于经典心理学实验:美国著名心理学家、教育心理学的创始人爱德华·李·桑代克是一个科学心理学
安全演练有保障,专项督查促改进——记公道中学校园安全(化学实验)系列活动
公中盛传云
近期,公道中学为了全面贯彻落实“预防为主,安全第一,综合治理”的安全工作方针,学校按照安全工作方针的要求,通过多种途径开展了以“预防演练为主,人防物防技防相结合”的主题的安全教育系列活动。11月8日,在学校校务会议上,学校党总支书记李兆兵强调,学校必须采取有力措施,不断增强教师综治安全防范意识,落实学校安全工作责任制,切实保障教师和学生的安全坚决杜绝意外事故的发生,确保校园平安稳定、教育教学工作顺
2021-10-22
c6a82911a6e5
致良知线上正心班学习第11天时间:2021年10月21日姓名:李克聪地区:山东淄博志愿:修己度人,自省利他|当|下|即|未|来|【自省利他致良知】今日功课1、读原文✔:2分2、准时交功课✔:2分3、日行一善✔:2分4、每日自省✔:2分(1)时刻保持恩悲敬(2)不抱怨,不说谎5、读书践行心得✔:2分菩萨为因,凡夫为果,因上努力,成果必达。自然的规律是天道,人和自然的规律是一样的。我们平时经常讲做人做
2021-04-06
四叶草_add9
中原焦点团队李金梅坚持分享第549天2021.4.6凌晨两点多忽然被乳腺疼痛惊醒,上完课后我便去了医院,结果显示三级,预约了穿刺。乳腺疾病与情绪和压力紧密相关,看来是身体向我发出信号了,果真比大脑更智慧。但愿这个信号发的并不算迟,给自己减减压,面对孩子,从心底里接纳吧!面对工作,不用精益求精,尽力就好。
《向西游记取育儿经》启示二拜师菩提第二部分:腾云驾雾识世界,开阔眼界宽胸怀
暖暖的初春
图片发自App李苹瑕焦点网络初级5期平顶山持续原创分享第697天2019年04月07日星期日晴《向西游记取育儿经》启示二拜师菩提第二部分:腾云驾雾识世界,开阔眼界宽胸怀这几天恰逢清明小长假,许多家长都会带领孩子祭祖扫墓和清明踏春郊游。刚好我们这一周总第31期读书会主题:腾云驾雾识世界,开阔眼界宽胸怀。描述的是孙悟空成长初期师拜菩提所受到的启蒙教育,和现今各位家长注重孩子的早期成长和启蒙教育是不谋而
《兄弟》七
刘佳琪ljq
爱的力量从来不可以被低估。最近忙碌的我住在了姥姥家,第一次一个人骑着小电驴来到了姥姥家,一切都是新的,一切对我来说都是一个挑战。记得很久以前因为妈妈和姥姥发生过一次争吵,时间是在过年得时候,我匆忙离开跑到了老太太家里,那一刻的我无比的绝望,也认识到了自己的错误。今天的我再次想起这件事情时,内心充满了愧疚感,父母之爱子,则为之计深远。李光头的母亲李兰一直在为自己的儿子着想,离去前还在叮嘱宋钢照顾李光
2003-7-13-先胜“李一季”-(让左车马-黑列手炮)
夏目青樱
2003-7-13-【虎滩四战之三】先胜“李一季”-(让左车马-黑列手炮)1.炮二平五炮2平52.马二进三马8进73.兵三进一炮8进44.车一进一炮8平75.相三进一马2进36.兵七进一车1平27.炮八平七卒5进18.车一平四马3进5?9.车四进二炮7平510.车四平五车2进7?!11.炮五平八卒5进1?12.车五平八马5进413.炮七平五炮5进514.相七进五马4进515.车八平六车9平816.
《相面天师》第六百四十三章 死在你前面
先峰老师
说实话,安东尼马库斯的进攻套路虽然很简单,来来去去就是左右腿的侧踢。但是经过千万次的训练,安东尼马库斯已经将这扫腿练得炉火纯青,就是这简单的侧踢,最少带给李尚鸿三次以上致命的威胁。交战了大约有七八分钟的时间了,安东尼马库斯时而像是西伯利亚的猛虎,大开大合硬拼硬打,时而又像是狐狸一般,数次都逃过了李尚鸿的致命一击。虽然也对安东尼马库斯造成了一些伤害,但至今为止,李尚鸿也未能找到一击毙敌的机会,可是眼
小米和蛋壳 第七节 和三三吃饭
斜晲众生
李南还是老样子,笔直,严谨,脸上线条硬度极佳,总是一副不苟言笑的样子。身上除了黑色就是深色的搭配,把自己平添了许多收敛的气息。和旁边像精灵一样的三三真真是反差萌。“我已经点好了菜。我在微博微信上已经盯了好久了,这次点菜集各家吃货推荐所长,应该不会踩雷。点了有焖鸡,牛肉饵丝,油爆猪皮,香茅烤鸡,稀豆粉,炒小瓜,蒜香鸡脚,小锅米线,黄金虾饼,喝的除了自酿米酒、苹果芒果汁和酸角汁。三碗米饭,一份菠萝饭。
小说《101所》09:官司(中)
一言莫辩
经过合同、沙盘和现场对比,李天明觉得外部环境的变化,可以打打官司,至少还有沙盘模型作为证据,虽然合同里声明不能作为的合同的条款,但外部环境足以影响到是否购买底楼的房子,而且这是开发商提供的格式合同,该条款明显规避了开发商的责任,签订合同时没有特别的提示,李天明记得当初自学法律时,记得特别清楚,书上举的例子是保险合同的免责条款。慎重起见,李天明专门咨询了法院和律师朋友,虽然没有得到确切的答复,但是找
极品小农场 名窑 第1062章
龘龑文轩
第1062章洞穴餐厅李汉喝了口啤酒,面色严肃说道。“不说这些,赖斯,王储婚礼这件事你和尼古拉斯多用心思,今天晚上的事杰西卡你跟一下,这次要给着他们一个个狠狠的教训,这段时间,我可不想再出什么意外。”杰西卡点头,保证道。“boss,你放心,这些该死混蛋,这次一定会记住一辈子。”“不要太过,狗急跳墙,那可就不好了。”李汉说话,手指弹了下竖着小耳朵偷听的嘟嘟脑门一下。“去洗澡,睡觉。”“哦。”嘟嘟不情不
小儿推拿李波:炎炎夏日,防晒、防蚊、防扉,宝宝皮肤护理有门道
55e69701d1dd
小儿推拿李波:炎炎夏日,防晒、防蚊、防扉,宝宝皮肤护理有门道眼下,天气热湿度高,在这样的环境里,宝宝娇嫩的皮肤更容易产生问题。晒伤、长痱子、红屁股、蚊虫叮咬……诸如此类的皮肤问题困扰着不少新手爸妈。想要宝宝的皮肤健康,防晒、防蚊、防痱等“功课”家长可以提前做。小儿推拿李波:炎炎夏日,防晒、防蚊、防扉,宝宝皮肤护理有门道痱子痱子是宝宝夏季最常见的皮肤问题。夏天出汗多,喜欢活动的宝宝,最容易出汗。过多
1
知是是非
钱老师好,我是八班的李川,这是我的号,我这个号的号名没按您的来,首先,我违背了您的要求,给您和和同学们带来的不便,我深感抱歉。其次,我之所以没按您的要求来是因为我想以号名为我的笔名,虽然我写的作文从来从来都没超过45分,一直以来都是我自己写完也不想去看,但我还是很喜欢写作文。所以我郑重其事的给我自己起了个笔名,本来开始我想用“我想上树”这个笔名的,这是因为我小时候很喜欢爬树但却因为种种原因我很少能
Enum 枚举
120153216
enum枚举
原文地址:http://www.cnblogs.com/Kavlez/p/4268601.html Enumeration
于Java 1.5增加的enum type...enum type是由一组固定的常量组成的类型,比如四个季节、扑克花色。在出现enum type之前,通常用一组int常量表示枚举类型。比如这样:
public static final int APPLE_FUJI = 0
Java8简明教程
bijian1013
javajdk1.8
Java 8已于2014年3月18日正式发布了,新版本带来了诸多改进,包括Lambda表达式、Streams、日期时间API等等。本文就带你领略Java 8的全新特性。
一.允许在接口中有默认方法实现
Java 8 允许我们使用default关键字,为接口声明添
Oracle表维护 快速备份删除数据
cuisuqiang
oracle索引快速备份删除
我知道oracle表分区,不过那是数据库设计阶段的事情,目前是远水解不了近渴。
当前的数据库表,要求保留一个月数据,且表存在大量录入更新,不存在程序删除。
为了解决频繁查询和更新的瓶颈,我在oracle内根据需要创建了索引。但是随着数据量的增加,一个半月数据就要超千万,此时就算有索引,对高并发的查询和更新来说,让然有所拖累。
为了解决这个问题,我一般一个月会进行一次数据库维护,主要工作就是备
java多态内存分析
麦田的设计者
java内存分析多态原理接口和抽象类
“ 时针如果可以回头,熟悉那张脸,重温嬉戏这乐园,墙壁的松脱涂鸦已经褪色才明白存在的价值归于记忆。街角小店尚存在吗?这大时代会不会牵挂,过去现在花开怎么会等待。
但有种意外不管痛不痛都有伤害,光阴远远离开,那笑声徘徊与脑海。但这一秒可笑不再可爱,当天心
Xshell实现Windows上传文件到Linux主机
被触发
windows
经常有这样的需求,我们在Windows下载的软件包,如何上传到远程Linux主机上?还有如何从Linux主机下载软件包到Windows下;之前我的做法现在看来好笨好繁琐,不过也达到了目的,笨人有本方法嘛;
我是怎么操作的:
1、打开一台本地Linux虚拟机,使用mount 挂载Windows的共享文件夹到Linux上,然后拷贝数据到Linux虚拟机里面;(经常第一步都不顺利,无法挂载Windo
类的加载ClassLoader
肆无忌惮_
ClassLoader
类加载器ClassLoader是用来将java的类加载到虚拟机中,类加载器负责读取class字节文件到内存中,并将它转为Class的对象(类对象),通过此实例的 newInstance()方法就可以创建出该类的一个对象。
其中重要的方法为findClass(String name)。
如何写一个自己的类加载器呢?
首先写一个便于测试的类Student
html5写的玫瑰花
知了ing
html5
<html>
<head>
<title>I Love You!</title>
<meta charset="utf-8" />
</head>
<body>
<canvas id="c"></canvas>
google的ConcurrentLinkedHashmap源代码解析
矮蛋蛋
LRU
原文地址:
http://janeky.iteye.com/blog/1534352
简述
ConcurrentLinkedHashMap 是google团队提供的一个容器。它有什么用呢?其实它本身是对
ConcurrentHashMap的封装,可以用来实现一个基于LRU策略的缓存。详细介绍可以参见
http://code.google.com/p/concurrentlinke
webservice获取访问服务的ip地址
alleni123
webservice
1. 首先注入javax.xml.ws.WebServiceContext,
@Resource
private WebServiceContext context;
2. 在方法中获取交换请求的对象。
javax.xml.ws.handler.MessageContext mc=context.getMessageContext();
com.sun.net.http
菜鸟的java基础提升之道——————>是否值得拥有
百合不是茶
1,c++,java是面向对象编程的语言,将万事万物都看成是对象;java做一件事情关注的是人物,java是c++继承过来的,java没有直接更改地址的权限但是可以通过引用来传值操作地址,java也没有c++中繁琐的操作,java以其优越的可移植型,平台的安全型,高效性赢得了广泛的认同,全世界越来越多的人去学习java,我也是其中的一员
java组成:
通过修改Linux服务自动启动指定应用程序
bijian1013
linux
Linux中修改系统服务的命令是chkconfig (check config),命令的详细解释如下: chkconfig
功能说明:检查,设置系统的各种服务。
语 法:chkconfig [ -- add][ -- del][ -- list][系统服务] 或 chkconfig [ -- level <</SPAN>
spring拦截器的一个简单实例
bijian1013
javaspring拦截器Interceptor
Purview接口
package aop;
public interface Purview {
void checkLogin();
}
Purview接口的实现类PurviesImpl.java
package aop;
public class PurviewImpl implements Purview {
public void check
[Velocity二]自定义Velocity指令
bit1129
velocity
什么是Velocity指令
在Velocity中,#set,#if, #foreach, #elseif, #parse等,以#开头的称之为指令,Velocity内置的这些指令可以用来做赋值,条件判断,循环控制等脚本语言必备的逻辑控制等语句,Velocity的指令是可扩展的,即用户可以根据实际的需要自定义Velocity指令
自定义指令(Directive)的一般步骤
&nbs
【Hive十】Programming Hive学习笔记
bit1129
programming
第二章 Getting Started
1.Hive最大的局限性是什么?一是不支持行级别的增删改(insert, delete, update)二是查询性能非常差(基于Hadoop MapReduce),不适合延迟小的交互式任务三是不支持事务2. Hive MetaStore是干什么的?Hive persists table schemas and other system metadata.
nginx有选择性进行限制
ronin47
nginx 动静 限制
http {
limit_conn_zone $binary_remote_addr zone=addr:10m;
limit_req_zone $binary_remote_addr zone=one:10m rate=5r/s;...
server {...
location ~.*\.(gif|png|css|js|icon)$ {
java-4.-在二元树中找出和为某一值的所有路径 .
bylijinnan
java
/*
* 0.use a TwoWayLinkedList to store the path.when the node can't be path,you should/can delete it.
* 1.curSum==exceptedSum:if the lastNode is TreeNode,printPath();delete the node otherwise
Netty学习笔记
bylijinnan
javanetty
本文是阅读以下两篇文章时:
http://seeallhearall.blogspot.com/2012/05/netty-tutorial-part-1-introduction-to.html
http://seeallhearall.blogspot.com/2012/06/netty-tutorial-part-15-on-channel.html
我的一些笔记
===
js获取项目路径
cngolon
js
//js获取项目根路径,如: http://localhost:8083/uimcardprj
function getRootPath(){
//获取当前网址,如: http://localhost:8083/uimcardprj/share/meun.jsp
var curWwwPath=window.document.locati
oracle 的性能优化
cuishikuan
oracleSQL Server
在网上搜索了一些Oracle性能优化的文章,为了更加深层次的巩固[边写边记],也为了可以随时查看,所以发表这篇文章。
1.ORACLE采用自下而上的顺序解析WHERE子句,根据这个原理,表之间的连接必须写在其他WHERE条件之前,那些可以过滤掉最大数量记录的条件必须写在WHERE子句的末尾。(这点本人曾经做过实例验证过,的确如此哦!
Shell变量和数组使用详解
daizj
linuxshell变量数组
Shell 变量
定义变量时,变量名不加美元符号($,PHP语言中变量需要),如:
your_name="w3cschool.cc"
注意,变量名和等号之间不能有空格,这可能和你熟悉的所有编程语言都不一样。同时,变量名的命名须遵循如下规则:
首个字符必须为字母(a-z,A-Z)。
中间不能有空格,可以使用下划线(_)。
不能使用标点符号。
不能使用ba
编程中的一些概念,KISS、DRY、MVC、OOP、REST
dcj3sjt126com
REST
KISS、DRY、MVC、OOP、REST (1)KISS是指Keep It Simple,Stupid(摘自wikipedia),指设计时要坚持简约原则,避免不必要的复杂化。 (2)DRY是指Don't Repeat Yourself(摘自wikipedia),特指在程序设计以及计算中避免重复代码,因为这样会降低灵活性、简洁性,并且可能导致代码之间的矛盾。 (3)OOP 即Object-Orie
[Android]设置Activity为全屏显示的两种方法
dcj3sjt126com
Activity
1. 方法1:AndroidManifest.xml 里,Activity的 android:theme 指定为" @android:style/Theme.NoTitleBar.Fullscreen" 示例: <application
solrcloud 部署方式比较
eksliang
solrCloud
solrcloud 的部署其实有两种方式可选,那么我们在实践开发中应该怎样选择呢? 第一种:当启动solr服务器时,内嵌的启动一个Zookeeper服务器,然后将这些内嵌的Zookeeper服务器组成一个集群。 第二种:将Zookeeper服务器独立的配置一个集群,然后将solr交给Zookeeper进行管理
谈谈第一种:每启动一个solr服务器就内嵌的启动一个Zoo
Java synchronized关键字详解
gqdy365
synchronized
转载自:http://www.cnblogs.com/mengdd/archive/2013/02/16/2913806.html
多线程的同步机制对资源进行加锁,使得在同一个时间,只有一个线程可以进行操作,同步用以解决多个线程同时访问时可能出现的问题。
同步机制可以使用synchronized关键字实现。
当synchronized关键字修饰一个方法的时候,该方法叫做同步方法。
当s
js实现登录时记住用户名
hw1287789687
记住我记住密码cookie记住用户名记住账号
在页面中如何获取cookie值呢?
如果是JSP的话,可以通过servlet的对象request 获取cookie,可以
参考:http://hw1287789687.iteye.com/blog/2050040
如果要求登录页面是html呢?html页面中如何获取cookie呢?
直接上代码了
页面:loginInput.html
代码:
<!DOCTYPE html PUB
开发者必备的 Chrome 扩展
justjavac
chrome
Firebug:不用多介绍了吧https://chrome.google.com/webstore/detail/bmagokdooijbeehmkpknfglimnifench
ChromeSnifferPlus:Chrome 探测器,可以探测正在使用的开源软件或者 js 类库https://chrome.google.com/webstore/detail/chrome-sniffer-pl
算法机试题
李亚飞
java算法机试题
在面试机试时,遇到一个算法题,当时没能写出来,最后是同学帮忙解决的。
这道题大致意思是:输入一个数,比如4,。这时会输出:
&n
正确配置Linux系统ulimit值
字符串
ulimit
在Linux下面部 署应用的时候,有时候会遇上Socket/File: Can’t open so many files的问题;这个值也会影响服务器的最大并发数,其实Linux是有文件句柄限制的,而且Linux默认不是很高,一般都是1024,生产服务器用 其实很容易就达到这个数量。下面说的是,如何通过正解配置来改正这个系统默认值。因为这个问题是我配置Nginx+php5时遇到了,所以我将这篇归纳进
hibernate调用返回游标的存储过程
Supanccy2013
javaDAOoracleHibernatejdbc
注:原创作品,转载请注明出处。
上篇博文介绍的是hibernate调用返回单值的存储过程,本片博文说的是hibernate调用返回游标的存储过程。
此此扁博文的存储过程的功能相当于是jdbc调用select 的作用。
1,创建oracle中的包,并在该包中创建的游标类型。
---创建oracle的程
Spring 4.2新特性-更简单的Application Event
wiselyman
application
1.1 Application Event
Spring 4.1的写法请参考10点睛Spring4.1-Application Event
请对比10点睛Spring4.1-Application Event
使用一个@EventListener取代了实现ApplicationListener接口,使耦合度降低;
1.2 示例
包依赖
<p
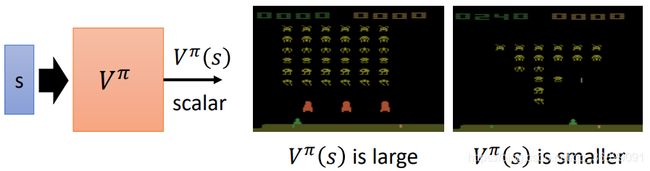
![]() ,评价它的好坏。
,评价它的好坏。![]() ,代表在遇到游戏的某个 state 后,采取策略
,代表在遇到游戏的某个 state 后,采取策略 ![]() 一直玩到游戏结束,所能得到的 reward 之和。
一直玩到游戏结束,所能得到的 reward 之和。![]() (即critic)是个函数,一个网络(前两讲提到 actor 同样是个网络)。它的输入是某个state,输出是一个scalar标量。上图游戏画面中左边的
(即critic)是个函数,一个网络(前两讲提到 actor 同样是个网络)。它的输入是某个state,输出是一个scalar标量。上图游戏画面中左边的 ![]() 很大,因为当前怪物比较多,防护罩也没被摧毁,从此时玩到游戏结束得到的 reward 就会比较多;而相对的右边的
很大,因为当前怪物比较多,防护罩也没被摧毁,从此时玩到游戏结束得到的 reward 就会比较多;而相对的右边的 ![]() 就比较小。综上 critic 的输出取决于两点:1是 state,2是 actor 的策略
就比较小。综上 critic 的输出取决于两点:1是 state,2是 actor 的策略 ![]() 。
。![]() ,在
,在 ![]() 的情况下,网络输出为
的情况下,网络输出为 ![]() (代表预测的 reward);而实际得到的 reward 为
(代表预测的 reward);而实际得到的 reward 为 ![]() 。我们的目标就是让
。我们的目标就是让 ![]() 和
和 ![]() 尽可能接近,这其实和 regression problem 很相似。
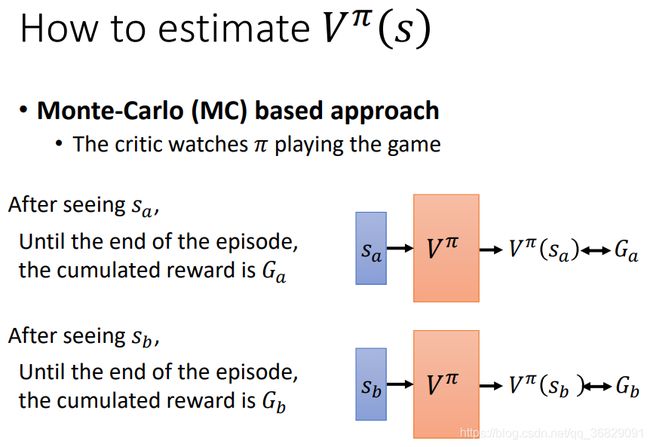
尽可能接近,这其实和 regression problem 很相似。![]() 玩到
玩到 ![]() 就行。因为
就行。因为 ![]() ,即 :
,即 :![]() 状态下采取策略
状态下采取策略 ![]() 玩完游戏得到的 value =
玩完游戏得到的 value = ![]() 状态下采取策略
状态下采取策略 ![]() 玩完游戏得到的 value + 执行动作
玩完游戏得到的 value + 执行动作 ![]() 得到的单步
得到的单步 ![]()
![]() 和
和 ![]() 间的接近程度即可。
间的接近程度即可。![]() 的方差很大(回顾一下,
的方差很大(回顾一下, ![]() 在
在 ![]() 的情况下根据策略
的情况下根据策略 ![]() 进行游戏得到的实际 reward. 其实是一个随机变量,因为游戏是有随机性的,每一次得到
进行游戏得到的实际 reward. 其实是一个随机变量,因为游戏是有随机性的,每一次得到 ![]() 是不一样的)。
是不一样的)。![]() 是很多步 reward 的求和,而根据公式
是很多步 reward 的求和,而根据公式 ![]() ,每一步 reward 的方差累加后的方差会乘上
,每一步 reward 的方差累加后的方差会乘上 ![]() 。所以最后
。所以最后 ![]() 的方差很大,即每次算出来的
的方差很大,即每次算出来的 ![]() 都会相差很多。
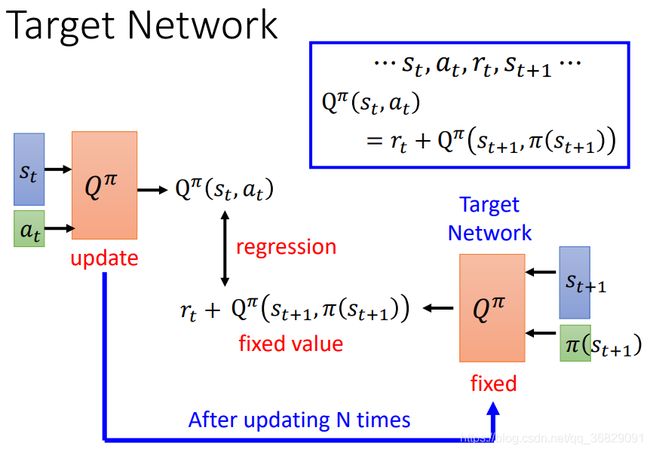
都会相差很多。![]() ,它的方差比较小。但 TD 的问题在于
,它的方差比较小。但 TD 的问题在于 ![]() 可能很不准确。以下举例说明:
可能很不准确。以下举例说明:![]() 是不一样的(可能是 3/4 或 0):
是不一样的(可能是 3/4 或 0):![]() 只在第一个 episode 中出现,出现后根据策略
只在第一个 episode 中出现,出现后根据策略 ![]() 得到的 reward 是0,所以
得到的 reward 是0,所以 ![]() =0
=0![]() 只在第一个 episode 中出现,而
只在第一个 episode 中出现,而 ![]() 出现后跳到了
出现后跳到了 ![]() ,所以
,所以 ![]() .
.![]() 是一个非常不好的 state,出现
是一个非常不好的 state,出现 ![]() 后
后 ![]() 被影响只得到 0 的 reward,所以认为
被影响只得到 0 的 reward,所以认为 ![]() 为0.
为0.![]() 后
后 ![]() 得到 reward 为 0 只是一个巧合,与
得到 reward 为 0 只是一个巧合,与 ![]() 无关,大部分情况下
无关,大部分情况下 ![]() 还是会得到 3/4 的 reward,所以认为
还是会得到 3/4 的 reward,所以认为 ![]() 为3/4。(因为Sb在Sa之后)
为3/4。(因为Sb在Sa之后)![]() 的 Q function
的 Q function ![]() ,就能有办法找到一个更好的 actor
,就能有办法找到一个更好的 actor ![]() ,这样就能不断更新policy
,这样就能不断更新policy ![]() 。
。![]() 比 π 好呢?
比 π 好呢?![]() 得到的 value 一定比使用策略
得到的 value 一定比使用策略 ![]() 得到的 value 大,即:
得到的 value 大,即:![]()
![]() 的方法是,对于已经学到的 Q function
的方法是,对于已经学到的 Q function ![]() ,在某个给定的 state 下,分别带入可能的 action,看看哪一个 action 使得函数值最大,把使得函数值最大的 a,作为以后面对该 state 时采取的 action。
,在某个给定的 state 下,分别带入可能的 action,看看哪一个 action 使得函数值最大,把使得函数值最大的 a,作为以后面对该 state 时采取的 action。![]() :TODO
:TODO