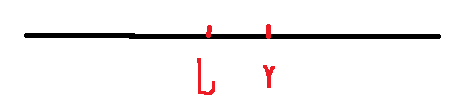2022年java A组考后总结
文章目录
-
- 试题 **A:** 裁纸刀
- 试题 **B:** 寻找整数
- 试题 **C:** 求和
- 试题 **D**: GCD
- 试题 **E:** 蜂巢
- 试题 **F:** 全排列的价值
- 试题 **G:** 青蛙过河
- 试题 **H:** 因数平方和
- 试题 **I:** 最优清零方案
- 试题 **J:** 推导部分和
备考这么久终于是考完了,感觉题挺难的,填空两个都不太会,然后大题中蜂巢看了不太向做就跳了,还有两三个是暴力解法的,其他的题目给的测试用例都过了,自己编了几个小的也都过了,但是不知道比较大的测试用例怎么样
无论这次比赛做的怎么样,希望大家都不要气馁,这只是开始,并不是结束,不要把刷题当成一种压力,应该慢慢把他当成一种习惯,刷题多了就会发现看了题目后很快就能和曾经做过的题联系起来,然后得到答案
这篇文章写来回顾考试过程,答案不确保正确,欢迎大佬评论区指正
如果需要题目可以评论区发邮箱
试题 A: 裁纸刀
这个题感觉自己是做错了,我是直接 4 + 21 + 19 ∗ 22 = 443 4 + 21 + 19 * 22 = 443 4+21+19∗22=443了,也就是先裁周围的边,然后把22那个边裁掉,然后再把剩下的裁掉
回来和同学讨论了一下感觉应该是每次都裁剩余边里面的最长边
比如这个题开始是 20 ∗ 22 20*22 20∗22的,那么第一次裁剪完变成两个 20 ∗ 11 20 *11 20∗11的,第二次裁剪完变成四个 10 ∗ 11 10*11 10∗11的,这样递推下去,最后得到结果
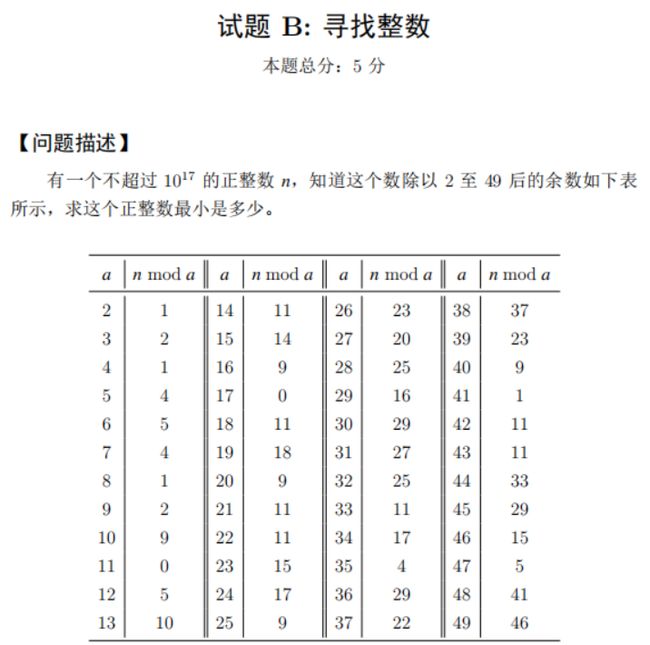
试题 B: 寻找整数
不会,当时暴力搜索,开始时46,后面每次加49,运行了半个小时搜索到13次方了,就停掉了,感觉答案在16次方左右,搜到答案还得 30 ∗ 1000 30*1000 30∗1000分钟,没意义
试题 C: 求和
这个题直接模拟做的,但是看他的数据范围感觉有些数据要超时了
package code;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class exerC {
static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer in = new StreamTokenizer(bf);
static int nextInt() throws IOException {
in.nextToken();
return (int) in.nval;
}
public static void main(String[] args) throws IOException {
int n = nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = nextInt();
}
// 处理数据
long ans = 0;
for (int i = 0; i < arr.length; i++) {
for (int j = i + 1; j < arr.length; j++) {
ans += arr[i] * arr[j];
}
}
System.out.println(ans);
}
}
试题 D: GCD
这个也暴力搜索的,但是不知道终止大小设置多少,我这里取的是两个中较大的值,但是也想不到什么理论依据
package code;
import java.util.Scanner;
public class exerD {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int a = sc.nextInt();
int b = sc.nextInt();
sc.close();
int ansK = 0;
int maxGCD = 0;
int end = Math.max(a, b);
for (int i = 1; i < end; i++) {
int temp = gcd(a + i, b + i);
if (temp > maxGCD) {
ansK = i;
maxGCD = temp;
}
}
System.out.println(ansK);
}
private static int gcd(int a, int b) {
return a % b == 0 ? b : gcd(b, a % b);
}
}
试题 E: 蜂巢
这个当时看了一下,感觉是bfs,然后就跳了,后面写完回来不想写了。。。
试题 F: 全排列的价值
这个题我的这个解法比较巧妙,用的数学推导找出来规律做的
具体详细思路后面更新
package code;
import java.util.Scanner;
public class exerF {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
sc.close();
if (n == 0 || n == 1) {
System.out.println(0);
return;
}
long preNum = 2;
long preCount = 1;
for (int i = 3; i <= n; i++) {
preCount = ((preNum * i * (i - 1) / 2) % 998244353 + (preCount * i) % 998244353) % 998244353;
preNum = (i * preNum) % 998244353;
}
System.out.println(preCount);
}
}
试题 G: 青蛙过河
这个题我用的是二分+贪心,二分就列举所有的可能性,就不细说了
然后贪心的想法是,先找比较远的跳,如果能调远的就不跳近的(感觉不靠谱),如果远的调不了就一直减一,直到能调或者跳不了为止
这个题没有很大把握,可能就直接是错的,剩下半小时才写了hhh,不过还是过了自己的几个简单的测试用例,应该能骗一点分吧
package code;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class exerG {
static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer in = new StreamTokenizer(bf);
static int nextInt() throws IOException {
in.nextToken();
return (int) in.nval;
}
public static void main(String[] args) throws IOException {
int n = nextInt();
int x = nextInt();
int[] arr = new int[n - 1];
for (int i = 0; i < arr.length; i++) {
arr[i] = nextInt();
}
int l = 1;
int r = n;
int ans = 0;
while (l <= r) {
int mid = (r - l) / 2 + l;
if (check(mid, arr.clone(), x)) {
ans = mid;
r = mid - 1;
} else {
l = mid + 1;
}
}
System.out.println(ans);
}
private static boolean check(int mid, int[] arr, int x) {
// 如果可以跳过去返回true,否则返回false
for (int i = 0; i < x; i++) {
// 跳过去
int begin = -1;
while (begin < arr.length) {
int tempStep = mid;
while (begin + tempStep < arr.length && tempStep != 0 && arr[begin + tempStep] == 0) {
tempStep--;
}
if (begin + tempStep >= arr.length) {
break;
} else {
if (tempStep == 0) {
return false;
}
arr[begin + tempStep]--;
begin = begin + tempStep;
}
}
// 跳回来
begin = arr.length;
while (begin >= 0) {
int tempStep = mid;
while (begin - tempStep >= 0 && tempStep != 0 && arr[begin - tempStep] == 0) {
tempStep--;
}
if (begin - tempStep < 0) {
break;
} else {
if (tempStep == 0) {
return false;
}
arr[begin - tempStep]--;
begin = begin - tempStep;
}
}
}
return true;
}
}
试题 H: 因数平方和
这个题是真的坑,最后剩下40分钟了才通知测试用例给错了,搁那调试了二十多分钟都找不出来问题,人麻了
我的做法也是直接暴力解了,能过20%的用例了,自己跑 1 0 7 10^7 107的就已经三秒多了。。。
package code;
import java.util.Scanner;
public class exerH {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
sc.close();
long[] arr = new long[n + 1];
long sum = 0;
for (long i = 1; i < arr.length; i++) {
long j = i;
while (j < arr.length) {
arr[(int) j] = (arr[(int) j] + i * i) % 1000000007;
j += i;
}
sum = (sum + arr[(int) i]) % 1000000007;
}
System.out.println(sum);
}
}
试题 I: 最优清零方案
这个过会更,感觉做的没有问题
package code;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class exerI {
static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer in = new StreamTokenizer(bf);
static int nextInt() throws IOException {
in.nextToken();
return (int) in.nval;
}
public static void main(String[] args) throws IOException {
int N = nextInt();
int K = nextInt();
int[] arr = new int[N];
for (int i = 0; i < arr.length; i++) {
arr[i] = nextInt();
}
long ans = 0;
for (int i = 0; i < arr.length; i++) {
int minVal = arr[i];
for (int j = 1; j < K; j++) {
if (i + j < arr.length) {
minVal = Math.min(minVal, arr[i + j]);
} else {
minVal = 0;
break;
}
}
if (minVal != 0) {
for (int j = 0; j < K; j++) {
arr[i + j] -= minVal;
}
}
ans += minVal;
ans += arr[i];
}
System.out.println(ans);
}
}
试题 J: 推导部分和
这个题的话主要是根据输入的区间数据来确定哪些区间是可以得到的
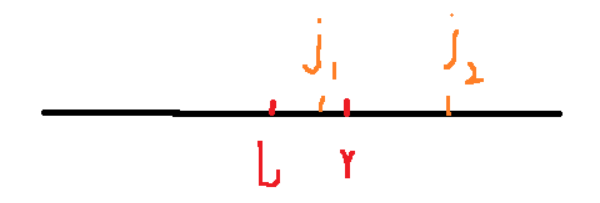
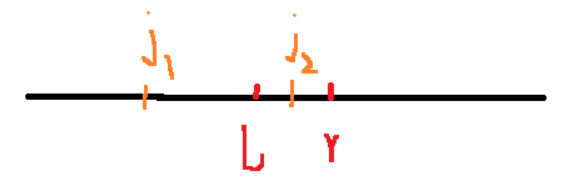
主要分为四种情况,对于下图的l和r的情况来讨论
- 如果已知 [ j , l − 1 ] [j,l-1] [j,l−1]的和,那么就可以得到 [ j , r ] [j,r] [j,r]的部分和
- 如果已知 [ l , j ] [l,j] [l,j]的部分和,这里需要分情况讨论,
- 如果j在r的左边就可以得到 [ j + 1 , r ] [j+1,r] [j+1,r]的部分和,如 j 1 j_1 j1
- 如果j在r的右边就可以得到 [ r + 1 , j ] [r+1,j] [r+1,j]的部分和,如 j 2 j_2 j2
- 如果已知 [ j , r ] [j,r] [j,r]的部分和,这里也需要分情况讨论
- 如果j在l的左边就可以得到 [ j , l − 1 ] [j,l-1] [j,l−1]的部分和
- 如果j的l的右边就可以得到 [ l , j − 1 ] [l,j-1] [l,j−1]的部分和
- 如果已知 [ r , j ] [r,j] [r,j]的部分和,就可以得到 [ l , j ] [l,j] [l,j]的部分和
后面只需要查对应对应位置有没有元素即可,如果为0则说明这里得不到,如果不为0,则说明可以求得这个区间的和
package code;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
public class exerJ {
static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer in = new StreamTokenizer(bf);
static int nextInt() throws IOException {
in.nextToken();
return (int) in.nval;
}
public static void main(String[] args) throws IOException {
int N = nextInt();
int M = nextInt();
int Q = nextInt();
int[][] knowArr = new int[N][N];
int[][] givenArr = new int[M][2];
for (int i = 0; i < givenArr.length; i++) {
int l = nextInt() - 1;
int r = nextInt() - 1;
int S = nextInt();
knowArr[l][r] = S;
// 以l为终点
if (l > 0) {
for (int j = 0; j < N && j < l; j++) {
if (knowArr[j][l - 1] != 0) {
knowArr[j][r] = knowArr[j][l - 1] + S;
}
}
}
// 以l为起点
if (l < N - 1) {
for (int j = l + 1; j < N; j++) {
if (knowArr[l][j] != 0) {
if (j < r) {
knowArr[j + 1][r] = S - knowArr[l][j];
} else if (j > r) {
knowArr[r + 1][j] = knowArr[l][j] - S;
}
}
}
}
// 以r为终点
if (r > 0) {
for (int j = 0; j < N && j < r; j++) {
if (knowArr[j][r] != 0) {
if (j < l) {
knowArr[j][l - 1] = knowArr[j][r] - S;
} else if (j > l) {
knowArr[l][j - 1] = S - knowArr[j][r];
}
}
}
}
// 以r为起点
if (r < N - 1) {
for (int j = r + 1; j < N; j++) {
if (knowArr[r][j] != 0) {
knowArr[l][j] = S + knowArr[r][j];
}
}
}
}
for (int i = 0; i < Q; i++) {
int l = nextInt() - 1;
int r = nextInt() - 1;
if (knowArr[l][r] != 0) {
System.out.println(knowArr[l][r]);
} else {
System.out.println("UNKNOWN");
}
}
}
}