原文链接:http://tecdat.cn/?p=3186
本文显示了如何基于潜在的ARMA-GARCH模型(当然也涉及更广泛意义上的QRM)来拟合和预测风险价值(VaR)。
从ARMA-GARCH过程模拟(log-return)数据
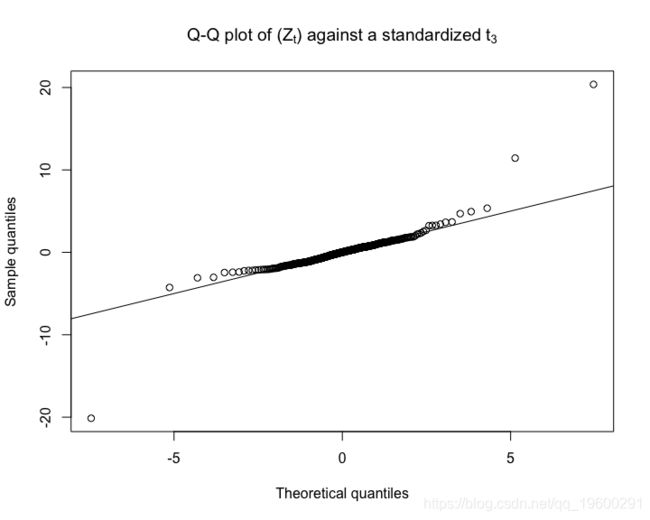
我们考虑使用t 分布的ARMA(1,1)-GARCH(1,1)过程。
模拟一个序列(用于说明目的)。
nu <- 3 fixed.p <- list(mu = 0, # mu (截距)
ar1 = 0.5, # phi\_1 (AR(1) 参数 of mu\_t)
ma1 = 0.3, # theta\_1 (MA(1) 参数 of mu\_t)
omega = 4, # alpha_0 (截距)
alpha1 = 0.4, # alpha\_1 (GARCH(1) 参数 of sigma\_t^2)
beta1 = 0.2, # beta\_1 (GARCH(1) 参数 of sigma\_t^2)
shape = nu) # armaOrder <- c(1,1) # ARMA 参数garchOrder <- c(1,1) # GARCH 参数varModel <- list(model = "sGARCH", garchOrder = garchOrder)
spec <- ugarchspec(varModel, mean.model = list(armaOrder = armaOrder),
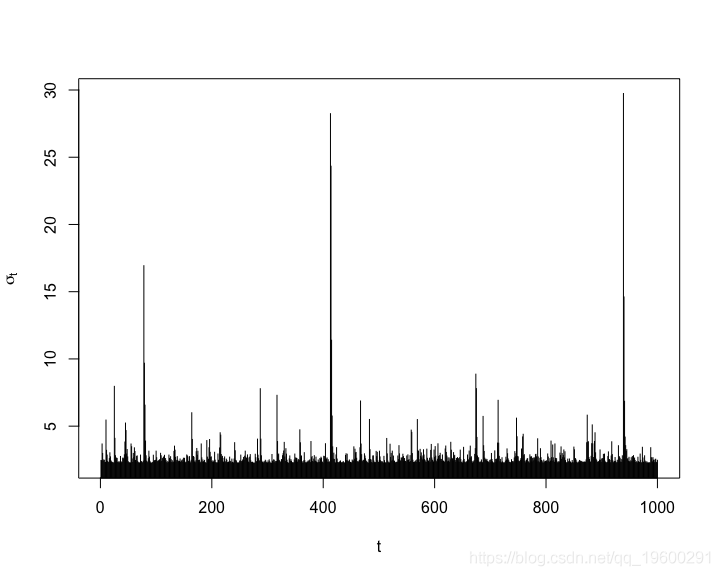
fixed.pars = fixed.p, distribution.model = "std") # t 标准残差作为一个完整性检查,让我们绘制模拟序列,条件标准偏差和残差。
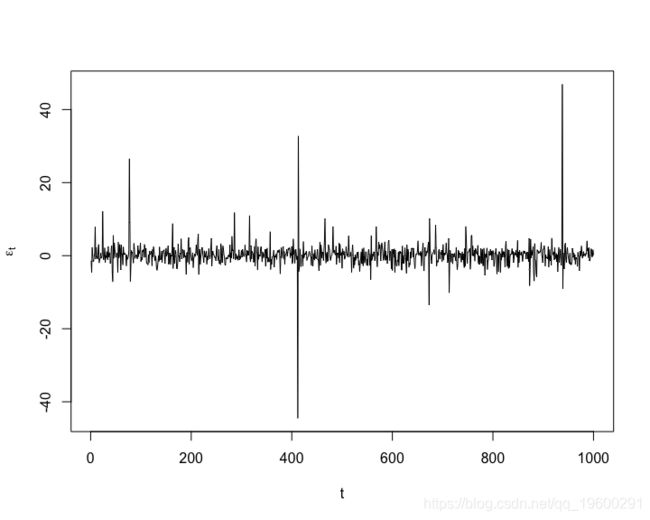
plot(X, type = "l", xlab = "t", ylab = expression(X\[t\]))
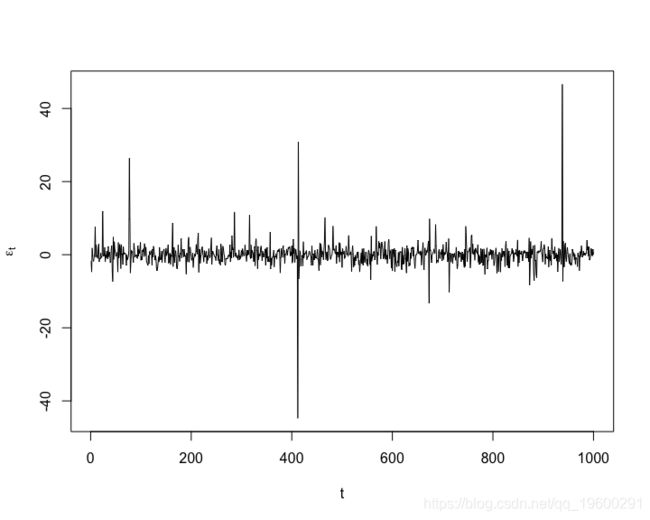
plot(sig, type = "h", xlab = "t", ylab = expression(sigma\[t\]))plot(eps, type = "l", xlab = "t", ylab = expression(epsilon\[t\]))将ARMA-GARCH模型拟合到(模拟)数据
拟合ARMA-GARCH模型 。
让我们再考虑一些健全性检查。
## 拟合 ARMA(1,1)-GARCH(1,1) model
spec <- ugarchspec(varModel, mean.model = list(armaOrder = armaOrder),
distribution.model = "std") #
fit <- ugarchfit(spec, data = X) # fit
##
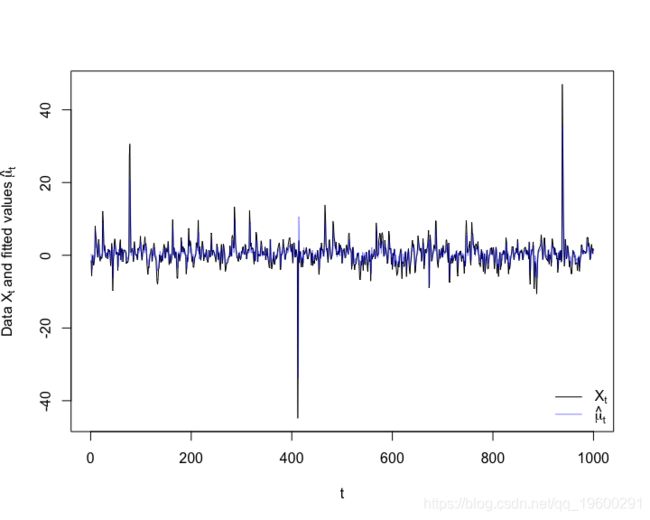
mu. <- fitted(fit) # 拟合 hat{mu}\_t (= hat{X}\_t)
sig. <- sigma(fit) # 拟合 hat{sigma}_t
##
stopifnot(all.equal(as.numeric(mu.), fit@fit$fitted.values),
all.equal(as.numeric(sig.), fit@fit$sigma))计算VaR时间序列
计算VaR估计值。请注意,我们也可以在这里使用基于GPD的估算模型。
Backtest VaR估计值
让我们回测VaR的估计。
## \[1\] 10
## \[1\] 12
## \[1\] "Correct Exceedances"
## \[1\] "Fail to Reject H0"
## \[1\] "Correct Exceedances & Independent"
## \[1\] "Fail to Reject H0"基于拟合模型预测VaR
现在预测VaR。
模拟X_t的未来轨迹并计算相应的VaR
模拟序列,估计每个模拟路径的VaR(注意quantile()这里不能使用,因此我们必须手动构建VaR)并计算VaR _alpha的bootstrap置信区间。
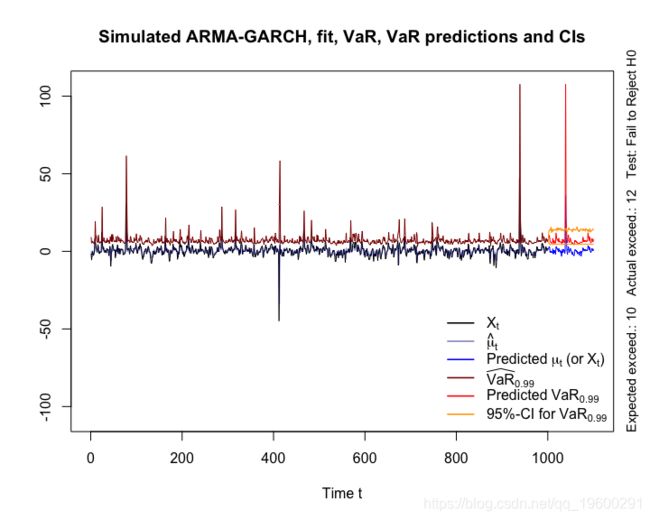
结果对比
最后,我们显示所有结果。
非常感谢您阅读本文,有任何问题请在下面留言!
最受欢迎的见解
1.R语言基于ARMA-GARCH-VaR模型拟合和预测实证研究