分解质因数 小O的质数 阶乘约数 求值 python

想说的话

大家好，我是 @愿此后再无WA，可以叫我小A，也可以叫我愿愿，一位阳光帅小伙，对算法领域比较感兴趣。如果我的文章对您有用，欢迎持续关注，我们一起进步！

很抱歉各位，现离蓝桥杯比赛不到一个月时间，我临时改变了计划，转为全心备战蓝桥，因为这个省一对我来说太重要了，也是我最后一次机会，我一定要拿到手，那么这样的话我在博客上花的时间就会少了很多，也将导致博客文章质量明显下降，在此我给大家说声抱歉

---

这些日子我真的很开心，博客上能遇到一群志同道合的兄弟姐妹真的很幸福，没有你们的支持与鼓励我早就坚持不下去了，因为有你们我才能走的更远☀️☀️熬过这段时期我一定会回来的，爱你们❤️❤️

吐槽

数论真的高深莫测呀…幸亏早些遇到，考试才遇到的话直接完蛋。幸好我好兄弟杨枝哥出了一片文章，看完之后学了不少，可惜是c++的，看的还是有点不太舒服吧。想看的朋友可以点这里.

分解质因数

题目描述

求出区间[a,b]中所有整数的质因数分解。

输入

输入两个整数a，b。
2< =a< =b< =10000

输出

3=3
4=2*2
5=5
6=2*3
7=7
8=2*2*2
9=3*3
10=2*5

分析

问题输出有点难受，但怎么说也是蓝桥vip试题，将就一下吧。

什么是质因数？

质因子（或质因数）在数论里是指能整除给定正整数的质数。根据算术基本定理，不考虑排列顺序的情况下，每个正整数都能够以唯一的方式表示成它的质因数的乘积。两个没有共同质因子的正整数称为互质。

因此，一个数如果没有其他质因数的话那么就是他的质因数就是他本身。

既然一个数可以由一个或若干个质因数表示出来，那么我们就能从小到大遍历这个数，如果遇到一个质因数，就不断对他作除，直到除不尽（直到有小数）才停下。等除完后这个数跟刚才的质因数已经没有任何关系了，接着就是找下一个质因数，重复上面步骤，直到这个数除到只剩下1为止。而前面分离出来的就是质因数了。打个比方，客厅桌上有块大饼，小明肚子饿了被他吃掉一口，再吃掉一口，等小明吃不下后他才进房间。这时候大饼已经少了一部分，小明也吃饱了，所以小明就不会再吃了，接着小明他爸看到了，因为肚子饿了也吃饼，当他吃饱后，如果还有的话他妈妈可能还会来吃等等。

现在我们就是要找出这些质因数，然后将其数量记录下来，最后输出。

代码

def divide(n):
    i = 2
    
    while n != 1:       
        if n % i == 0:
            s = 0   
                   
            while n != 1 and n % i == 0:              
                s += 1
                n /= i
                
            dic[i] = s
            
        i += 1

n,m = map(int,input().split())

for r in range(n,m+1):
    
    dic = {}
    divide(r)
    res = ""
    print(f'{r}=',end='')
    for i in dic:
        
        for j in range(dic[i]):

            res += f"{i}*"
    print(res[:-1])

小O的质数

思路

找质数可以使用埃氏筛法，每找出一个质数，就遍历一次数组，将质数倍数去掉，不断重复此步骤，之后就能得出质数的个数了。借用杨枝的一张图。

代码

def is_prime(n):
    if n == 2:
        return True

    if n % 2 == 0:
        return False
    
    for i in range(3,int(n**0.5)+1,2):
        if n % i == 0:
            return False
        
    return True

for _ in range(6):
    n, m = map(int,input().split())
    nums = [i for i in range(n,m+1)]
    result = 0

    for i in range(m-n+1):

        if nums[i]:
            result += 1

            for j in range(i,m-n+1,nums[i]):
                nums[j] = 0
                
                # print(nums)
    print(result)

阶乘约数

题目

分析

咳咳，这是国赛题，我们首先要了解正约数怎么求，咱们又来看看杨枝小可爱整理的那篇文章，非常good。



一定要搞懂求约数个数与求约数和，剩下的就简单了。

我们就是遍历1到100，将所有质因数个数记录起来，最后使用上面的公式输出。

代码

def prime_factor(n):
    
    i = 2
    
    while n != 1:        
        if n % i == 0:            
            s = 0           
            while n != 1 and n % i == 0:
                
                n /= i
                s += 1           
                 
            if i in dic:
                dic[i] += s
            else:
                dic[i] = s
                
        i += 1

dic = {}

for i in range(1,101):
    prime_factor(i)
    
res = 1

for i in dic.values():
    res *= i+1
print(res)

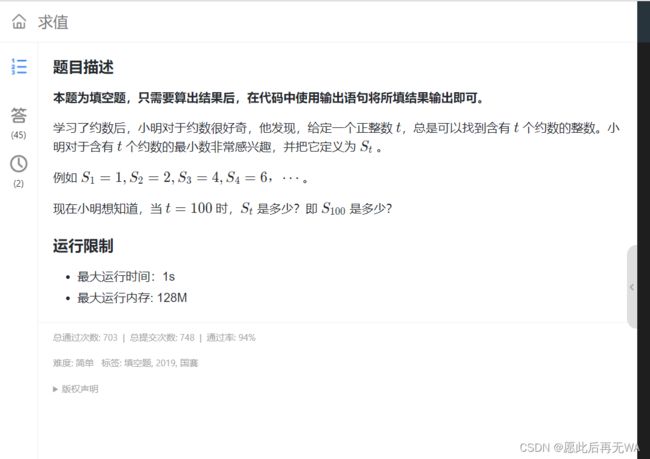
求值

分析

这是国赛题，如果如果清楚了正约数可以通过质因数来求，而又知道质因数个数怎么求的话这题就变得比较简单了，就是遍历所有数字得出它们所有的质因数及个数，最后套用公式求解，如果是100则返回结果。不太清晰的同学可以再看一下这张图

代码

def prime(n):
    
    mem = {}
    
    for i in range(2,n+1):
        
        if n % i == 0:

            cnt = 0
            while n != 1 and n % i == 0:
                n //= i
                cnt += 1
                
            mem[i] = cnt

            if n == 1:
                res = 1
                for i in mem:
                    res *= mem[i]+1
                return res

for i in range(4,int(1e6)):
    if prime(i) == 100:
        print(i)
        break