注意力机制
注意力机制
之前接触到的seq2seq模型当中,解码器只依赖编码器最后一个时间步的隐藏状态作为解码器自身的初始隐藏状态。这个隐藏状态融合了所有输入序列的信息。
注意力机制的提出与一个心理学问题相关,假如我们需要观察一个人是否在睡觉,输入我们大脑的是从我们视觉神经获取的一个人的图像。我们为了判断此人是否在睡觉,我们会习惯地去看他的眼睛是不是闭着的,也就是说,我们将更多的注意力集中在观察对方的眼睛上而不是对方的耳朵或是鼻子。
第一段中提到的融合了所有输入序列的信息,就像是上段中提到的包含此人所有特征的图像。我们是否可以把注意力集中到某一个特定部分从而提高模型的效率。注意力机制由此提出。
所谓注意力机制,就是通过引入一个神经网络,计算编码器在各个时间步的隐藏状态对解码器贡献的权重,最后计算加权后编码器的输出,及上下文(Context)。通过在解码器更新隐藏状态的过程中引入上下文信息,最后达到让解码器德某一个特定解码和编码器的一些隐藏状态关联起来的效果。通俗来讲,可以理解为让解码器的某一个特定解码“格外注意”编码器中的某些隐藏状态。
具体来讲,以机器翻译为例。要将“I love China”翻译成中文“我爱中国”,在准备翻译出“我”这个字的时候,输入序列中的“I”是与之最相关的,我们要将注意力集中在“I”上。可见,注意力机制的核心在于对给定信息进行权重分配,权重高的信息意味着需要系统进行重点加工。注意力机制是怎样做到这个的?它是通过判断当前时间步解码器的隐藏状态与各个时间步编码器的隐藏状态的相似度分数来生成注意力权重,达到分配注意力的效果。
注意力机制的定义如下:
A t t e n t i o n ( Q u e r y , S o u r c e ) = ∑ i s c o r e ( Q u e r y , K e y i ) ⋅ V a l u e i Attention(Query,Source) = \sum_{i}score(Query,Key_i) \cdot Value_i Attention(Query,Source)=i∑score(Query,Keyi)⋅Valuei
其中,Source是需要系统处理的信息源,Query表示某种条件或者先验信息,Attention(Query,Source) 是给定Query的条件下,通过注意力机制从Source中提取得到的信息。;一般Source中的信息通过Key-Value对的形式表达出来。
拿融入注意力机制的seq2seq模型举例,假设时间步 t t t 时编码器的隐藏状态为 h t h_t ht ,时间步 t ′ t' t′ 时解码器的隐藏状态为 s t ′ s_{t'} st′。我们很自然地将Query设置为解码器当前的隐藏状态,将Source设置为所有编码器的隐藏状态。不过其中 K e y = V a l u e = h t Key=Value=h_t Key=Value=ht,有两种典型的分数计算方法:
s c o r e ( s t ′ , h t ) = { v T t a n h ( W [ s t ′ ; h t ] + b ) [ B a h d a n a u ′ s A d d i t i v e A t t e n t i o n ] s t ′ T W h t [ l u o n g ′ s M u l t i p l i c a t i v e A t t e n t i o n ] score(s_{t'},h_t) = \begin{cases} v^Ttanh(W[s_{t'};h_t]+b)&[Bahdanau's\ Additive\ Attention]\\ s_{t'}^TWh_t &[luong's \ Multiplicative\ Attention] \end{cases} score(st′,ht)={vTtanh(W[st′;ht]+b)st′TWht[Bahdanau′s Additive Attention][luong′s Multiplicative Attention]
计算出当前解码时刻与各个编码时刻对应的相似度分数后,再根据该分数计算每个编码状态的注意力权重:
w t ′ t = e x p ( s c o r e ( s t ′ , h t ) ) ∑ k = 1 T s c o r e ( s t ′ , h k ) w_{t't} = \frac{exp(score(s_{t'},h_t))}{\sum_{k=1}^T score(s_{t'},h_k)} wt′t=∑k=1Tscore(st′,hk)exp(score(st′,ht))
w t ′ t w_{t't} wt′t 表示编码时刻 t t t 对解码时刻 t ′ t' t′ 的注意力权重,之后对编码器的隐藏状态做加权求和就得到了解码时刻 t ′ t' t′上下文。假设编码器总的时间步为T:
c t ′ = ∑ t = 1 T w t ′ t h t c_{t'} = \sum^{T}_{t=1}w_{t't}h_t ct′=t=1∑Twt′tht
得到了上下文,我们可以此来更新解码器 t ′ + 1 t'+1 t′+1 时的隐藏状态。其中 y t ′ y_{t'} yt′ 为 t ′ t' t′时解码器的输出。
s t ′ + 1 = f ( s t ′ , c t ′ , y t ′ ) s_{t'+1} = f(s_{t'},c_{t'},y_{t'}) st′+1=f(st′,ct′,yt′)
GAT
最近看了篇论文跟图注意力网络GAT(Graph Attention Networks)有关,这里做一下总结。对比之前的seq2seq模型,此时Query为当前中心节点的特征向量,将Source设置为所有邻居结点的特征向量,Attention(Query,Source)即为中心节点经过聚合操作后的新的特征向量。
设图中任意节点 v i v_i vi 在第l层的特征向量为 h i ∈ R d ( l ) h_i \in {R}^{d^{(l)}} hi∈Rd(l),经过一个以注意力机制为核心的聚合操作之后,输出的是每个结点新的特征向量 h i ′ ∈ R d ( l + 1 ) h_i' \in R^{d^{(l+1)}} hi′∈Rd(l+1)。将这个聚合操作称作图注意力层(Graph Attention Layer)
假设当前中心节点为 v i v_i vi, 该节点与节点 v j v_j vj 的相似度分数定义为:
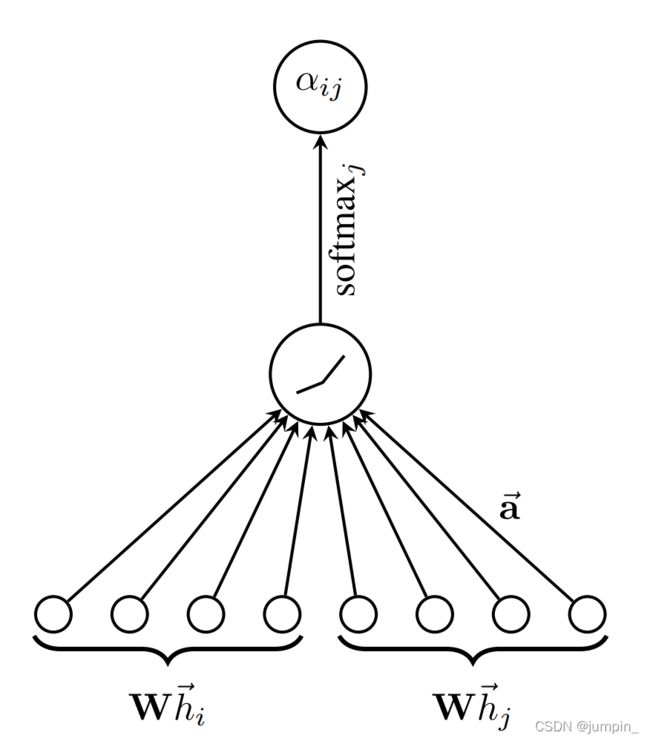
e i j = s c o r e ( W h i , W h j ) = L e a k l y R e l u ( a T [ W h i ∣ ∣ W h j ] ) \begin{aligned} e_{ij} &= score(Wh_i,Wh_j)\\ &= Leakly\ Relu(a^T[Wh_i||Wh_j]) \end{aligned} eij=score(Whi,Whj)=Leakly Relu(aT[Whi∣∣Whj])
其中 ∣ ∣ || ∣∣ 表示拼接操作, W ∈ R d ( l + 1 ) × d ( l ) W \in R^{d^{(l+1)}\times d^{(l)}} W∈Rd(l+1)×d(l) 是该层节点变换的权重参数, s c o r e score score 也可以选择内积进行相似度的计算,只要满足输出 e i j e_{ij} eij 是一个标量值即可,这里使用了一个单层的全连接层,其中 a ∈ R 2 d ( l + 1 ) a\in R^{2d^{(l+1)}} a∈R2d(l+1)为权重参数。
需要注意的是,我们可以计算出图中任意一个节点到节点 v i v_i vi 的相似度分数,但是为了简化计算,我们将其限制在一阶邻居内。在GAT中,作者将每个节点自身也视作自己的邻居。
之后则将所有一阶邻居的相似度用softmax进行归一化处理得到注意力权重:
α i j = s o f t m a x j e i j = e x p ( e i j ) ∑ v k ∈ N ( v i ) e x p ( e i k ) \alpha_{ij} = softmax_j{e_{ij} = \frac{exp(e_{ij})}{\sum_{v_k \in N(v_i)}exp(e_{ik})}} αij=softmaxjeij=∑vk∈N(vi)exp(eik)exp(eij)
完成上述注意力权重的计算之后,按照注意力机制加权求和即可得出节点 v i v_i vi 新的特征向量为:
h i ′ = σ ( ∑ v j ∈ N ( v i ) α i j W h j ) h_i' = \sigma(\sum_{v_j \in N(v_i)} \alpha_{ij}Wh_j) hi′=σ(vj∈N(vi)∑αijWhj)
多头图注意力
多头注意力机制可以进一步提升模型的表达能力,具体操作为对上式调用K组相互独立的注意力机制,然后将结果拼接在一起:
h i ′ = ∥ k = 1 K σ ( ∑ j ∈ N i α i j k W k h j ) {h}_{i}^{\prime}=\|_{k=1}^{K} \sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} {h}_{j}\right) hi′=∥k=1Kσ⎝⎛j∈Ni∑αijkWkhj⎠⎞
其中k表示第k组注意力机制。增加了多组相互独立的注意力机制,使得多头注意力机制能够将注意力的分配放到中心节点与邻居节点多处相关的特征上。
相比于GCN里面的图卷积操作,多头图注意力多了一个自适应的边权重系数的维度。
参考文献
[1] Velikovi, P.; Cucurull, G.; Casanova, A.; Romero, A.; Li, P.; and Bengio, Y. 2018. Graph attention networks. In ICLR.
[2] Sutskever, I., Vinyals, O., & Le, Q. V. (2014). Sequence to sequence learning with neural networks. In Advances in neural information processing systems (pp. 3104-3112).
[3] Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.