详解反向传播神经网络 （Back Propagation Neural Network, BPNN）

一、基本概念

所谓神经网络，本质上也是用训练样本构造出一个回归模型，与经典回归模型所不同的是它的函数形式并不简洁，而是多重函数的嵌套，因此它无法给出数据之间关系的直观描述，而给人一种黑盒的感觉。但其价值在于，理论上可以拟合多输入多输出的任意非线性函数，故而在回归、聚类等多领域都可应用。而神经网络中又以反向传播神经网络最为经典，此文将给出此类神经网络的基本原理和使用方法。

（一）单一神经元数学模型

根据生物神经元细胞的构造抽象出单一神经元数学模型，如图1所示：

图1 单一神经元模型

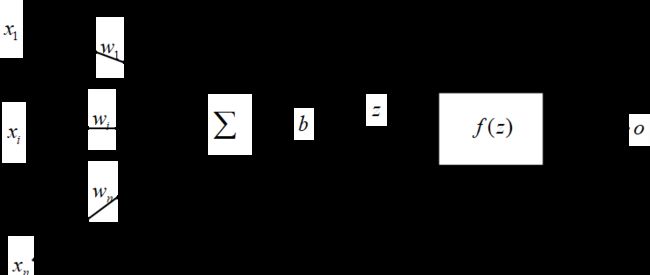
多个外界输入（$x_1\sim x_n$）经分别加权后求和，并做一定偏移（$b$），输入到一个非线性激励函数（$f$）中，最后得到该神经元的输出值（$o$）。其数学表达式为：
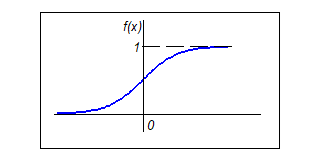
$$o=f\left(\sum _{i=1}^n{w}_i{x}_i+b\right)=f({\mathbf{w}}^T\mathbf{x}+b)$$由于进入到每个神经元各外部输入都是经过一个线性组合，即组成一个线性函数后再作为自变量进入到该神经元的的激励函数，如果激励也是一个线性函数，那就成了线性函数的线性函数，最终还是线性函数，如此一来，无论多少个神经元组成的神经网络也只能化归成一个线性函数。因此激励函数必须是非线性的，才能通过多层神经元组合连接，加权嵌套出任意非线性函数，实现复杂问题处理。激励函数一般选用以下三种类型：

名称	特征	表达式	图像
Sigmoid函数	正值，可微，类阶跃	$f(x)=\frac{1}{1+e^{-x}}$
双曲正切函数	零均值，可微，类阶跃	$f(x)=\tanh (x)$
高斯函数	正值，可微，类脉冲	$f(x)=\exp (-\frac{x^2}{{\sigma }^2})$

由各激励函数图像可见，只在0附近会产生显著的响应差异，所以要在激励函数的输入中引入偏移量（$b$），从而相当于对响应函数做了适当平移。

（二）多层BPNN的定义

当多个神经元形成多层交叉连接时，即形成神经网络。前一层神经元的输出成为后一层神经元的输入，最后一层直接给出整个网络输出的神经元称为输出层，输出层前面的各层称为隐含层。当一个神经网络有一个以上的隐含层时，称为深度学习网络。此文以一个含有两个隐含层（共三层神经元）的深度学习网络为例做阐述，其构造如图2所示，其运算和训练过程可推广至更多层网络。

图2 深度学习网络

该网络的入参是一个$n$维向量$\mathbf{x}=\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right]$，出参是一个$m$维向量$\mathbf{y}=\left[\begin{array}{cccc}{y}_1& y_2& \cdots & y_m\end{array}\right]$。从左至右，各层神经元的输入权重矩阵、偏移向量、入参向量、出参向量分别是：
$${\mathbf{w}}^{(1)}=\left[\begin{array}{cccc}{w}_{11}^{(1)}& w_{21}^{(1)}& \cdots & w_{n1}^{(1)}\\ w_{12}^{(1)}& w_{22}^{(1)}& \cdots & w_{n2}^{(1)}\\ ⋮& ⋮& \ddots & ⋮\\ w_{1k}^{(1)}& w_{2k}^{(1)}& \cdots & w_{nk}^{(1)}\end{array}\right]{\mathbf{b}}^{(1)}=\left[\begin{array}{c}{b}_1^{(1)}\\ b_2^{(1)}\\ ⋮\\ b_k^{(1)}\end{array}\right]{\mathbf{z}}^{(1)}=\left[\begin{array}{c}{z}_1^{(1)}\\ z_2^{(1)}\\ ⋮\\ z_k^{(1)}\end{array}\right]{\mathbf{o}}^{(1)}=\left[\begin{array}{c}{o}_1^{(1)}\\ o_2^{(1)}\\ ⋮\\ o_k^{(1)}\end{array}\right]$$$${\mathbf{w}}^{(2)}=\left[\begin{array}{cccc}{w}_{11}^{(2)}& w_{21}^{(2)}& \cdots & w_{k1}^{(2)}\\ w_{12}^{(2)}& w_{22}^{(2)}& \cdots & w_{k2}^{(2)}\\ ⋮& ⋮& \ddots & ⋮\\ w_{1k}^{(2)}& w_{2k}^{(2)}& \cdots & w_{kl}^{(2)}\end{array}\right]{\mathbf{b}}^{(2)}=\left[\begin{array}{c}{b}_1^{(2)}\\ b_2^{(2)}\\ ⋮\\ b_l^{(2)}\end{array}\right]{\mathbf{z}}^{(2)}=\left[\begin{array}{c}{z}_1^{(2)}\\ z_2^{(2)}\\ ⋮\\ z_l^{(2)}\end{array}\right]{\mathbf{o}}^{(2)}=\left[\begin{array}{c}{o}_1^{(2)}\\ o_2^{(2)}\\ ⋮\\ o_l^{(2)}\end{array}\right]$$$${\mathbf{w}}^{(3)}=\left[\begin{array}{cccc}{w}_{11}^{(3)}& w_{21}^{(3)}& \cdots & w_{l1}^{(3)}\\ w_{12}^{(3)}& w_{22}^{(3)}& \cdots & w_{l2}^{(3)}\\ ⋮& ⋮& \ddots & ⋮\\ w_{1k}^{(3)}& w_{2k}^{(3)}& \cdots & w_{lm}^{(3)}\end{array}\right]{\mathbf{b}}^{(3)}=\left[\begin{array}{c}{b}_1^{(3)}\\ b_2^{(3)}\\ ⋮\\ b_m^{(3)}\end{array}\right]{\mathbf{z}}^{(3)}=\left[\begin{array}{c}{z}_1^{(3)}\\ z_2^{(3)}\\ ⋮\\ z_m^{(3)}\end{array}\right]{\mathbf{o}}^{(3)}=\left[\begin{array}{c}{o}_1^{(3)}\\ o_2^{(3)}\\ ⋮\\ o_m^{(3)}\end{array}\right]$$其中$w_{jk}^{(i)}$表示第$i$层神经元前第$j$个输入源传达该层第$k$个神经元上的强度权重；$b_j^{(i)}$表示第$i$层第$j$个神经元的输入偏移量；$z_j^{(i)}$表示第$i$层第$j$个神经元的激励函数入参；$o_j^{(i)}$表示第$i$层第$j$个神经元的激励函数出参。最后一层神经元的出参也就是整个神经网络的输出向量，即${\mathbf{o}}^{(3)}=\hat{\mathbf{y}}=\left[\begin{array}{cccc}{\hat{y}}_1& {\hat{y}}_2& \cdots & {\hat{y}}_m\end{array}\right]$。第一层神经元的输入源即为整个神经网络的输入向量，即$\mathbf{x}=\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right]$。

二、运算过程

基于上述定义，该神经网络的运算过程可表示为：
$${\mathbf{z}}^{(1)}={\mathbf{w}}^{(1)}\otimes \mathbf{x}+{\mathbf{b}}^{(1)},{\mathbf{o}}^{(1)}=f({\mathbf{z}}^{(1)})$$$${\mathbf{z}}^{(2)}={\mathbf{w}}^{(2)}\otimes {\mathbf{o}}^{(1)}+{\mathbf{b}}^{(2)},{\mathbf{o}}^{(2)}=f({\mathbf{z}}^{(2)})$$$${\mathbf{z}}^{(3)}={\mathbf{w}}^{(3)}\otimes {\mathbf{o}}^{(2)}+{\mathbf{b}}^{(3)},{\mathbf{o}}^{(3)}=f({\mathbf{z}}^{(3)})$$对于其中运算符$“\otimes ”$，当将其定义为做内积时，就是普通BP网络；当将其定义为右边向量与左边矩阵各行向量求欧氏距时，就成了径向基网络（Radial Basis Funtion, RBF），一种有监督聚类网络，此时如果神经元的激励函数是高斯函数，则相当于其权重向量越是离输入向量距离近的神经元越会被激活。

三、训练过程

目前看来，神经网络运算的原理并不复杂，在实际应用中也确实不会对运算资源带来多大消耗。非常消耗计算资源的是网络的训练过程，其原理也相对复杂，需要使得其可以每次训练中找到不足的原因，并做出改进，直到可以对每个输入都能给出完美输出。本章将阐述如何定量输出与预想结果的不足，如何迭代改进各神经元的权重和偏移量使得神经网络最终输出预想结果。

（一）代价函数

此处定义代价函数为一个训练样本集中各样本训练误差的均值，用来定量描述每组训练中神经网络表现不佳的程度。设一个样本量为$t$的训练样本集合，其入参向量集为$\{{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_t\}$，其中每个入参是一个$n$维向量；对应的出参向量集为$\{{\mathbf{y}}_1,{\mathbf{y}}_2,\cdots ,{\mathbf{y}}_t\}$，其中每个出参是一个$m$维向量。则代价函数为：
$$J({\mathbf{w}}^{(1)},{\mathbf{w}}^{(2)},{\mathbf{w}}^{(3)},{\mathbf{b}}^{(1)},{\mathbf{b}}^{(2)},{\mathbf{b}}^{(3)})=\frac{1}{t}\sum _{i=1}^t{L}_i$$其中$L_i$表示第$i$个训练样本的训练误差，为方便后续计算，将其定义为该样本出参向量与预测向量欧氏距平方的一半，即
$$L_i({\mathbf{w}}^{(1)},{\mathbf{w}}^{(2)},{\mathbf{w}}^{(3)},{\mathbf{b}}^{(1)},{\mathbf{b}}^{(2)},{\mathbf{b}}^{(3)})=\frac{1}{2}\Vert {\mathbf{y}}_i-{\hat{\mathbf{y}}}_i{\Vert }^2=\frac{1}{2}\sum _{j=1}^m(y_{ij}-{\hat{y}}_{ij}{)}^2$$由于代价函数就是一个由各层神经元各权重和各偏移量构成的多元函数，训练神经网络的目的在于找到一组使得该代价函数取得最小值的各层神经元权重矩阵和偏移向量。这里要引入梯度下降法。梯度就是由多元函数各自变量的偏导数组成的向量，一个自变量的偏导数反应了该自变量对函数值增长的影响度，所以一个多元函数的梯度指向的就是在多维空间中该函数值增长最快的方向，而反方向就是函数值下降最快的方向，沿此方向移动自变量，即所谓梯度下降。根据每次迭代训练计算代价函数梯度时所选用的训练样本集合不同，分为三种梯度下降方式：

1. 批量梯度下降（Batch Gradient Descent，BGD）。即每次训练迭代时，使用当前训练样本集合的全集来计算代价函数梯度。
2. 随机梯度下降（Stochastic Gradient Descent，SGD）。即每次训练迭代时，仅使用当前训练样本集合中的一个随机样本来计算代价函数梯度。
3. 小批量梯度下降（Mini-Batch Gradient Descent, MBGD）。即每次训练迭代时，使用当前训练样本集合中的一个随机子集样本来计算代价函数梯度。此训练方案是上述两种方案的折中，一般效果最好。

（二）梯度推导

由上述看来，训练神经网络的关键是先求得其代价函数的梯度，才能沿梯度下降方向一步步优化网络参数。由于和的导数就等于导数的和，即
$$\frac{d}{dx}[f_1(x)+f_2(x)]=\frac{d}{dx}{f}_1(x)+\frac{d}{dx}{f}_2(x)$$由于梯度是各偏导数组成的向量，因此同样适用上述性质，因而
$$\nabla J=\frac{1}{t}\sum _{i=1}^t\nabla L_i$$对于其中任一个训练样本，其误差函数的梯度为：
$$\nabla L=\left\{\begin{array}{cccccc}\frac{\partial L}{\partial {\mathbf{w}}^{(1)}}& \frac{\partial L}{\partial {\mathbf{w}}^{(2)}}& \frac{\partial L}{\partial {\mathbf{w}}^{(3)}}& \frac{\partial L}{\partial {\mathbf{b}}^{(1)}}& \frac{\partial L}{\partial {\mathbf{b}}^{(2)}}& \frac{\partial L}{\partial {\mathbf{b}}^{(3)}}\end{array}\right\}$$上式之所以用大括号是因为其中每个元素又是一个矩阵或向量。首先考虑各权重矩阵的偏导。以第一层神经元为例，由前述神经网络运算过程可知，$w_{1q}^{(1)}\sim w_{nq}^{(1)}$都仅是$z_q^{(1)}$的自变量，而$z_q^{(1)}$又是$L$的自变量。对于嵌套函数$f[g(x)]$，其导数为
$$\frac{df}{dx}=\frac{df}{dg}\frac{dg}{dx}$$换成偏导数同样适用此法则，因此
$$\frac{\partial L}{\partial w_{pq}^{(1)}}=\frac{\partial L}{\partial z_q^{(1)}}\frac{\partial z_q^{(1)}}{\partial w_{pq}^{(1)}}$$以此类推有
$$\frac{\partial L}{\partial {\mathbf{w}}^{(1)}}=\left[\begin{array}{cccc}\frac{\partial L}{\partial w_{11}^{(1)}}& \frac{\partial L}{\partial w_{21}^{(1)}}& \cdots & \frac{\partial L}{\partial w_{n1}^{(1)}}\\ \frac{\partial L}{\partial w_{12}^{(1)}}& \frac{\partial L}{\partial w_{22}^{(1)}}& \cdots & \frac{\partial L}{\partial w_{n2}^{(1)}}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{\partial L}{\partial w_{1k}^{(1)}}& \frac{\partial L}{\partial w_{2k}^{(1)}}& \cdots & \frac{\partial L}{\partial w_{nk}^{(1)}}\end{array}\right]=\left[\begin{array}{cccc}\frac{\partial L}{\partial z_1^{(1)}}\frac{\partial z_1^{(1)}}{\partial w_{11}^{(1)}}& \frac{\partial L}{\partial z_1^{(1)}}\frac{\partial z_1^{(1)}}{\partial w_{21}^{(1)}}& \cdots & \frac{\partial L}{\partial z_1^{(1)}}\frac{\partial z_1^{(1)}}{\partial w_{n1}^{(1)}}\\ \frac{\partial L}{\partial z_2^{(1)}}\frac{\partial z_2^{(1)}}{\partial w_{12}^{(1)}}& \frac{\partial L}{\partial z_2^{(1)}}\frac{\partial z_2^{(1)}}{\partial w_{22}^{(1)}}& \cdots & \frac{\partial L}{\partial z_2^{(1)}}\frac{\partial z_2^{(1)}}{\partial w_{n2}^{(1)}}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{\partial L}{\partial z_k^{(1)}}\frac{\partial z_k^{(1)}}{\partial w_{1k}^{(1)}}& \frac{\partial L}{\partial z_k^{(1)}}\frac{\partial z_k^{(1)}}{\partial w_{2k}^{(1)}}& \cdots & \frac{\partial L}{\partial z_k^{(1)}}\frac{\partial z_k^{(1)}}{\partial w_{nk}^{(1)}}\end{array}\right]$$由前述神经网络运算过程可知，其中
$$\frac{\partial z_1^{(1)}}{\partial w_{p1}^{(1)}}=\frac{\partial z_2^{(1)}}{\partial w_{p2}^{(1)}}=\cdots =\frac{\partial z_k^{(1)}}{\partial w_{pk}^{(1)}}=x_p$$所以
$$\frac{\partial L}{\partial {\mathbf{w}}^{(1)}}=\left[\begin{array}{c}\frac{\partial L}{\partial z_1^{(1)}}\\ \frac{\partial L}{\partial z_2^{(1)}}\\ ⋮\\ \frac{\partial L}{\partial z_k^{(1)}}\end{array}\right]\left[\begin{array}{cccc}\frac{\partial z_q^{(1)}}{\partial w_{1q}^{(1)}}& \frac{\partial z_q^{(1)}}{\partial w_{2q}^{(1)}}& \cdots & \frac{\partial z_q^{(1)}}{\partial w_{nq}^{(1)}}\end{array}\right]=\left[\begin{array}{c}\frac{\partial L}{\partial z_1^{(1)}}\\ \frac{\partial L}{\partial z_2^{(1)}}\\ ⋮\\ \frac{\partial L}{\partial z_k^{(1)}}\end{array}\right]\left[\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right]={\mathbf{\delta }}^{(1)}{\mathbf{x}}^T$$同理可得
$$\frac{\partial L}{\partial {\mathbf{w}}^{(2)}}={\mathbf{\delta }}^{(2)}({\mathbf{o}}^{(1)}{)}^T$$$$\frac{\partial L}{\partial {\mathbf{w}}^{(3)}}={\mathbf{\delta }}^{(3)}({\mathbf{o}}^{(2)}{)}^T$$再考虑各偏移向量的偏导数。以第一层神经元为例，由前述神经网络运算过程可知，$b_q^{(1)}$仅是$z_q^{(1)}$的自变量，所以有
$$\frac{\partial L}{\partial b_q^{(1)}}=\frac{\partial L}{\partial z_q^{(1)}}\frac{\partial z_q^{(1)}}{\partial b_q^{(1)}}=\frac{\partial L}{\partial z_q^{(1)}}$$因为其中$\frac{\partial z_q^{(1)}}{\partial b_q^{(1)}}=1$。以此类推有
$$\frac{\partial L}{\partial {\mathbf{b}}^{(1)}}=\left[\begin{array}{c}\frac{\partial L}{\partial b_1^{(1)}}\\ \frac{\partial L}{\partial b_2^{(1)}}\\ ⋮\\ \frac{\partial L}{\partial b_k^{(1)}}\end{array}\right]=\left[\begin{array}{c}\frac{\partial L}{\partial z_1^{(1)}}\\ \frac{\partial L}{\partial z_2^{(1)}}\\ ⋮\\ \frac{\partial L}{\partial z_k^{(1)}}\end{array}\right]={\mathbf{\delta }}^{(1)}$$同理可得
$$\frac{\partial L}{\partial {\mathbf{b}}^{(2)}}={\mathbf{\delta }}^{(2)}$$$$\frac{\partial L}{\partial {\mathbf{b}}^{(3)}}={\mathbf{\delta }}^{(3)}$$综上所述，任一组训练样本的误差函数梯度为：
$$\nabla L=\left\{\begin{array}{cccccc}{\mathbf{\delta }}^{(1)}{\mathbf{x}}^T& {\mathbf{\delta }}^{(2)}({\mathbf{o}}^{(1)}{)}^T& {\mathbf{\delta }}^{(3)}({\mathbf{o}}^{(2)}{)}^T& {\mathbf{\delta }}^{(1)}& {\mathbf{\delta }}^{(2)}& {\mathbf{\delta }}^{(3)}\end{array}\right\}$$此时可以发现计算梯度的关键是计算出${\mathbf{\delta }}^{(i)}$，它被称为第$i$层神经元的灵敏度，反映了第$i$层神经元对网络总输出误差的影响程度。仍以第一层神经元为例，由于$z_1^{(1)}$仅是一个激励函数的入参，即仅是$o_1^{(1)}$的自变量，而$o_1^{(1)}$是下一层所有神经元激励函数入参${\mathbf{z}}^{(2)}$的自变量。对于一个多元嵌套函数，其偏导计算公式为：
$$\frac{\partial }{\partial x_1}f[g_1(x_1,x_2),g_2(x_1,x_2)]=\frac{\partial f}{\partial g_1}\frac{\partial g_1}{\partial x_1}+\frac{\partial f}{\partial g_2}\frac{\partial g_2}{\partial x_1}$$所以有
$$\frac{\partial L}{\partial z_1^{(1)}}=\frac{\partial L}{\partial o_1^{(1)}}\frac{\partial o_1^{(1)}}{\partial z_1^{(1)}}=\frac{\partial L}{\partial o_1^{(1)}}{f}^{\prime }(z_1^{(1)})=f^{\prime }(z_1^{(1)})\left[\frac{\partial L}{\partial z_1^{(2)}}\frac{\partial z_1^{(2)}}{\partial o_1^{(1)}}+\frac{\partial L}{\partial z_2^{(2)}}\frac{\partial z_2^{(2)}}{\partial o_1^{(1)}}+\cdots +\frac{\partial L}{\partial z_l^{(2)}}\frac{\partial z_l^{(2)}}{\partial o_1^{(1)}}\right]$$以此类推
$${\mathbf{\delta }}^{(1)}=\frac{\partial L}{\partial {\mathbf{z}}^{(1)}}=\left[\begin{array}{c}\frac{\partial L}{\partial z_1^{(1)}}\\ \frac{\partial L}{\partial z_2^{(1)}}\\ ⋮\\ \frac{\partial L}{\partial z_k^{(1)}}\end{array}\right]=\left[\begin{array}{cccc}{f}^{\prime }(z_1^{(1)})& & & \\ & f^{\prime }(z_2^{(1)})& & \\ & & \ddots & \\ & & & f^{\prime }(z_k^{(1)})\end{array}\right]\left[\begin{array}{cccc}\frac{\partial z_1^{(2)}}{\partial o_1^{(1)}}& \frac{\partial z_2^{(2)}}{\partial o_1^{(1)}}& \cdots & \frac{\partial z_l^{(2)}}{\partial o_1^{(1)}}\\ \frac{\partial z_1^{(2)}}{\partial o_2^{(1)}}& \frac{\partial z_2^{(2)}}{\partial o_2^{(1)}}& \cdots & \frac{\partial z_l^{(2)}}{\partial o_2^{(1)}}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{\partial z_1^{(2)}}{\partial o_k^{(1)}}& \frac{\partial z_2^{(2)}}{\partial o_k^{(1)}}& \cdots & \frac{\partial z_l^{(2)}}{\partial o_k^{(1)}}\end{array}\right]\left[\begin{array}{c}\frac{\partial L}{\partial z_1^{(2)}}\\ \frac{\partial L}{\partial z_2^{(2)}}\\ ⋮\\ \frac{\partial L}{\partial z_l^{(2)}}\end{array}\right]$$即
$${\mathbf{\delta }}^{(1)}=\frac{\partial {\mathbf{o}}^{(1)}}{\partial {\mathbf{z}}^{(1)}}\frac{\partial {\mathbf{z}}^{(2)}}{\partial {\mathbf{o}}^{(1)}}\frac{\partial \mathbf{L}}{\partial {\mathbf{z}}^{(2)}}=diag[f^{\prime }({\mathbf{z}}^{(1)})]({\mathbf{w}}^{(2)}{)}^T{\mathbf{\delta }}^{(2)}$$同理可得
$${\mathbf{\delta }}^{(2)}=\frac{\partial {\mathbf{o}}^{(2)}}{\partial {\mathbf{z}}^{(2)}}\frac{\partial {\mathbf{z}}^{(3)}}{\partial {\mathbf{o}}^{(2)}}\frac{\partial \mathbf{L}}{\partial {\mathbf{z}}^{(3)}}=diag[f^{\prime }({\mathbf{z}}^{(2)})]({\mathbf{w}}^{(3)}{)}^T{\mathbf{\delta }}^{(3)}$$可见每一层神经元的灵敏度都是前一层神经元灵敏度的自变量（即入参），这也就体现了误差从输出层反向传播到输入层，故而称这种网络为反向传播网络。正是因为这个特性，使得无论有多少层神经元，只要知道了最后一层输出层神经元的灵敏度，就可以很方便的迭代出各层神经元的灵敏度。在本文所举例的三层BPNN中，输出层的灵敏度为：
$${\mathbf{\delta }}^{(3)}=\frac{\partial \mathbf{L}}{\partial {\mathbf{z}}^{(3)}}=\left[\begin{array}{c}\frac{\partial L}{\partial z_1^{(3)}}\\ \frac{\partial L}{\partial z_2^{(3)}}\\ ⋮\\ \frac{\partial L}{\partial z_m^{(3)}}\end{array}\right]$$其中，由于$z_1^{(3)}$仅是$o_1^{(3)}$（即${\hat{y}}_1$）的自变量，而${\hat{y}}_1$又仅是误差函数$L$的自变量，所以有
$$\frac{\partial L}{\partial z_1^{(3)}}=\frac{\partial L}{\partial o_1^{(3)}}\frac{\partial o_1^{(3)}}{\partial z_1^{(3)}}=\frac{\partial L}{\partial {\hat{y}}_1}{f}^{\prime }(z_1^{(3)})=(y_1-{\hat{y}}_1)f^{\prime }(z_1^{(3)})$$以此类推
$${\mathbf{\delta }}^{(3)}=\frac{\partial \mathbf{L}}{\partial {\mathbf{z}}^{(3)}}=\left[\begin{array}{c}\frac{\partial L}{\partial z_1^{(3)}}\\ \frac{\partial L}{\partial z_2^{(3)}}\\ ⋮\\ \frac{\partial L}{\partial z_m^{(3)}}\end{array}\right]=\left[\begin{array}{cccc}{f}^{\prime }(z_1^{(3)})& & & \\ & f^{\prime }(z_2^{(3)})& & \\ & & \ddots & \\ & & & f^{\prime }(z_m^{(3)})\end{array}\right]\left[\begin{array}{c}{y}_1-{\hat{y}}_1\\ y_2-{\hat{y}}_2\\ ⋮\\ y_m-{\hat{y}}_m\end{array}\right]=diag[f^{\prime }({\mathbf{z}}^{(3)})](\mathbf{y}-\hat{\mathbf{y}})$$至此，误差函数的梯度公式可以进一步细化为
$$\nabla L=\left\{\begin{array}{c}\frac{\partial L}{\partial {\mathbf{w}}^{(1)}}\\ \frac{\partial L}{\partial {\mathbf{w}}^{(2)}}\\ \frac{\partial L}{\partial {\mathbf{w}}^{(3)}}\\ \frac{\partial L}{\partial {\mathbf{b}}^{(1)}}\\ \frac{\partial L}{\partial {\mathbf{b}}^{(2)}}\\ \frac{\partial L}{\partial {\mathbf{b}}^{(3)}}\end{array}\right\}=\left\{\begin{array}{c}{\mathbf{\delta }}^{(1)}{\mathbf{x}}^T\\ {\mathbf{\delta }}^{(2)}({\mathbf{o}}^{(1)}{)}^T\\ {\mathbf{\delta }}^{(3)}({\mathbf{o}}^{(2)}{)}^T\\ {\mathbf{\delta }}^{(1)}\\ {\mathbf{\delta }}^{(2)}\\ {\mathbf{\delta }}^{(3)}\end{array}\right\}=\left\{\begin{array}{c}diag[f^{\prime }({\mathbf{z}}^{(1)})]({\mathbf{w}}^{(2)}{)}^{T}diag[f^{\prime }({\mathbf{z}}^{(2)})]({\mathbf{w}}^{(3)}{)}^{T}diag[f^{\prime }({\mathbf{z}}^{(3)})](\mathbf{y}-\hat{\mathbf{y}}){\mathbf{x}}^T\\ diag[f^{\prime }({\mathbf{z}}^{(2)})]({\mathbf{w}}^{(3)}{)}^{T}diag[f^{\prime }({\mathbf{z}}^{(3)})](\mathbf{y}-\hat{\mathbf{y}})({\mathbf{o}}^{(1)}{)}^T\\ diag[f^{\prime }({\mathbf{z}}^{(3)})](\mathbf{y}-\hat{\mathbf{y}})({\mathbf{o}}^{(2)}{)}^T\\ diag[f^{\prime }({\mathbf{z}}^{(1)})]({\mathbf{w}}^{(2)}{)}^{T}diag[f^{\prime }({\mathbf{z}}^{(2)})]({\mathbf{w}}^{(3)}{)}^{T}diag[f^{\prime }({\mathbf{z}}^{(3)})](\mathbf{y}-\hat{\mathbf{y}})\\ diag[f^{\prime }({\mathbf{z}}^{(2)})]({\mathbf{w}}^{(3)}{)}^{T}diag[f^{\prime }({\mathbf{z}}^{(3)})](\mathbf{y}-\hat{\mathbf{y}})\\ diag[f^{\prime }({\mathbf{z}}^{(3)})](\mathbf{y}-\hat{\mathbf{y}})\end{array}\right\}$$设其中激活函数选用Sigmoid函数，即$f(x)=\frac{1}{1+e^{-x}}$，所以有
$$f^{\prime }(x)=(1+e^{-x}{)}^{-2}{e}^{-x}=f(x)[1-f(x)]$$故而
$$f^{\prime }({\mathbf{z}}^{(i)})=diag[f({\mathbf{z}}^{(i)})][1-f({\mathbf{z}}^{(i)})]=diag({\mathbf{o}}^{(i)})(1-{\mathbf{o}}^{(i)})$$至此，训练样本集合中的每个训练样本的误差函数梯度（$\nabla L$）都可以计算出来了，将其都代入前述代价函数梯度公式（即算数平均值）即得到代价函数梯度。

（三）迭代训练

由于梯度描述的是函数值增长最快的方向，因此为找到使代价函数取得最小值的点，则需沿梯度反方向前进，即向所谓梯度下降方向对所有权重和偏移量做一小步调整，此调整的大小称为迭代步长。然后再重新计算当前梯度，再做反向调整，周而复始直到梯度值足够小为止。

四、归一化

归一化是一个线性变化过程。即用向量的每一个值除以这些向量的一种共同线性范数（一般可取模长、最大坐标、或是最大与最小坐标间距等），还可再做一些相对平移使其中心化。即通过线性变换将每个量都统一成同一单位（或无量纲值，如占比），从而可以互相进行比较。这就如同要比较一个学生俩次成绩的好坏，不应该比较分数，而应该比较名次一样。
由各响应函数的图像可见，神经网络的各输出值范围只能是在$[0,1]$或$[-1,1]$之间，故而要用于处理实际问题时也必须对出参做归一化处理。对训练样本出参可做归一化处理如下：
$${\mathbf{y}}^{。}=\frac{\mathbf{y}-\min (\mathbf{y})}{\max (\mathbf{y})-\min (\mathbf{y})}$$其中$\mathbf{y}$为一个训练样本出参向量，${\mathbf{y}}^{。}$为归一化后的该训练样本出参向量。当已知待估计结果的值域后，如上限和下限向量分别为$\mathbf{m}$和$\mathbf{n}$，则对神经网络估计出的结果须做反归一化处理：
$$\hat{\mathbf{y}}={\hat{\mathbf{y}}}^{。}(\mathbf{m}-\mathbf{n})+\mathbf{n}$$其中${\hat{\mathbf{y}}}^{。}$为整个神经网络输出的估计向量，本身就是归一化的。

五、应用示例

此例中根据给定的平面直角坐标系上的一系列点来训练一个BPNN，从而拟合出一条曲线。使用python语言实现。

（一）数据准备

import numpy as np
import matplotlib.pyplot as plt

# 定义一个函数
def f(x):
    return np.sin(x) + 0.5*x

# 利用上述函数创建出一系列离散点，并绘制出图像
x = np.linspace(-2*np.pi, 2*np.pi, 50)
y = f(x)
plt.figure(2)
plt.plot(x, y, 'b.', label='points')
plt.legend(loc=2)

上图就是此例中要拟合的离散点，也是训练数据。

（二）定义网络

根据前述神经网络原理，可定义一个BPNN类如下：

import numpy as np
import numpy.matlib as matlib
import matplotlib.pyplot as plt
import numpy.random as random

class BPANN:
    '''
    1、定义一个各层神经元个数分别为neures=[k1, k2, ...]的神经网络，其中k1为作为输入的
       神经元个数。
    2、初始化入参W为由各神经元层之间的连接权重矩阵构成的数组；初始化入参B为由各神经元层
       的偏移向量构成的数组。均默认为随机数。
    3、每个神经元的激活函数默认为是Sigmoid函数。
	'''
	
    def __init__(self, neures, W=None, B=None):
        self.neures = neures
        self.W = []         # The weight matrixes of each neures layer
        self.B = []         # The bias vectors of each neures layer
        # Construct the matrixes of weight and bias of each neures layer
        for i in range(1, len(neures)):
            # A matrix of random floats follow standard normal distribution
            self.W.append(matlib.randn(neures[i], neures[i-1]))
            self.B.append(matlib.randn(neures[i], 1))

    # Activation function (Sigmoid function) of each neures
    def actFun(self, x):       # The input x should be considered as a vector
        return 1/(1+np.exp(-x))
    
    # Use the ANN to get the output
    def work(self, X, lowerLimit=0, upperLimit=1):
        # Check the type of input parameters
        if not all(isinstance(x, float) or isinstance(x, int) for x in X):
            raise Exception("the type of parameters must be float or int list")
        else:
            self.Z = []         # The input vectors of each neures layer 
            self.O = []         # The output vectors of each neures layer
            # The input vector of first neure layer
            self.Z.append(self.W[0]*np.matrix(X).T + self.B[0])
            # The output vector of first neure layer
            self.O.append(self.actFun(self.Z[-1]))
            for (w, b) in zip(self.W[1:], self.B[1:]):
                self.Z.append(w*self.O[-1] + b)
                self.O.append(self.actFun(self.Z[-1]))
            # Renormalize and change the type of output to a list
            return list((self.O[-1]*(upperLimit-lowerLimit)+lowerLimit).A1)
    
    # Train the ANN    
    def train(self, sampleX, sampleY, step, iterations=100, size=0):
        '''
        sampleX：所有不重复训练样本的入参，一个一维列表。
        sampleY：所有不重复训练样本的出参，一个与上述入参同长度的一维列表。
        step：每次训练迭代的步长，一个(0, 10)的数值。
        iterations：训练迭代倍数，乘以样本子集个数即为训练迭代次数，是一个大于零的整
                    数，默认是30倍。
        size：每次迭代从样本全集中抽取的样本子集大小，最小值是1，最大值不超过样本全集
              大小（若超过或值为0则取样本全集大小）的整数。
        '''
        # The indices list of the samples in the universal set
        self.uniSetIndices = list(range(0,len(sampleX)))
        random.shuffle(self.uniSetIndices)  # Disrupt the sort of samples
        # The list of the indices lists of the samples in each subset
        self.subsetsIndices = []
        if size > 0 and size <= len(sampleX):
            i = 0
            while i < len(sampleX):
                self.subsetsIndices.append(self.uniSetIndices[i: i+size])
                i = i + size
        else:
            self.subsetsIndices = [self.uniSetIndices]

        # Normalize the sampleY
        SYM = np.matrix(sampleY)
# Use each colume's max data to consturct a matrix that has the same shape
        maxData = matlib.ones((SYM.shape[0], 1)) * np.amax(SYM, axis=0)
# Use each colume's min data to consturct a matrix that has the same shape 
        minData = matlib.ones((SYM.shape[0], 1)) * np.amin(SYM, axis=0)
# Normal = (original - min)/(max - min)
        sampleY = np.nan_to_num(np.divide((SYM - minData),
                                    (maxData - minData)), nan=1).tolist()

        # The list of loss expectation of each iteration's eache subset
        J = []
        # The number of neures layers include the input layer
        layerNum = len(self.neures)
        while iterations > 0:                
            # Dispose each subset
            for sI in self.subsetsIndices:
                # The partial derivative matrixes of each neures layer's weight
                self.dW = []
                # The partial derivative vectors of each neures layer's bias
                self.dB = []
                # Construct all weight and bias matrixex filled by zero
                for i in range(1, layerNum):
                    self.dW.append(matlib.zeros((self.neures[i], 
                                                     self.neures[i-1])))
                    self.dB.append(matlib.zeros((self.neures[i], 1)))
                    
                # Dispose each sample in the subset
                L = 0             # The loss of all samples in the subset
                subSize = len(sI) # The size of the subset
                for i in sI:
                    # The sensitivity vectors of each neures layer
                    Delta = []
                    # Get the current state of the ANN
                    Y = np.matrix(self.work(sampleX[i])).T
                    # Recalculate the loss which is defined as sum of squared errors
                    L = L + 0.5*np.sum(np.square(Y-np.matrix(sampleY[i]).T))
                    # Get the sensitivity vectors of the last neure layer 
                    Delta.append(np.diag(np.multiply(self.O[-1],
                            (1-self.O[-1])).A1) * (Y-np.matrix(sampleY[i]).T))
                    for j in range(layerNum-2, 0, -1):
                        # Delta_j = diag[f'(Z_j)]*W_j.T*Delta_(j-1)
                        Delta.append(np.diag(np.multiply(self.O[j-1],
                                (1-self.O[j-1])).A1) * self.W[j].T*Delta[-1])
                    Delta.reverse()
                            
                    # Sum gradients at each sample in the subset
                    self.dW[0] = self.dW[0] + Delta[0