Spectral clustering（谱聚类）算法的实现

1.作者介绍

刘然，女，西安工程大学电子信息学院，2021级研究生
研究方向：图像处理
电子邮件：[email protected]

刘帅波，男，西安工程大学电子信息学院，2021级研究生，张宏伟人工智能课题组
研究方向：机器视觉与人工智能
电子邮件：[email protected]

2.关于谱聚类的介绍

2.1 谱聚类概述

谱聚类是从图论中演化出来的算法，它的主要思想是把所有的数据看做空间中的点，这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低，而距离较近的两个点之间的边权重值较高，通过对所有数据点组成的图进行切图，让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高，从而达到聚类的目的。

2.2 无向权重图

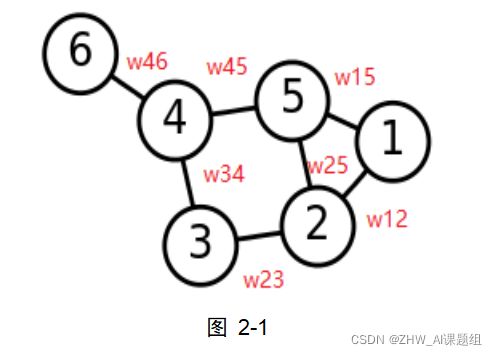
对于一个图G，我们一般用点的集合V和边的集合E来描述。即为G(V,E)。其中V即为我们数据集里面所有的点(v1,v2,…vn)。对于V中的任意两个点，点vi和点vj，我们定义权重wij为二者之间的权重。由于是无向图，所以wij=wji。

2.3 邻接矩阵

邻接矩阵(Adjacency Matrix):是表示顶点之间相邻关系的矩阵。在如图2-1所示的权重图当中（假设各权重为1），其邻接矩阵可表示为图2-2所示。

2.4 相似矩阵

在谱聚类中，我们只有数据点的定义，并没有直接给出这个邻接矩阵，所以我们可以通过样本点距离度量的相似矩阵S来获得邻接矩阵W。

2.5 度矩阵

度矩阵是对角阵，对角上的元素为各个顶点的度。图2-1的度矩阵为图2-3所示。

2.6 拉普拉斯矩阵

拉普拉斯矩阵L=D-W，其中D为度矩阵，W为邻接矩阵。图2-1的拉普拉斯矩阵为图2-4所示。

用拉普拉斯矩阵求解特征值，通过确定特征值（特征值要遵循从小到大的排列方式）的个数来确定对应特征向量的个数，从而实现降维，然后再用kmeans将特征向量进行聚类。

2.7 K-Means

K-Means是聚类算法中的最常用的一种，算法最大的特点是简单，好理解，运算速度快，但是只能应用于连续型的数据，并且一定要在聚类前需要手工指定要分成几类。
下面，我们描述一下K-means算法的过程，为了尽量不用数学符号，所以描述的不是很严谨，大概就是这个意思，“物以类聚、人以群分”：
1.首先输入k的值，即我们希望将数据集经过聚类得到k个分组。
2.从数据集中随机选择k个数据点作为初始大哥（质心，Centroid）
3.对集合中每一个小弟，计算与每一个大哥的距离（距离的含义后面会讲），离哪个大哥距离近，就跟定哪个大哥。
4.这时每一个大哥手下都聚集了一票小弟，这时候召开人民代表大会，每一群选出新的大哥（其实是通过算法选出新的质心）。
5.如果新大哥和老大哥之间的距离小于某一个设置的阈值（表示重新计算的质心的位置变化不大，趋于稳定，或者说收敛），可以认为我们进行的聚类已经达到期望的结果，算法终止。
6.如果新大哥和老大哥距离变化很大，需要迭代3~5步骤。

3.Spectral clustering（谱聚类）算法实现

3.1 数据集

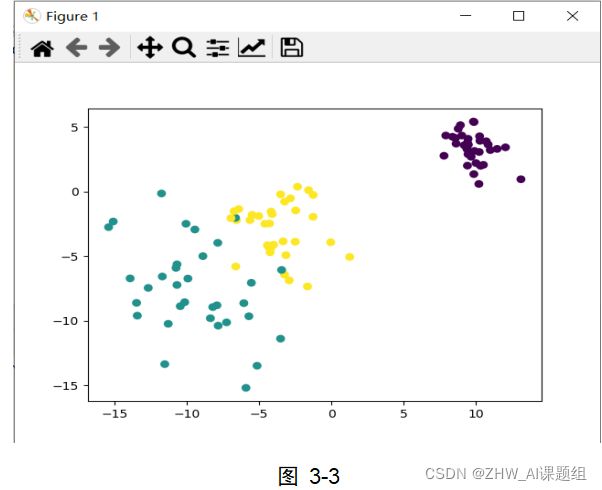
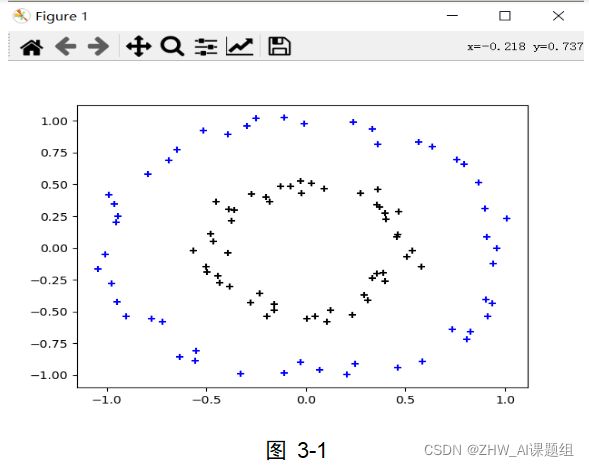
本实验中使用到的数据集均由sklearn.datasets中提供的方法生成，本实验中用到了make_circles，make_moons，make_blobs等函数。make_circles生成数据集，形成一个二维的大圆，包含一个小圆，如图3-1所示；make_moons生成数据集，形成两个弯月，如图3-2所示；make_blobs为聚类生成符合正态分布的数据集，如图3-3所示。

3.2 导入所需要的包

#导入需要的包
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_moons#生成数据集，形成两个弯月。
from sklearn.datasets import make_circles#生成数据集，形成一个二维的大圆，包含一个小圆
from sklearn.datasets import make_blobs#为聚类生成符合正态分布的数据集，产生一个数据集和相应的标签
import matplotlib.pyplot as plt

3.3 获取特征值和特征向量

def get_eigen(L, num_clusters):#获取特征
    eigenvalues, eigenvectors = np.linalg.eigh(L)#获取特征值  特征向量
    best_eigenvalues = np.argsort(eigenvalues)[0:num_clusters]#argsort函数返回的是数组值从小到大的索引值
    U = np.zeros((L.shape[0], num_clusters))
    U = eigenvectors[:, best_eigenvalues]#将这些特征取出 构成新矩阵
    return U

3.4 利用K-Means聚类

#K-Means聚类
def cluster(data, num_clusters):
    data = np.array(data)
    W = affinity_matrix(data)
    D = getD(W)
    L = getL(D, W)
    eigenvectors = get_eigen(L, num_clusters)
    clf = KMeans(n_clusters=num_clusters)
    s = clf.fit(eigenvectors)  # 聚类
    label = s.labels_
    return label

3.5 完整代码

#导入需要的包
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_moons#生成数据集，形成两个弯月。
from sklearn.datasets import make_circles#生成数据集，形成一个二维的大圆，包含一个小圆
from sklearn.datasets import make_blobs#为聚类生成符合正态分布的数据集，产生一个数据集和相应的标签
import matplotlib.pyplot as plt

#定义高斯核函数
def kernel(x1, x2, sigma_sq=0.05):
    return np.exp(-(np.linalg.norm(x1 - x2) ** 2) / (2 * sigma_sq ** 2))

#定义相似度矩阵
def affinity_matrix(X):
    A = np.zeros((len(X), len(X)))#零矩阵
    for i in range(len(X) - 1):#长度为len(x) 但是从0开始
        for j in range(i + 1, len(X)):#从1开始，到len(x) 是方阵 为啥下角标取值的初始值不同？？？
            A[i, j] = A[j, i] = kernel(X[i], X[j])
    return A#通过高斯核的计算 给矩阵赋予新值    10*10

# 计算度矩阵
def getD(A):
    D = np.zeros(A.shape)
    for i in range(A.shape[0]):
        D[i, i] = np.sum(A[i, :])
    return D

#计算拉普拉斯矩阵
def getL(D, A):
    L = D - A
    return L


def get_eigen(L, num_clusters):#获取特征
    eigenvalues, eigenvectors = np.linalg.eigh(L)#获取特征值  特征向量
    best_eigenvalues = np.argsort(eigenvalues)[0:num_clusters]#argsort函数返回的是数组值从小到大的索引值
    U = np.zeros((L.shape[0], num_clusters))
    U = eigenvectors[:, best_eigenvalues]#将这些特征取出 构成新矩阵
    return U

#K-Means聚类
def cluster(data, num_clusters):
    data = np.array(data)
    W = affinity_matrix(data)
    D = getD(W)
    L = getL(D, W)
    eigenvectors = get_eigen(L, num_clusters)
    clf = KMeans(n_clusters=num_clusters)
    s = clf.fit(eigenvectors)  # 聚类
    label = s.labels_
    return label


def plotRes(data, clusterResult, clusterNum):
    """
    结果可似化
    : data:  样本集
    : clusterResult: 聚类结果
    : clusterNum: 聚类个数
    :return:
    """
    n = len(data)
    scatterColors = ['black', 'blue', 'red', 'yellow', 'green', 'purple', 'orange']
    for i in range(clusterNum):
        color = scatterColors[i % len(scatterColors)]
        x1 = []
        y1 = []
        for j in range(n):
            if clusterResult[j] == i:
                x1.append(data[j, 0])
                y1.append(data[j, 1])
        plt.scatter(x1, y1, c=color, marker='+')


if __name__ == '__main__':
# # #月牙形数据集,sigma=0.1
# #     # cluster_num = 2
# #     # data, target = make_moons()
# #     # label = cluster(data, cluster_num)
# #     # print(label)
# #     # plotRes(data, label, cluster_num)
# #
#     # 圆形数据集,sigma=0.05
    cluster_num = 2
    data, target = make_circles(n_samples=1000, shuffle=True, noise=0.05, factor=0.5)
    label = cluster(data, cluster_num)
    print(label)
    plotRes(data, label, cluster_num)


# #
# #    #  # 正态数据集
# #    # # n_samples是待生成的样本的总数。
# #    #  # n_features是每个样本的特征数。
# #    #  # centers表示类别数。
# #    #  # cluster_std表示每个类别的方差，例如我们希望生成2类数据，其中一类比另一类具有更大的方差，可以将cluster_std设置为[1.0, 3.0]。
# #    #  cluster_num = 2
# #    #  data, target = make_blobs(n_samples=1500, n_features=2, centers=4, random_state=24)
# #    #  label = cluster(data, cluster_num)
# #    #  print(label)
# #    #  plt.subplot(121)
# #    #  plotRes(data, target, cluster_num)
# #    #  plt.subplot(122)
# #    #  plotRes(data, label, cluster_num)
# #
plt.show()

4.参考

1.<谱聚类（spectral clustering）原理总结 - 刘建平Pinard - 博客园
2.参考博客1
3.参考博客2
4.参考博客3