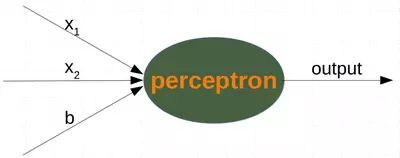
从零开始用 Python 构建一个简单的神经网络
线性可分数据集
正如我们在机器学习教程的前一章中所展示的,仅由一个感知器组成的神经网络足以分离我们的示例类。当然,我们精心设计了这些类以使其工作。有许多类集群,对于它们不起作用。我们将查看其他一些示例,并将讨论无法分离类的情况。
我们的类是线性可分的。线性可分性在欧几里得几何中有意义。两组点(或类)称为线性可分的,如果平面中至少存在一条直线,使得一类的所有点都在直线的一侧,而另一类的所有点都在另一侧边。
更正式的:
如果两个数据簇(类)可以通过线性方程形式的决策边界分开
∑一世=1nX一世⋅瓦一世=0
它们被称为线性可分。
否则,即如果这样的决策边界不存在,则这两个类被称为线性不可分。在这种情况下,我们不能使用简单的神经网络。
AND 函数的感知器
在我们的下一个示例中,我们将用 Python 编写一个神经网络,它实现逻辑“与”函数。它按以下方式为两个输入定义:
| 输入1 | 输入2 | 输出 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
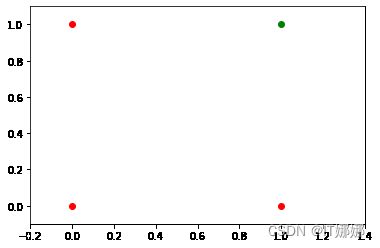
我们在上一章中了解到,具有一个感知器和两个输入值的神经网络可以解释为决策边界,即划分两个类别的直线。我们要在示例中分类的两个类如下所示:
将 matplotlib.pyplot 导入为 plt
将 numpy 导入为 np
图, ax = plt 。子图()
xmin , xmax = - 0.2 , 1.4
X = np 。arange ( xmin , xmax , 0.1 )
ax 。scatter ( 0 , 0 , color = "r" )
ax 。scatter ( 0 , 1 , color = "r" )
ax 。分散(1 , 0 , color = "r" )
ax 。scatter ( 1 , 1 , color = "g" )
ax 。set_xlim ([ xmin , xmax ])
ax 。set_ylim ([ - 0.1 , 1.1 ])
m = - 1
#ax.plot(X, m * X + 1.2, label="decision boundary")
plt . 情节()
输出:
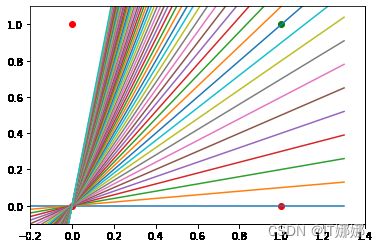
我们还发现,这样一个原始的神经网络只能创建穿过原点的直线。所以分割线是这样的:
将 matplotlib.pyplot 导入为 plt
将 numpy 导入为 np
图, ax = plt 。子图()
xmin , xmax = - 0.2 , 1.4
X = np 。arange ( xmin , xmax , 0.1 )
ax 。set_xlim ([ xmin , xmax ])
ax 。set_ylim ([ - 0.1 , 1.1 ])
m = - 1
for m in np 。范围(0 , 6 , 0.1 ):
ax 。绘图( X , m * X )
ax 。scatter ( 0 , 0 , color = "r" )
ax 。scatter ( 0 , 1 , color = "r" )
ax 。scatter ( 1 , 0 , color = "r" )
ax 。分散( 1, 1 , color = "g" )
plt . 情节()
输出:
我们可以看到,这些直线都不能用作决策边界,也不能用作穿过原点的任何其他直线。
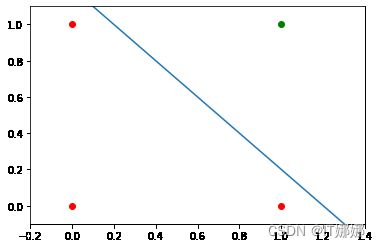
我们需要一条线
是=米⋅X+C其中截距c不等于 0。
例如线
是=-X+1.2
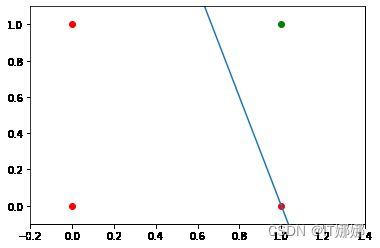
可以用作我们问题的分隔线:
将 matplotlib.pyplot 导入为 plt
将 numpy 导入为 np
图, ax = plt 。子图()
xmin , xmax = - 0.2 , 1.4
X = np 。arange ( xmin , xmax , 0.1 )
ax 。scatter ( 0 , 0 , color = "r" )
ax 。scatter ( 0 , 1 , color = "r" )
ax 。分散(1 , 0 , color = "r" )
ax 。scatter ( 1 , 1 , color = "g" )
ax 。set_xlim ([ xmin , xmax ])
ax 。set_ylim ([ - 0.1 , 1.1 ])
m , c = - 1 , 1.2
ax 。绘图( X , m * X + c )
PLT 。情节()
输出:
现在的问题是,我们能否找到对网络模型稍加修改的解决方案?或者换句话说:我们能否创建一个能够定义任意决策边界的感知器?
解决方案包括添加偏置节点。
具有偏差的单个感知器
具有两个输入值和一个偏差的感知器对应于一条一般直线。借助偏置值,b我们可以训练感知器来确定具有非零截距的决策边界c。
虽然输入值可以改变,但偏置值始终保持不变。只能调整偏置节点的权重。
现在,感知器的线性方程包含偏差:
∑一世=1n瓦一世⋅X一世+瓦n+1⋅乙=0
在我们的例子中,它看起来像这样:
瓦1⋅X1+瓦2⋅X2+瓦3⋅乙=0
这相当于
X2=-瓦1瓦2⋅X1-瓦3瓦2⋅乙
这意味着:
米=-瓦1瓦2
和
C=-瓦3瓦2⋅乙
import numpy as np
from collections import Counter
类 感知器:
def __init__ ( self ,
weights ,
bias = 1 ,
learning_rate = 0.3 ):
"""
'weights' 可以是一个 numpy 数组、列表或具有
权重实际值的
元组。输入值的数量 由'weights'
"""
self 的长度。权重 = np 。数组(权重)
自我。偏见 = 偏见
自我。学习率 = 学习率
@staticmethod
def unit_step_function ( x ):
如果 x <= 0 :
return 0
else :
return 1
def __call__ ( self , in_data ):
in_data = np 。串连( (IN_DATA , [自。偏压]) )
结果 = 自我。weights @ in_data
返回 感知器。unit_step_function (结果)
def 调整( self ,
target_result ,
in_data ):
if type ( in_data ) != np . ndarray :
in_data = np 。阵列(IN_DATA ) #
calculated_result = 自(IN_DATA )
误差 = target_result - calculated_result
如果 错误 =! 0 :
IN_DATA = NP 。连接( (in_data , [ self . 偏差]) )
校正 = 错误 * in_data * self 。learning_rate
自我。权重 += 修正
DEF 评估(自, 数据, 标签):
评价 = 计数器()
对于 样品, 标签 在 拉链(数据, 标签):
结果 = 自(样品) #预测
如果 结果 == 标签:
评价[ “正确” ] + = 1
否则:
评估[ “错误” ] += 1
返回 评估
我们假设上面带有 Perceptron 类的 Python 代码以“perceptrons.py”的名称存储在您当前的工作目录中。
import numpy as np
from perceptrons import Perceptron
def labelled_samples ( n ):
for _ in range ( n ):
s = np 。随机的。randint ( 0 , 2 , ( 2 ,))
yield ( s , 1 ) if s [ 0 ] == 1 and s [ 1 ] == 1 else ( s , 0 )
p = 感知器(权重= [ 0.3 , 0.3 , 0.3 ],
learning_rate = 0.2 )
对于 IN_DATA , 标签 在 labelled_samples (30 ):
p 。调整(标签,
输入数据)
test_data , test_labels = list ( zip ( * labelled_samples ( 30 )))
评价 = p 。评估(test_data , test_labels )
打印(评估)
输出:
计数器({'正确':30})
将 matplotlib.pyplot 导入为 plt
将 numpy 导入为 np
图, ax = plt 。子图()
xmin , xmax = - 0.2 , 1.4
X = np 。arange ( xmin , xmax , 0.1 )
ax 。scatter ( 0 , 0 , color = "r" )
ax 。scatter ( 0 , 1 , color = "r" )
ax 。分散(1 , 0 , color = "r" )
ax 。scatter ( 1 , 1 , color = "g" )
ax 。set_xlim ([ xmin , xmax ])
ax 。set_ylim ([ - 0.1 , 1.1 ])
m = - p 。权重[ 0 ] / p 。权重[ 1 ]
c = - p. 权重[ 2 ] / p 。weights [ 1 ]
打印( m , c )
ax 。绘图( X , m * X + c )
plt 。情节()
输出:
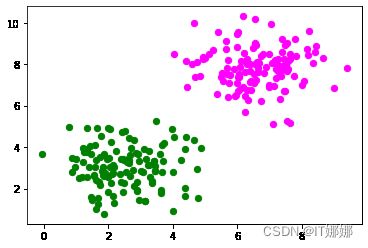
我们将创建另一个具有线性可分数据集的示例,该数据集需要一个偏置节点才能进行分离。我们将使用以下make_blobs函数sklearn.datasets:
从 sklearn.datasets 导入 make_blobs
n_samples = 250 个
样本, 标签 = make_blobs ( n_samples = n_samples ,
中心= ([ 2.5 , 3 ], [ 6.7 , 7.9 ]),
random_state = 0 )
让我们可视化之前创建的数据:
导入 matplotlib.pyplot 作为 plt
颜色 = ( 'green' , 'magenta' , 'blue' , 'cyan' , 'yellow' , 'red' )
fig , ax = plt . 子图()
用于 n_class 在 范围(2 ):
斧。分散(样本[标签== n_class ][:, 0 ], 样本[标签== n_class ][:, 1 ],
c =颜色[ n_class ], s = 40 , label = str ( n_class ))
n_learn_data = int ( n_samples * 0.8 ) # 80% 的可用数据点
learn_data , test_data = samples [: n_learn_data ], samples [ - n_learn_data :]
learn_labels , test_labels = labels [: n_learn_data ], labels [ - n_learn_data :]
从 感知器 导入 感知器
p = 感知器(权重= [ 0.3 , 0.3 , 0.3 ],
learning_rate = 0.8 )
为 样品, 标签 在 拉链(learn_data , learn_labels ):
p 。调整(标签,
样本)
评价 = p 。评估(学习数据, 学习标签)
打印(评估)
输出:
计数器({'正确':200})
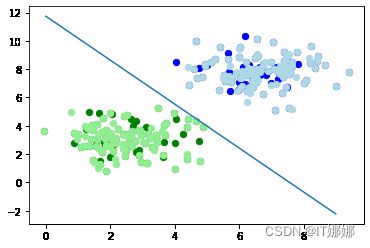
让我们可视化决策边界:
导入 matplotlib.pyplot 作为 plt
图, ax = plt 。子图()
# 绘制学习数据
colors = ( 'green' , 'blue' )
for n_class in range ( 2 ):
ax 。分散( learn_data [ learn_labels == n_class ][:, 0 ],
learn_data [ learn_labels == n_class ][:, 1 ],
c =颜色[ n_class ], s = 40 , label = str ( n_class))
# 绘制测试数据
colors = ( 'lightgreen' , ' lightblue ' )
for n_class in range ( 2 ):
ax . 分散( test_data [ test_labels == n_class ][:, 0 ],
test_data [ test_labels == n_class ][:, 1 ],
c =颜色[ n_class ], s = 40 , label = str ( n_class))
X = np 。arange ( np . max ( samples [:, 0 ]))
m = - p 。权重[ 0 ] / p 。权重[ 1 ]
c = - p 。权重[ 2 ] / p 。weights [ 1 ]
打印( m , c )
ax 。情节( X, m * X + c )
plt 。情节()
plt 。显示()
输出:
在下一节中,我们将介绍神经网络的 XOR 问题。它是非线性可分神经网络的最简单示例。它可以通过额外的神经元层来解决,称为隐藏层。
神经网络的异或问题
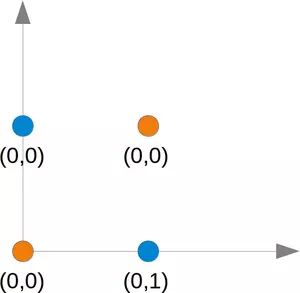
XOR(异或)函数由以下真值表定义:
| 输入1 | 输入2 | 异或输出 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
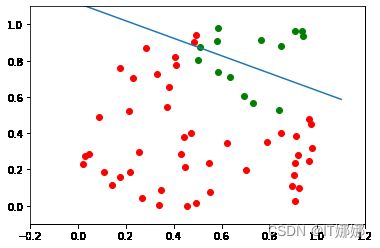
这个问题不能用简单的神经网络解决,如下图所示:
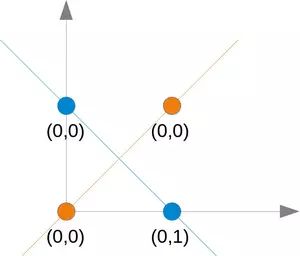
无论您选择哪条直线,您都不会成功地在一侧拥有蓝色点而在另一侧拥有橙色点。这如下图所示。橙色点位于橙色线上。这意味着这不能是一条分界线。如果我们平行移动这条线——无论朝哪个方向,总会有两个橙色和一个蓝色点在一侧,而在另一侧只有一个蓝色点。如果我们以非平行方式移动橙色线,则两侧将有一个蓝色和一个橙色点,除非该线通过橙色点。所以没有办法用一条直线来分隔这些点。
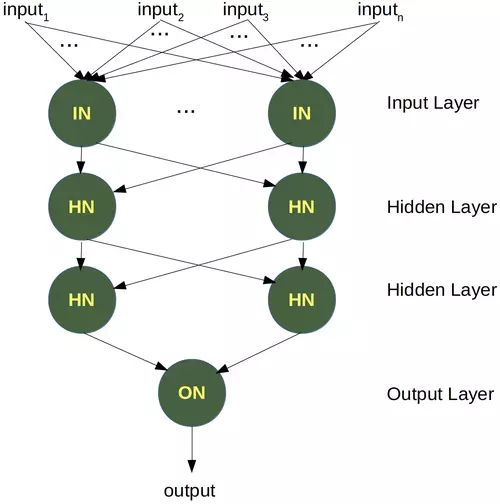
为了解决这个问题,我们需要引入一种新型的神经网络,一种具有所谓隐藏层的网络。隐藏层允许网络重新组织或重新排列输入数据。
我们只需要一个带有两个神经元的隐藏层。一个像与门一样工作,另一个像或门一样工作。当 OR 门触发而 AND 门不触发时,输出将“触发”。
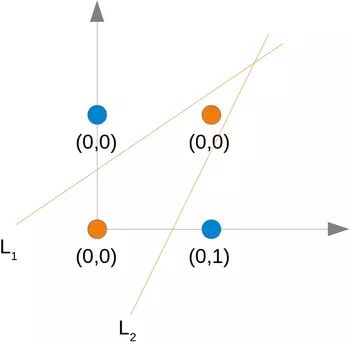
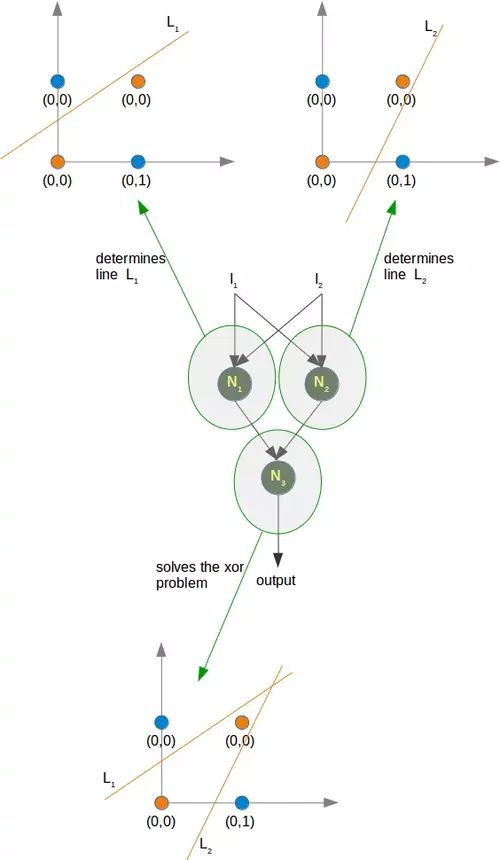
正如我们已经提到的,我们找不到将橙色点与蓝色点分开的线。但是它们可以用两条线分开,例如下图中的L 1和 L 2:
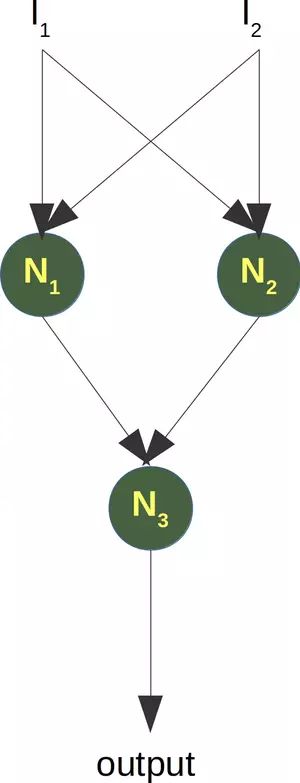
为了解决这个问题,我们需要以下类型的网络,即具有隐藏层 N 1和 N 2
神经元N 1将确定一条线,例如L 1并且神经元N 2将确定另一条线L 2。N 3最终会解决我们的问题:
在 Python 中实现这一点必须等到我们机器学习教程的下一章。
练习
练习 1
我们可以通过以下方式将逻辑 AND 扩展为 0 和 1 之间的浮点值:
| 输入1 | 输入2 | 输出 |
|---|---|---|
| x1 < 0.5 | x2 < 0.5 | 0 |
| x1 < 0.5 | x2 >= 0.5 | 0 |
| x1 >= 0.5 | x2 < 0.5 | 0 |
| x1 >= 0.5 | x2 >= 0.5 | 1 |
尝试训练一个只有一个感知器的神经网络。为什么不起作用?
练习 2
一个点属于 0 类,如果 X1<0.5 并且属于第 1 类,如果 X1>=0.5. 用一个感知器训练一个网络来对任意点进行分类。你对切割边界有什么看法?输入值怎么样X2
练习题解答
第一个练习的解决方案
从 感知器 导入 感知器
p = 感知器(权重= [ 0.3 , 0.3 , 0.3 ],
偏差= 1 ,
learning_rate = 0.2 )
def labelled_samples ( n ):
for _ in range ( n ):
s = np 。随机的。random (( 2 ,))
yield ( s , 1 ) if s [ 0 ] >= 0.5 and s [ 1 ] >= 0.5 else ( s , 0 )
对于 IN_DATA , 标签 在 labelled_samples (30 ):
p 。调整(标签,
输入数据)
test_data , test_labels = list ( zip ( * labelled_samples ( 60 )))
评价 = p 。评估(test_data , test_labels )
打印(评估)
输出:
计数器({'正确':52,'错误':8})
查看为什么它不起作用的最简单方法是将数据可视化。
将 matplotlib.pyplot 导入为 plt
将 numpy 导入为 np
ones = [ test_data [ i ] for i in range ( len ( test_data )) if test_labels [ i ] == 1 ]
zeroes = [ test_data [ i ] for i in range ( len ( test_data )) if test_labels [ i ] == 0 ]
图, ax = plt 。subplots ()
xmin , xmax = - 0.2 , 1.2
X , Y = list ( zip ( * ones ))
ax 。scatter ( X , Y , color = "g" )
X , Y = list ( zip ( * zeroes ))
ax 。散射( X , Y , color = "r" )
ax 。set_xlim ([ xmin , xmax ])
ax 。set_ylim ([ - 0.1 , 1.1 ])
c = - p 。权重[ 2 ] / p 。权重[ 1 ]
m = - p 。权重[ 0 ] / p 。权重[ 1 ]
X = NP . arange ( xmin , xmax , 0.1 )
ax 。绘图(X , m * X + c , 标签= “决策边界” )
输出:
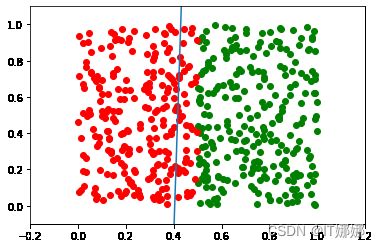
我们可以看到,绿点和红点不是一条直线。
第二个练习的解决方案
从 感知器 导入 感知器
import numpy as np
from collections import Counter
def labelled_samples ( n ):
for _ in range ( n ):
s = np 。随机的。random (( 2 ,))
yield ( s , 0 ) if s [ 0 ] < 0.5 else ( s , 1 )
p = 感知器(权重= [ 0.3 , 0.3 , 0.3 ],
learning_rate = 0.4 )
对于 IN_DATA , 标签 在 labelled_samples (300 ):
p 。调整(标签,
输入数据)
test_data , test_labels = list ( zip ( * labelled_samples ( 500 )))
打印(p 。权重)
p 。评估(test_data , test_labels )
输出:
[ 2.22622234 -0.05588858 -0.9 ]
计数器({'正确':460,'错误':40})
将 matplotlib.pyplot 导入为 plt
将 numpy 导入为 np
ones = [ test_data [ i ] for i in range ( len ( test_data )) if test_labels [ i ] == 1 ]
zeroes = [ test_data [ i ] for i in range ( len ( test_data )) if test_labels [ i ] == 0 ]
图, ax = plt 。subplots ()
xmin , xmax = - 0.2 , 1.2
X , Y = list ( zip ( * ones ))
ax 。scatter ( X , Y , color = "g" )
X , Y = list ( zip ( * zeroes ))
ax 。散射( X , Y , color = "r" )
ax 。set_xlim ([ xmin , xmax ])
ax 。set_ylim ([ - 0.1 , 1.1 ])
c = - p 。权重[ 2 ] / p 。权重[ 1 ]
m = - p 。权重[ 0 ] / p 。权重[ 1 ]
X = NP . arange ( xmin , xmax , 0.1 )
ax 。绘图(X , m * X + c , 标签= “决策边界” )
输出:
p 。权重, 米
输出:
(数组([ 2.22622234, -0.05588858, -0.9 ]), 39.83322163376969)
m在这种情况下,斜率必须越来越大。