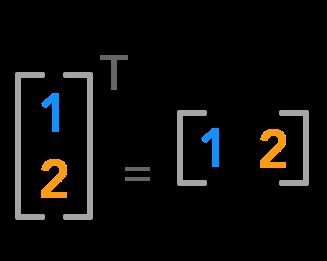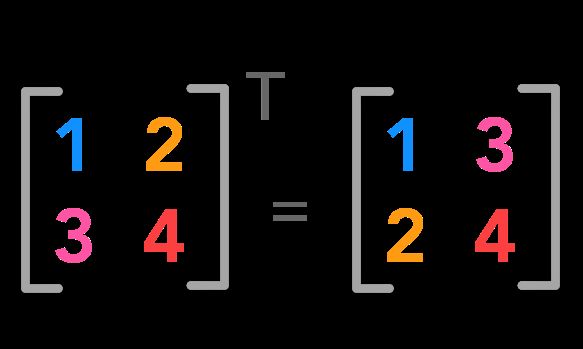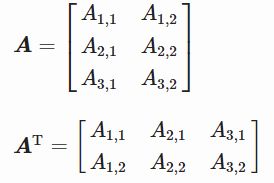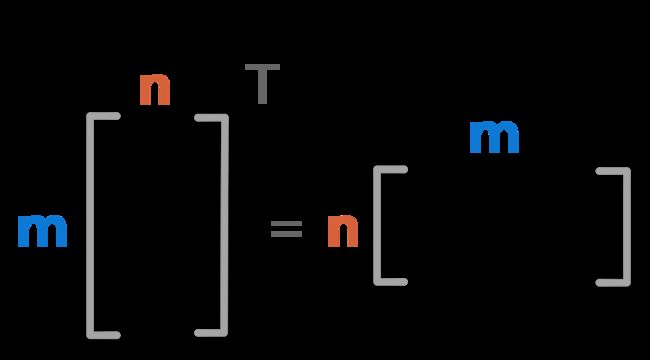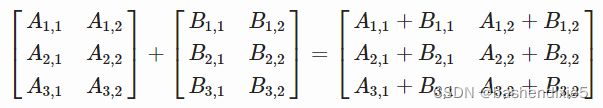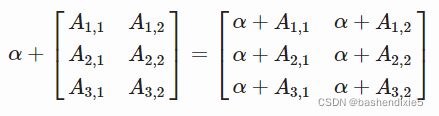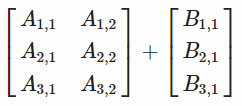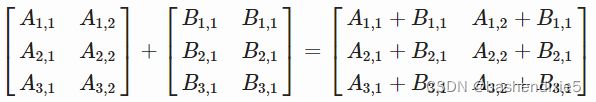机器学习笔记 - 标量、向量、矩阵、张量
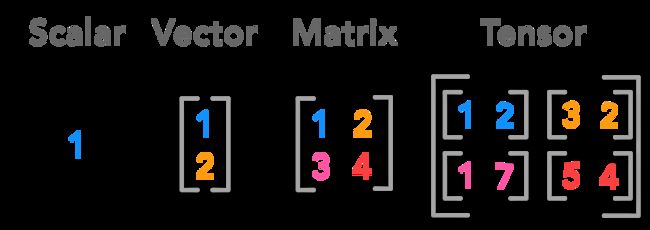
一、标量、向量、矩阵、张量
标量（Scalar）为一个数字。
向量（Vector）是一个数字数组。
矩阵（Matrix）是二维数组。
张量（Tensor）是一个n维数组n > 2。
标量、向量、矩阵和张量之间的区别
二、使用 Python 和 Numpy 创建向量
1、创建一个一维数组
x = np.array([1, 2, 3, 4])2、创建一个 (3x2) 矩阵
A = np.array([[1, 2], [3, 4], [5, 6]])3、数组的形状
print(A.shape)
print(x.shape)输出
(3, 2)
(4,)4、转置
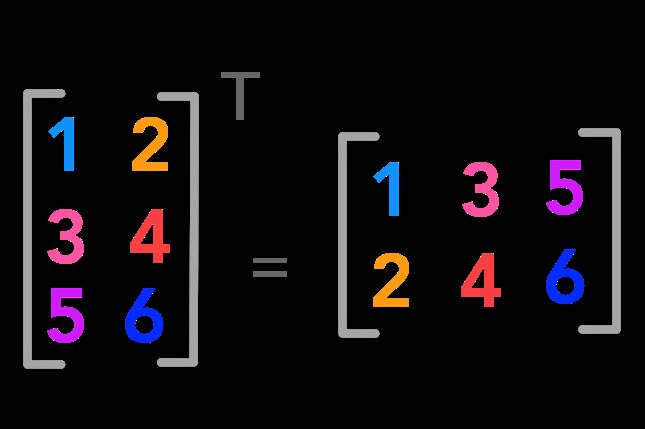
通过转置，您可以将行向量转换为列向量，反之亦然：
向量转置
方阵转置
非方阵转置
上标T用于转置矩阵。
形状 （m×n) 转置后变成 (n×m)。
矩阵转置的维度
转置示例代码
A = np.array([[1, 2], [3, 4], [5, 6]])
print(A)
A_t = A.T
print(A_t)打印如下
[[1 2]
[3 4]
[5 6]]
(3, 2)
[[1 3 5]
[2 4 6]]
(2, 3)5、相加
两个矩阵相加
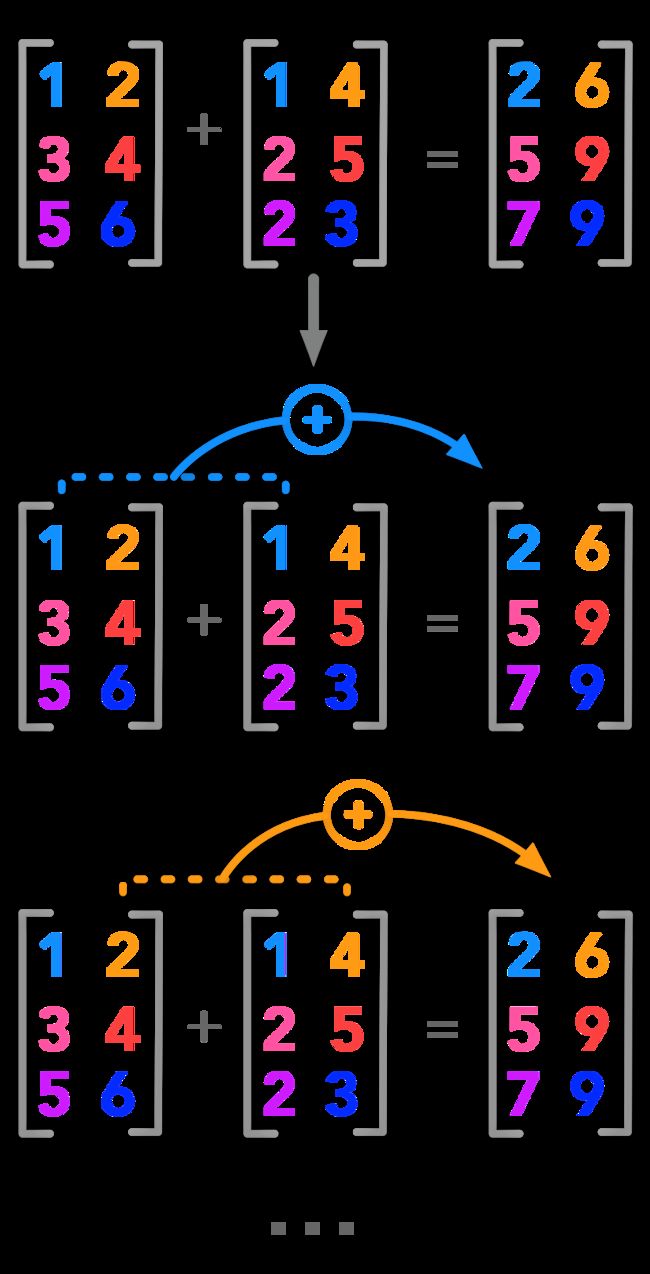
如果矩阵具有相同的形状，则可以进行相加。
示例代码
A = np.array([[1, 2], [3, 4], [5, 6]])
B = np.array([[2, 5], [7, 4], [4, 3]])
C = A + B
print(C)打印如下
[[ 3, 7],
[10, 8],
[ 9, 9]]也可以将标量添加到矩阵。
示例代码
A = np.array([[1, 2], [3, 4], [5, 6]])
C = A+4
print(C)打印如下
[[ 5, 6],
[ 7, 8],
[ 9, 10]]6、广播
Numpy 可以处理不同形状数组的操作。 较小的阵列将被扩展以匹配较大阵列的形状。 优点是这是在 C 中完成的（就像 Numpy 中的任何矢量化操作一样）。 实际上，我们在上一个示例中（标量与矩阵相加）使用了广播。标量被转换为与 A 形状相同的数组。
比如下面的例子：
等价于
如果形状可以匹配，Numpy 会自动执行此操作，如果不匹配，会报错。
示例代码
A = np.array([[1, 2], [3, 4], [5, 6]])
B = np.array([[2], [4], [6]])
C=A+B
print(C)打印如下
[[ 3 4]
[ 7 8]
[11 12]]如果是如下代码
A = np.array([[1, 2], [3, 4], [5, 6]])
B = np.array([[2], [4], [6], [8]])
C=A+B会报如下错误
ValueError: operands could not be broadcast together with shapes (3,2) (4,1)