数据分析-模型选择-数据集划分-交叉验证
目录
K折交叉检验
分层k折交叉验证
案例
0)导入必要的数据包
1)读入数据文件
2)数据探索
3)特征标签分离
4) 导入数据集划分库
5)可视化K折划分,k=5
6)可视化乱序后,K折划分,k=5
7)可视化层次k折划分,k=3
8) 可视化乱序k次
9)交叉验证
线性回归
逻辑回归
机器学习建模通常要对数据集进行划分,如sklearn.model_select的train_test_split方法,一部分数据用于训练模型,一部分数据用于对训练好的模型测试,评估模型的性能。数据集的不同划分会导致模型的训练效果不同。为了更好的训练模型,更可靠的评价模型性能。sklearn提供了多种数据集的划分与使用方法。这些方法集中在sklearn的model_select中,主要包含:KFold,ShuffleSplit,StratifiedKFold等。
K折交叉检验(KFold)
将数据集K折划分,下图为5折。每次采用不同的数据集对模型进行训练,并评估模型的性能。通过多次的训练,使得数据集中的每一个部分都作为数据集参加过模型训练,也作为测试集验证模型的性能。 多次训练的性能均值作为模型的最终性能。
K折交叉检验需要训练k个模型,增加了计算成本 ,但比单次划分训练集和测试集的方法更加稳定、全面。
如果数据集中相同标签的样本连续存放,如前面的全为0类,后面的全为1类,可能会导致某次的训练集全部为0类,而测试集全为1类。这样会导致模型的训练效果以及性能评价都不可靠。
分层k折交叉验证 (StratifiedKFold)
分层k折交叉验证使每个折类别之间的比例与整个数据集中的类别比例相同。采用分层k折交叉验证时根据标签划分,通常用于分类。
案例
0)导入必要的数据包
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import pandas as pd
import warnings
warnings.filterwarnings("ignore")1)读入数据文件
数据集包含30个样本,一个特征。特征“Education”为教育投入。标签“Income”为成年后年收入。
data=pd.read_csv("d:/datasets/Income1.csv",index_col="Unnamed: 0")
data=data.sample(len(data)) #乱序,原始数据label为连续型,递增
2)数据探索
data.head()| Education | Income | |
|---|---|---|
| 1 | 10.000000 | 26.658839 |
| 2 | 10.401338 | 27.306435 |
| 3 | 10.842809 | 22.132410 |
| 4 | 11.244147 | 21.169841 |
| 5 | 11.645485 | 15.192634 |
data.describe()| Education | Income | |
|---|---|---|
| count | 30.000000 | 30.000000 |
| mean | 16.000000 | 50.145469 |
| std | 3.642965 | 21.141553 |
| min | 10.000000 | 15.192634 |
| 25% | 12.989967 | 29.078897 |
| 50% | 16.000000 | 49.871749 |
| 75% | 19.010033 | 71.140149 |
| max | 22.000000 | 80.260571 |
data.info()Int64Index: 30 entries, 1 to 30 Data columns (total 2 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 Education 30 non-null float64 1 Income 30 non-null float64 dtypes: float64(2) memory usage: 720.0 bytes
3)特征标签分离
X=data["Education"]
y=data["Income"]4) 导入数据集划分库
from sklearn.model_selection import KFold
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import StratifiedKFold
5)可视化K折划分,k=5
每次选其中一折作为测试集,其它为训练集,
kf=KFold(n_splits=5) #K折划分
kf_cv=kf.split(X)
k=1
plt.figure(figsize=(16,5))
for train_indices, test_indices in kf_cv:
plt.scatter(train_indices,[k]*len(train_indices),marker=".",c="r")
plt.scatter(test_indices,[k]*len(test_indices),marker="+",c="b")
print("训练集索引-%d"%k,train_indices)
print("测试集索引-%d"%k,test_indices)
k=k+1
plt.yticks([1,2,3,4,5],["1","2","3","4","5"])
plt.ylabel("iteration")
plt.xlabel("index")训练集索引-1 [ 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29] 测试集索引-1 [0 1 2 3 4 5] 训练集索引-2 [ 0 1 2 3 4 5 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29] 测试集索引-2 [ 6 7 8 9 10 11] 训练集索引-3 [ 0 1 2 3 4 5 6 7 8 9 10 11 18 19 20 21 22 23 24 25 26 27 28 29] 测试集索引-3 [12 13 14 15 16 17] 训练集索引-4 [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 24 25 26 27 28 29] 测试集索引-4 [18 19 20 21 22 23] 训练集索引-5 [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23] 测试集索引-5 [24 25 26 27 28 29]
注:测试集的分布连续,每次使用的测试集完全不一样。
6)可视化乱序后,K折划分,k=5
每次选其中一折作为测试集,其它为训练集,
kfs=KFold(n_splits=5,random_state=10,shuffle=True) #K划分,乱序
kfs_cv=kfs.split(X)
k=1
plt.figure(figsize=(16,5))
for train_indices, test_indices in kfs_cv:
plt.scatter(train_indices,[k]*len(train_indices),marker=".",c="r")
plt.scatter(test_indices,[k]*len(test_indices),marker="+",c="b")
print("训练集索引-%d"%k,train_indices)
print("测试集索引-%d"%k,test_indices)
k=k+1
plt.yticks([1,2,3,4,5],["1","2","3","4","5"])
plt.ylabel("iteration")
plt.xlabel("index")训练集索引-1 [ 0 1 4 6 8 9 10 11 12 13 14 15 16 17 18 19 22 23 24 25 26 27 28 29] 测试集索引-1 [ 2 3 5 7 20 21] 训练集索引-2 [ 0 2 3 4 5 6 7 8 9 10 11 15 16 17 18 20 21 22 23 24 25 26 28 29] 测试集索引-2 [ 1 12 13 14 19 27] 训练集索引-3 [ 0 1 2 3 4 5 7 8 9 10 12 13 14 15 16 17 19 20 21 22 25 26 27 29] 测试集索引-3 [ 6 11 18 23 24 28] 训练集索引-4 [ 0 1 2 3 4 5 6 7 9 11 12 13 14 15 16 17 18 19 20 21 23 24 27 28] 测试集索引-4 [ 8 10 22 25 26 29] 训练集索引-5 [ 1 2 3 5 6 7 8 10 11 12 13 14 18 19 20 21 22 23 24 25 26 27 28 29] 测试集索引-5 [ 0 4 9 15 16 17]
注:测试集的分布不连续,且每次使用的测试集完全不一样。
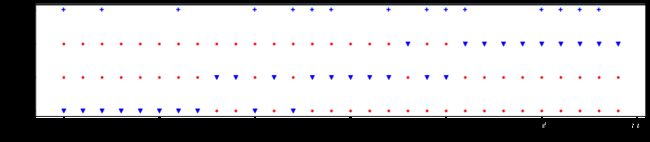
7)可视化层次k折划分,k=3
层次k折划分,每次选其中一折作为测试集,其它为训练集,确保在每次划分时不同类别的样本在测试集与训练集中比例划分,分层根据标签y实现,y为类别标签。
层次k折,是按标签划分。本数据集的标签(收入)为连续性数值,适合做回归。对标签Income离散化为高收入与低收入,将回归问题变为分类问题。
from sklearn.preprocessing import Binarizer
Bi_=Binarizer(threshold=50)
y1=Bi_.fit_transform(data[["Income"]]) #y1为离散化的标签,0,1skf_cv=skf.split(X,y1)
kk=[k*j for k,j in enumerate(y1) if j!=0]
k=1
plt.figure(figsize=(16,3))
for train_indices, test_indices in skf_cv:
plt.scatter(train_indices,[k]*len(train_indices),marker=".",c="r")
plt.scatter(test_indices,[k]*len(test_indices),marker="v",c="b")
print("训练集索引-%d"%k,train_indices)
print("测试集索引-%d"%k,test_indices)
k=k+1
plt.scatter(kk,[k]*len(kk),marker="+",c="b")
plt.yticks([1,2,3,4],["1","2","3","label"])
plt.ylabel("iteration")
plt.xlabel("index")训练集索引-1 [ 8 9 11 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29] 测试集索引-1 [ 0 1 2 3 4 5 6 7 10 12] 训练集索引-2 [ 0 1 2 3 4 5 6 7 10 12 18 21 22 23 24 25 26 27 28 29] 测试集索引-2 [ 8 9 11 13 14 15 16 17 19 20] 训练集索引-3 [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 19 20] 测试集索引-3 [18 21 22 23 24 25 26 27 28 29]
label为样本标签,图中“+”,表示对应index的样本类别为“1”,其它为“0”。
8) 可视化乱序k次
ShuffleSplit,将数据拆分为训练集和测试集,返回对应的索引。test_size缺省的大小为0.1
Shs=ShuffleSplit(n_splits=3,random_state=10) #乱序,划分3次,缺省测试集大小为0.1
Shs_cv=Shs.split(X)
k=1
plt.figure(figsize=(16,3))
for train_indices, test_indices in Shs_cv:
plt.scatter(train_indices,[k]*len(train_indices),marker=".",c="r")
plt.scatter(test_indices,[k]*len(test_indices),marker="+",c="b")
print("训练集索引-%d"%k,train_indices)
print("测试集索引-%d"%k,test_indices)
k=k+1
plt.yticks([1,2,3],["1","2","3"])
plt.ylabel("iteration")
plt.xlabel("index")训练集索引-1 [ 2 3 21 13 27 12 1 19 14 18 6 11 23 24 28 22 10 26 29 8 25 16 17 0 15 4 9] 测试集索引-1 [20 7 5] 训练集索引-2 [17 5 14 16 27 21 24 23 8 7 6 0 2 15 9 10 11 26 18 4 1 12 22 29 25 19 13] 测试集索引-2 [20 3 28] 训练集索引-3 [16 3 17 5 23 27 1 9 26 19 14 25 0 11 10 6 21 13 15 8 2 22 12 18 28 24 7] 测试集索引-3 [20 4 29]
注:
注意:与其他交叉验证策略不同,随机拆分不保证每次的划分都完全不同。上例可看到测试集中样本20被反复使用。
9)交叉验证
线性回归
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
print(cross_val_score(LinearRegression(),X,y,cv=5))[0.78595212 0.89966615 0.92784245 0.74751563 0.97521422]
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
print(cross_val_score(LinearRegression(),X,y,cv=kf))[0.78595212 0.89966615 0.92784245 0.74751563 0.97521422]
逻辑回归
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
print(cross_val_score(LogisticRegression(),X,y1,cv=Shs))[0.80443214 0.88889234 0.7805359 ]
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
print(cross_val_score(LogisticRegression(),X,y1,cv=5))[0.83333333 1. 1. 1. 1. ]