层次聚类算法的实现

1.作者介绍

杨金花，女，西安工程大学电子信息学院，21级硕士研究生
研究方向：基于学习方法的运动目标检测
电子邮件：[email protected]

孟莉苹，女，西安工程大学电子信息学院，2021级硕士研究生，张宏伟人工智能课题组
研究方向：机器视觉与人工智能
电子邮件：[email protected]

2．层次聚类算法介绍

2.1 层次聚类算法原理

 聚类就是对大量未知标注的数据集，按照数据内部存在的数据特征将数据集划分为多个不同的类别，使类别内的数据比较相似，类别之间的数据相似度比较小。
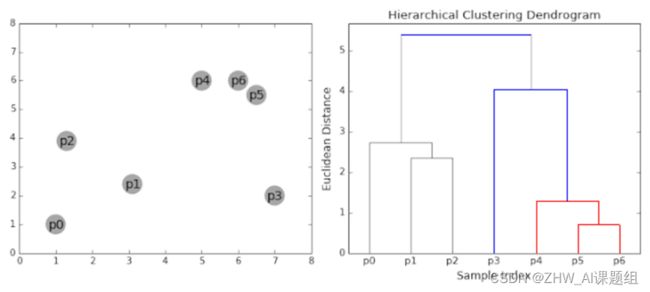
 层次聚类(Hierarchical Clustering)是聚类算法的一种，通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。在聚类树中，不同类别的原始数据点是树的最低层，树的顶层是一个聚类的根节点。创建聚类树有自下而上合并和自上而下分裂两种方法。算法流程展示如图所示。

2.2 层次聚类算法步骤

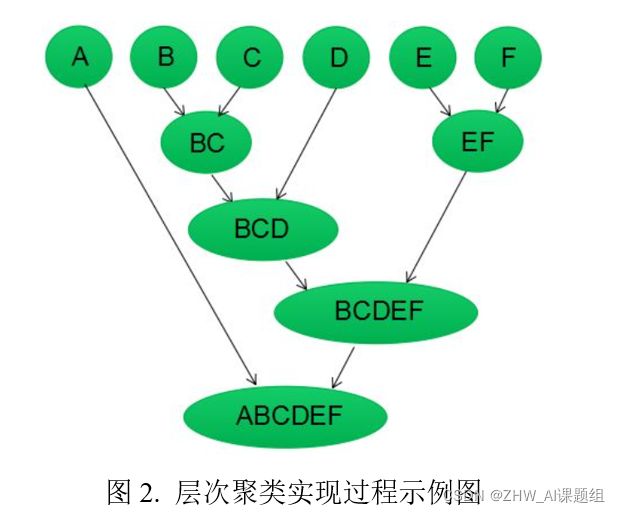
假设有6个样本点{A,B,C,D,E,F}，对于层次聚类来说，步骤如下：
（1）假设每个样本点都为一个簇类，计算每个簇类间的相似度，得到相似矩阵；
（2）寻找各个类之间最近的两个类，即若B和C的相似度最高，合并簇类B和C为一个簇类。现在我们还有五个簇类，分别为A，BC，D，E，F；
（3）更新簇类间的相似矩阵，若簇类BC和D的相似度最高，合并簇类BC和D为一个簇类。现在我们还有四个簇类，分别为A，BCD，E，F；
（4）更新簇类间的相似矩阵，若簇类E和F的相似度最高，合并簇类E和F为一个簇类。现在我们还有3个簇类，分别为A，BCD，EF。
（5）重复第四步，簇类BCD和簇类EF的相似度最高，合并该两个簇类，现在我们还有2个簇类，分别为A，BCDEF。
（6）最后合并簇类A和BCDEF为一个簇类，层次聚类算法结束。
层次聚类实现过程如图2所示。

2.3 层次聚类算法分类

自顶向下的层次聚类算法(Divisive)：
Divisive 层次聚类：又称自顶向下（top-down）的层次聚类，最开始所有的对象均属于一个cluster，每次按一定的准则将某个cluster 划分为多个cluster，如此往复，直至每个对象均属于某一个cluster。实现过程示意图如下。

自底向上的层次聚类算法(Agglomerative)：
Agglomerative 层次聚类：又称自底向上（bottom-up）的层次聚类，每一个对象最开始都是一个cluster，每次按一定的准则将最相近的两个cluster合并生成一个新的cluster，如此往复，直至最终所有的对象都属于一个cluster。

3．层次聚类算法实现(代码如下)

3.1 相关包导入

from scipy.cluster.hierarchy import linkage     #导入linage函数用于层次聚类
from scipy.cluster.hierarchy import dendrogram  #dendrogram函数用于将聚类结果绘制成树状图
from scipy.cluster.hierarchy import fcluster    #fcluster函数用于提取出聚类的结果
from sklearn.datasets import make_blobs         #make_blobs用于生成聚类算法的测试数据
from sklearn.cluster import AgglomerativeClustering  #自底向上层次聚类算法
import matplotlib.pyplot as plt                 #导入matplotlib绘图工具包

3.2 生成测试数据集

#生成测试数据
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4, random_state=0)
plt.figure(figsize=(10, 8))
plt.scatter(X[:, 0], X[:, 1], c='b')
plt.show()
#from scipy.cluster.hierarchy import linkage

3.3 层次聚类实现&画出树状图

#层次聚类实现
#from scipy.cluster.hierarchy import dendrogram
Z = linkage(X,  method='ward', metric='euclidean')
print(Z.shape)
print(Z[: 5])

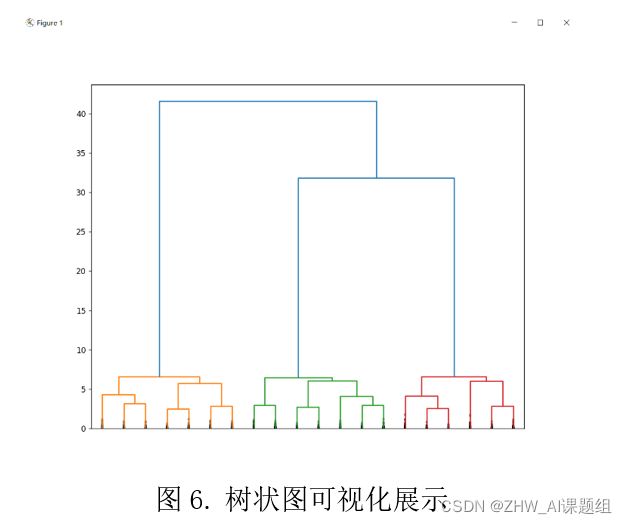
#画出树状图
#from scipy.cluster.hierarchy import fcluster
plt.figure(figsize=(10, 8))
dendrogram(Z, truncate_mode='lastp', p=20, show_leaf_counts=False, leaf_rotation=90, leaf_font_size=15,
           show_contracted=True)
plt.show()

3.4 获取聚类结果

#根据临界距离返回聚类结果
d = 15
labels_1 = fcluster(Z, t=d, criterion='distance')
print(labels_1[: 100])  # 打印聚类结果
print(len(set(labels_1)))  # 看看在该临界距离下有几个 cluster

#根据聚类数目返回聚类结果
k = 3
labels_2 = fcluster(Z, t=k, criterion='maxclust')
print(labels_2[: 100])
list(labels_1) == list(labels_2)  # 看看两种不同维度下得到的聚类结果是否一致

#聚类的结果可视化，相同的类的样本点用同一种颜色表示
plt.figure(figsize=(10, 8))
plt.scatter(X[:, 0], X[:, 1], c=labels_2, cmap='prism')
plt.show()

3.5完整代码

from scipy.cluster.hierarchy import linkage     #导入linage函数用于层次聚类
from scipy.cluster.hierarchy import dendrogram  #dendrogram函数用于将聚类结果绘制成树状图
from scipy.cluster.hierarchy import fcluster    #fcluster函数用于提取出聚类的结果
from sklearn.datasets import make_blobs         #make_blobs用于生成聚类算法的测试数据
from sklearn.cluster import AgglomerativeClustering  #自底向上层次聚类算法
import matplotlib.pyplot as plt                 #导入matplotlib绘图工具包

#生成测试数据
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4, random_state=0)
plt.figure(figsize=(10, 8))
plt.scatter(X[:, 0], X[:, 1], c='b')
plt.show()
#from scipy.cluster.hierarchy import linkage

#层次聚类实现
#from scipy.cluster.hierarchy import dendrogram
Z = linkage(X,  method='ward', metric='euclidean')
print(Z.shape)
print(Z[: 5])


#画出树状图
#from scipy.cluster.hierarchy import fcluster
plt.figure(figsize=(10, 8))
dendrogram(Z, truncate_mode='lastp', p=20, show_leaf_counts=False, leaf_rotation=90, leaf_font_size=15,
           show_contracted=True)
plt.show()

# 根据临界距离返回聚类结果
d = 15
labels_1 = fcluster(Z, t=d, criterion='distance')
print(labels_1[: 100])  # 打印聚类结果
print(len(set(labels_1)))  # 看看在该临界距离下有几个 cluster

# 根据聚类数目返回聚类结果
k = 3
labels_2 = fcluster(Z, t=k, criterion='maxclust')
print(labels_2[: 100])
list(labels_1) == list(labels_2)  # 看看两种不同维度下得到的聚类结果是否一致

# 聚类的结果可视化，相同的类的样本点用同一种颜色表示
plt.figure(figsize=(10, 8))
plt.scatter(X[:, 0], X[:, 1], c=labels_2, cmap='prism')
plt.show()

3.6 对比不同方法聚类效果

from time import time
import numpy as np
from sklearn.datasets import make_blobs
from scipy.cluster.hierarchy import linkage, fcluster
from sklearn.metrics.cluster import adjusted_mutual_info_score
import matplotlib.pyplot as plt

#生成样本点
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels = make_blobs(n_samples=750, centers=centers,
                       cluster_std=0.4, random_state=0)


#可视化聚类结果
def plot_clustering(X, labels, title=None):
    plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='prism')
    if title is not None:
        plt.title(title, size=17)
    plt.axis('off')
    plt.tight_layout()

#进行 Agglomerative 层次聚类
linkage_method_list = ['single', 'complete', 'average', 'ward']

plt.figure(figsize=(10, 8))
ncols, nrows = 2, int(np.ceil(len(linkage_method_list) / 2))
plt.subplots(nrows=nrows, ncols=ncols)
for i, linkage_method in enumerate(linkage_method_list):
    print('method %s:' % linkage_method)
    start_time = time()
    Z = linkage(X, method=linkage_method)
    labels_pred = fcluster(Z, t=3, criterion='maxclust')
    print('Adjust mutual information: %.3f' % adjusted_mutual_info_score(labels, labels_pred))
    print('time used: %.3f seconds' % (time() - start_time))
    plt.subplot(nrows, ncols, i + 1)
    plot_clustering(X, labels_pred, '%s linkage' % linkage_method)
plt.show()

AMI评估结果：
该量越接近于 1 则说明聚类算法产生的类越接近于真实情况。从右图的AMI量的表现来看，Single-link 方法下的层次聚类结果最差，它几乎将所有的点都聚为一个 cluster，而其他两个 cluster 则都仅包含个别稍微有点偏离中心的样本点，而另外三种聚类方法效果都还可以。结果如下图

4.参考链接

博客参考链接：
https://cloud.tencent.com/developer/article/1800586