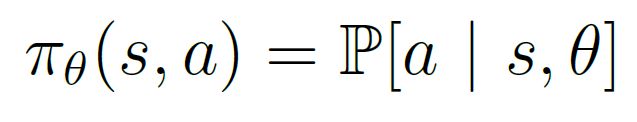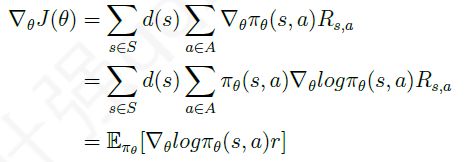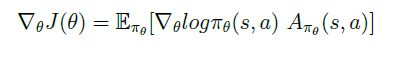强化学习知识要点与编程实践(6)——基于策略梯度的深度强化学习
基于策略梯度的深度强化学习
- 0. 引言
- 1. 基于策略学习的意义
- 2. 策略目标函数
- 3. Actor-Critic算法
- 4. 深度确定性策略梯度(DDPG)算法
- 5. 编程实践
本文未经许可,禁止转载,如需转载请联系笔者
0. 引言
前一章《价值函数的近似表示(含DQN算法)》中介绍了在强化学习中如何处理状态数量多或者状态连续时的情况,其基本思路就是构建一个价值近似函数(通常是一个神经网络),输入 是状态矢量(矢量的每个元素可以取连续值,元素数量即为神经网络的输入神经元个数)或状态矢量+动作,输出 是V值或Q值,如下图所示。
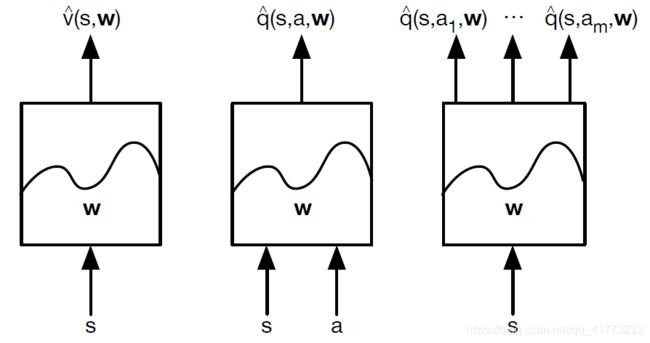
依据上面的思路,这也就诞生了DQN和DDQN算法,这两种算法的区别也可以见《图解DQN,DDQN,DDPG网络》
上面的方法只解决了状态连续的问题,却没解决动作连续的问题。假设动作连续,那么由神经网络的输出神经元数量=动作数量可知,输出神经元数量为无穷个,这显然是不可能的。因此诞生了 Actor-Critic 算法 与 DDPG算法 来解决连续动作空间和连续状态空间的问题。
前一章又被称为基于价值的学习,这一章是基于策略的学习。所谓策略(policy),就是根据输入状态 s s s,得出相应的输出动作 a a a。
在实际应用中通过建立分别对于 状态价值的近似函数 和 策略函数,使得一方面可以基于价值函数进行策略评估和优化,另一方面优化的策略函数又会使得价值函数更加准确的反应状态的价值,两者相互促进最终得到最优策略。
在这一思想背景下产生的 深度确定性策略梯度(DDPG) 算法成功地解决了连续行为空间中的诸多实际问题。
1. 基于策略学习的意义
正如引言所说,基于近似价值函数 的学习可以较高效率地解决 连续状态空间 的强化学习问题,但其 行为空间仍然是离散 的。
拿PuckWorld 世界环境来说,在上一章的编程实践中,个体在环境中有5个行为可供选择,分别是:上下左右与不动,而推力也是固定的1,因此这就是五个离散的动作。但是如果考虑更一般的推力情况,那就需要用一个二维的力矢量表示,而力矢量的两个元素是可以连续取值的,此时 基于近似价值函数 就无能为力了。
基于价值函数的学习有以下三个缺点:
-
不能解决动作连续的问题。原因如前所述。
-
对于状态观测的特征不够多的情况,它不能得到最优解。比如在构建状态特征矢量时,很可能因为我们的先验知识不足,在实际学习过程中出现了状态特征矢量相同,但是实际的状态不同的情况,那么这时基于价值函数的学习容易将我们带入误区。
-
基于价值的学习对应的最优策略通常是确定性策略,因为其是从众多行为价值中选择一个最大价值的行为,而有些问题的最优策略却是随机策略,这种情况下同样是无法通过基于价值的学习来求解的。
可以看出,基于价值的强化学习虽然能出色地解决很多问题,但面对行为空间连续、观测受限、随机策略的学习等问题时仍然显得力不从心。此时 基于策略的学习 是解决这类问题的一个新的途径。在基于策略的强化学习中,策略 π \pi π可以被被描述为一个包含参数 θ \theta θ的函数:
策略函数 π θ \pi_{\theta} πθ确定了在 给定的状态 和 一定的参数设置 下,采取任何可能行为的概率,是一个概率密度函数。在实际应用这个策略时,选择最大概率对应的行为或者以此为基础进行一定程度的采样探索。
可以认为,参数 θ \theta θ决定了策略的具体形式。因而求解基于策略的学习问题就转变为了如何确定策略函数的参数 θ \theta θ。同样可以通过设计一个基于参数 θ \theta θ的目标函数 J ( θ ) J(\theta) J(θ),通过相应的算法来寻找最优参数。
2. 策略目标函数
强化学习的目标就是让个体在与环境交互过程中获得尽可能多的累计奖励,一个好的策略应该能准确反映强化学习的目标。
对于一个能够形成完整状态序列的交互环境来说,由于一个策略决定了个体与环境的交互,因而可以设计目标函数 J 1 ( θ ) J_1(\theta) J1(θ)为使用策略 π θ \pi_{\theta} πθ时 初始状态价值(start value) ,也就是初始状态收获的期望:
有些环境是没有明确的起始状态和终止状态,个体持续的与环境进行交互。在这种情况下可以使用 平均价值(average value) 或者 每一时间步的平均奖励(average reward per time-step) 来设计策略目标函数:
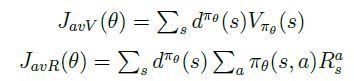
其中, d π θ ( s ) d^{\pi_{\theta}}(s) dπθ(s)是基于策略 π θ \pi_{\theta} πθ生成的马尔科夫链关于状态的平稳分布。
可以看到以上三种策略目标函数都与价值联系起来,价值越大,就说明策略越好,因此上述的函数应该采用梯度上升法来更新参数 θ \theta θ:

假设现在有一个单步马尔科夫决策过程,对应的强化学习问题是个体与环境每产生一个行为交互一次即得到一个即时奖励 r = R s , a r = R_{s,a} r=Rs,a,并形成一个完整的状态序列。根据前述的第三个策略目标函数,策略目标函数为:
对其求梯度:
上式中 ∇ θ log π θ ( s , a ) \nabla_{\theta} \log \pi_{\theta}(s, a) ∇θlogπθ(s,a)称为分值函数(score function)。
策略梯度定理:对于任何可微的 策略函数 π θ ( s , a ) \pi_{\theta}(s,a) πθ(s,a) 以及 三种策略目标函数 J = J 1 , J a v V , J a v R J= J_1,J_{avV},J_{avR} J=J1,JavV,JavR中的任意一种 来说,策略目标函数的梯度(策略梯度)都可以写成用 分值函数 表示的形式:
上式建立了 策略梯度 与 分值函数 以及 行为价值函数 之间的关系。
分值函数的在基于策略梯度的强化学习中有着很重要的意义。现通过两个常用的基于线性特征组合的策略来解释说明
-
Softmax 策略:
Softmax 策略是应用于 离散行为空间 的一种常用策略。该策略使用描述状态和行为的特征 ϕ ( s , a ) \phi(s,a) ϕ(s,a)与参数 θ \theta θ的线性组合来权衡一个行为发生的几率:
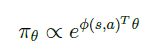
相应的分值函数为:

-
高斯策略
高斯策略是应用于 连续行为空间 的一种常用策略。该策略对应的行为从高斯分布 N ( μ ( s ) , σ 2 ) N(\mu(s),\sigma^2) N(μ(s),σ2)中产生。其均值 μ ( s ) = ϕ ( s ) T θ \mu(s)=\phi(s)^T\theta μ(s)=ϕ(s)Tθ。高斯策略对应的分值函数为:
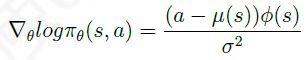
应用策略梯度可以比较容易得到 基于蒙特卡洛学习的策略梯度算法。该算法使用随机梯度上升来更新参数,同时使用某状态的收获 G t G_t Gt来作为基于策略 π θ \pi_{\theta} πθ下行为价值 Q π θ ( s t , a t ) Q_{\pi_{\theta}}(s_t, a_t) Qπθ(st,at)的无偏采样。参数更新方法为:
![]()
但是基于蒙特卡洛学习的策略梯度算法实际应用不多,主要是由于其需要完整的状态序列来计算收获,同时用收获来代替行为价值也存在较高的变异性,导致许多次的参数更新的方向有可能不是真正策略梯度的方向。
为了解决这一问题,提出了一种联合基于价值函数和策略函数的算法,这就是下文要介绍的Actor-Critic 算法。
3. Actor-Critic算法
Actor-Critic 算法的名字很形象,它包含一个 策略函数 和 行为价值函数,其中策略函数充当演员(Actor),生成行为与环境交互;行为价值函数充当评论家(Critic),负责评价演员的表现,并指导演员的后续行为动作。
Critic 的行为价值函数是基于策略 π θ \pi_{\theta} πθ的一个近似︰
![]()
Critic是一个神经网络,输入是状态和动作,输出是Q值(或者输入是状态,输出是状态价值V)。这个网络的训练是为了让它的预测结果尽可能地逼近真值。网络的预测值为 Q ( s , a ) Q(s,a) Q(s,a),网络的实际值用下一状态的 Q Q Q表示,即: r + γ Q ( s ′ , a ′ ) r+\gamma Q(s',a') r+γQ(s′,a′),两者进行作差,然后用一些常用的loss函数进行网络训练。
Actor也是一个神经网络,输入是状态,输出是离散动作的分布函数的关键参数(或者离散动作的概率)。这个网络的目标是如果这次被选中的动作获得了正的奖励,那么在下一次被选中的概率增大,如果这次被选中的动作获得了负的奖励,那么在下一次被选中的概率减小。Actor网络的参数 θ \theta θ的增量用下面的梯度公式进行计算:

最基本的基于行为价值Q的Actor-Critic算法流程如下所述:

因为在Critic 的行为价值函数中用神经网络进行了近似。所以在计算Actor网络的策略梯度时也是近似公式,即前述的:
![]()
那么什么时候能够严格地相等呢?
相容函数近似定理(Compatible Function Approximation Theorem) 说明了这个问题。定理的条件和结论如下:

实践过程中,使用 Q w ( s , a ) Q_w(s,a) Qw(s,a)来计算策略目标函数的梯度并不能保证每次都很幸运,有时候还会发生数据过大等异常情况。出现这类问题是由于 行为价值 本身有较大的 变异性。为了解决这个问题,提出了一个与行为无关仅基于状态的 基准 (baseline)函数B(s) 的概念,即要求B(s)满足:
当基准函数B(s)满足上述条件时,可以将其从策略梯度中提取出以减少变异性同时不改变其期望值,而基于状态的价值函数 V π θ ( s ) V_{\pi_{\theta}}(s) Vπθ(s)函数就是一个不错的基准函数。令优势函数(advantagefunction)为:
4. 深度确定性策略梯度(DDPG)算法
深度确定性策略梯度算法是使用深度学习技术、同时基于Actor-Critic算法的确定性策略算法。该算法中的 Actor 和Critic都使用深度神经网络来建立近似函数。
由于该算法可以直接从Actor 的策略生成确定的行为而不需要依据行为的概率分布进行采样而被称为确定性策略。
该算法在学习阶段通过在确定性的行为基础上增加一个噪声函数而实现在确定性行为周围的小范围内探索。此外,该算法还为Actor 和Critic网络各备份了一套参数用来计算行为价值的期待值以更稳定地提升Critic的策略指导水平。使用备份参数的网络称为 目标网络,其对应的参数 每次更新的幅度很小(又称软更新)。另一套参数对应的Actor 和Critic则用来生成实际交互的行为以及计算相应的策略梯度,这一套参数 每学习一次就更新一次。这种双参数设置的目的是为了减少因近似数据的引导而发生不收敛的情形。这四个网络具体使用的情景为:
-
Actor 网络:根据当前状态 s 0 s_0 s0生成的探索或不探索的具体行为 a 0 a_0 a0;
-
Target Actor网络︰根据环境给出的后续状态 s 1 s_1 s1生成预估价值用到的 a 1 a_1 a1;
-
Critic网络:计算状态 s 0 s_0 s0和生成的行为 a 0 a_0 a0对应的行为价值;
-
Target Critic网络:根据后续状态 s 1 , a 1 s_1,a_1 s1,a1生成用来计算目标价值 y = Q ( s 0 , a 0 ) y =Q(s_0, a_0) y=Q(s0,a0)的 Q ′ ( s 1 , a 1 ) Q'(s_1, a_1) Q′(s1,a1);
DDPG算法表现出色,能较为稳定地解决连续行为空间下强化学习问题,其具体流程如下图所示:
更通俗易懂的讲解可以看: 强化学习番外(1)——图解DQN,DDQN,DDPG网络.
5. 编程实践
本章的编程实践是《DDPG算法实现》,用DDPG算法完成puckworld小游戏,详见叶强github强化学习主页。
参考文献:
- David Silver强化学习视频.
- 叶强《强化学习入门——从原理到实践》