基于互补格雷码的三维面结构光测量
High-speed three-dimensional shape measurement based on cyclic complementary Gray-code light–基于循环互补格雷码的高速三维形貌测量
- 作者：吴周杰，张启灿等
- 期刊：Optics and Lasers in Engineering，2012
研究内容
本文作者提出一种基于互补格雷码的相移相位展开方法，可用于高速三维重建工作。
我主要是学习基于格雷码相位展开技术，所以，本文的基于格雷码的高速三维测量部分我没深入看，感兴趣的可以自己下载文献看看。
论文创新点
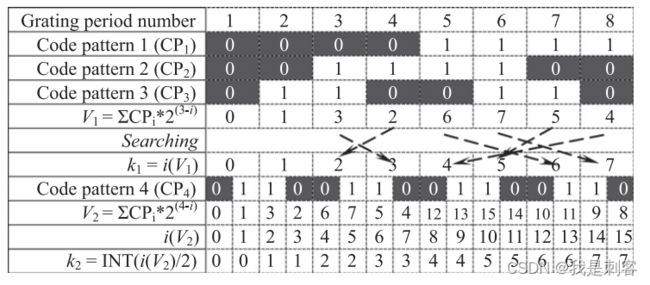
传统格雷码辅助展开相移相位时，总是在二值化的格雷码边界有1，2个像素解码错误（这是不可避免的，因为投影仪与相机分辨率不匹配，相机离焦等原因），本文作者提出互补格雷码辅助展开相位，即在传统格雷码图案上多投影一幅格雷码图案，使用N+1位格雷码编码来辅助解码相位，避免了展开的连续相位在截断相位处因格雷码边界解码错误导致的尖峰错误。本文提出的方法对不连续的物体相位也可以正确的展开。
实验方法
基本思想
格雷码辅助展开相位的基本思路就是格雷码最小周期与条纹图的周期一致，这样格雷码总是在截断相位处发生级次改变，从而把截断相位展开位连续相位，如下图所示。然而在实际解码过程中，格雷码级次跳变的地方不一定恰好与截断相位的周期完全重合。
实验方法
-
生成 N + 1 N+1 N+1位格雷码图案，以及相移图案，其中，相移条纹周期与 N N N位格雷码最小周期相同，比如投影仪宽度位1024，假设使用4+1位格雷码图案，则4位格雷码图案最小周期位 1024 2 4 = 64 \frac{1024}{2^4}=64 241024=64个像素，则条纹周期 T = 64 T = 64 T=64。 N N N位格雷码图案用于求解级次 k 1 k_1 k1， N + 1 N+1 N+1位格雷码图案用于求解级次 k 2 k_2 k2。
-
- 互补格雷码解码过程如图2所示，其中， k 2 = ⌊ i ( V 2 ) + 1 2 ⌋ k_2=\lfloor \frac{i(V_2) + 1}{2} \rfloor k2=⌊2i(V2)+1⌋
- 互补格雷码解码过程如图2所示，其中， k 2 = ⌊ i ( V 2 ) + 1 2 ⌋ k_2=\lfloor \frac{i(V_2) + 1}{2} \rfloor k2=⌊2i(V2)+1⌋
-
相位展开过程如下公式所示：
Φ ( x , y ) = { ϕ ( x , y ) + 2 π k 2 , ϕ ( x , y ) ≤ π / 2 ϕ ( x , y ) + 2 π k 1 , π / 2 < ϕ ( x , y ) ≤ 3 π / 2 ϕ ( x , y ) + 2 k 2 π − 2 π , 3 π / 2 ≤ ϕ ( x , y ) (1) \Phi(x,y)=\begin{cases} \phi(x,y) + 2 \pi k_2, & \quad {\phi(x,y)\leq\pi / 2}\\ \phi(x,y) + 2 \pi k_1, & \quad {\pi/2 < \phi(x,y) \leq 3\pi/2}\\ \phi(x,y)+2k_2\pi-2\pi, &\quad {3\pi/2 \leq \phi(x,y)} \end{cases} \tag{1} Φ(x,y)=⎩⎪⎨⎪⎧ϕ(x,y)+2πk2,ϕ(x,y)+2πk1,ϕ(x,y)+2k2π−2π,ϕ(x,y)≤π/2π/2<ϕ(x,y)≤3π/23π/2≤ϕ(x,y)(1)
其中， ϕ \phi ϕ是截断相位， Φ \Phi Φ是展开后的连续相位。在实际处理时，截断相位被截断在 [ − π , π ) [-\pi,\pi) [−π,π)之间，要把它映射到 [ 0 , 2 π ) [0,2\pi) [0,2π)之间，然后使用公式(1)进行相位展开。
结论
相位展开的过程实际上就是通过在截断相位处加减 2 k π 2k\pi 2kπ把截断相位拉直的过程，格雷码辅助相位展开就是通过格雷码来求解截断相位级次。本文提出的互补格雷码方式避免了因待测物体复杂导致格雷码二值化过程中总会在边界处产生1，2个像素级次错位而引起的相位跳变的问题，有效避免了相位展开错误。互补格雷码辅助相位展开关键在于格雷码二值化是否有误，针对平滑的物体，可能二值化不会出现问题，但是对于特别复杂的待测物体，比如拥有大量引脚的CPU插座，如果某个像素二值化错误，则导致该像素相位，后续可能还需要做相应的滤波平滑展开的相位。
补充材料
-
格雷码：格雷码编码及解码参考网页
-
代码：基于论文实现的MATLAB代码下载