交叉熵在深度学习中的实践应用
交叉熵在深度学习中的实践应用
flyfish
理论说明
一张图说明Multi-Class 分类 和Multi-Label 分类的区别
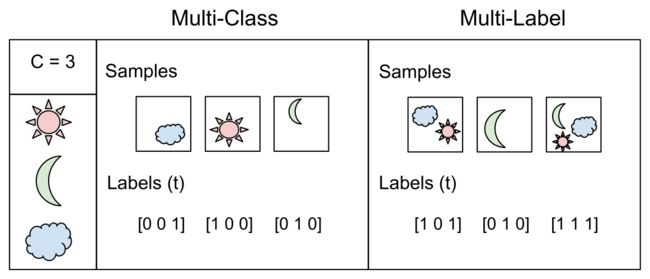
假设一共有C类,这样一共有3类,一张图里只有一个目标,表示label的向量里只有一个1
这是Multi-Class,正类(positive class) 只有一个, 有C−1个负类( negative classes)
假设一共有3类,一张图里有多个目标,表示label的向量里有多个1,也就是正类(positive class)可以有多个
这是Multi-Label。
代码里通常用target 表示ground truth,也就是图片中标签(label)的表示,用target 向量存储这些标签(label)
target 向量中的类别索引对应的值为1,就表示图片中有该类目标
太阳、月亮、云 ,索引分别是0、1、2
如果label是1、0、0表示 有太阳(类别索引0的位置为1)
如果label是0、1、0表示 有月亮(类别索引1的位置为1)
CrossEntropyLoss的两个重要参数
Input: (N,C) C 是类别的数量,N是mini-batch的大小,内容是每个类的得分
Target: (N) N是mini-batch的大小,0 <= targets[i] <= C-1
#存储的是索引 假设一共有3类,如果Target是2 表示one-hot向量 001,Target是1表示010
下面的代码是以Multi-Class分类的交叉熵来描述
假设有这样的数据
target可以换成label,ground truth等,one hot 向量表示
| input(predicted values) | target(Ground truth values) |
|---|---|
| 1 、2、 7 | 0、0、1 |
交叉熵损失(Cross-Entropy loss)通常定义
公式里的log对应的是以e为底,这里没有使用数学里的ln,对应的函数通常是exp
Loss = − ∑ i = 1 N y ^ i ∗ log ( y i ) \operatorname{Loss}=-\sum_{i=1}^{N} \hat{y}_{i} * \log \left(y_{i}\right) Loss=−i=1∑Ny^i∗log(yi)
y ^ i \hat{y}_{i} y^i是ground truth的值(Ground truth values),是打标签(label)的值,是one-hot向量,代码常用一个叫做Target 向量存储这些值
定义下数据
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
input = torch.tensor([[1, 2, 7]]).float()
target = torch.tensor([2]).long()# 001
一 、 C r o s s E n t r o p y L o s s 一 、CrossEntropyLoss 一、CrossEntropyLoss API实现
可以用直接用CrossEntropyLoss API实现
loss = nn.CrossEntropyLoss() output = loss(input, target)
print(output)#tensor(0.0092)
CrossEntropyLoss的两个重要参数
Input: (N,C) C 是类别的数量,N是mini-batch的大小,内容是每个类的得分
Target: (N) N是mini-batch的大小,0 <= targets[i] <= C-1
存储的是索引 假设一共有3类,如果Target是2 表示one-hot向量 001,Target是1表示010
二、 L o g S o f t m a x + N L L L o s s LogSoftmax+NLLLoss LogSoftmax+NLLLoss实现
y i y_{i} yi是预测值(predicted values),也就是softmax的结果
我先计算下softmax,按照惯例我会列举softmax多种写法,然后找出你最熟悉的字母
S ( f y i ) = e f y i ∑ j e f j S(f_{y_i}) = \dfrac{e^{f_{y_i}}}{\sum_{j}e^{f_j}} S(fyi)=∑jefjefyi
s o f t m a x ( x j ) = e x j ∑ i = 1 n e x i softmax(x_j)=\frac{e^{x_j}}{\sum_{i=1}^{n} e^{x_i}} softmax(xj)=∑i=1nexiexj
s ( x i ) = e x i ∑ j = 1 n e x j s\left(x_{i}\right)=\frac{e^{x_{i}}}{\sum_{j=1}^{n} e^{x_{j}}} s(xi)=∑j=1nexjexi
Softmax ( x i ) = exp ( x i ) ∑ j exp ( x j ) \operatorname{Softmax}\left(x_{i}\right)=\frac{\exp \left(x_{i}\right)}{\sum_{j} \exp \left(x_{j}\right)} Softmax(xi)=∑jexp(xj)exp(xi)
softmax ( z j ) = e z j ∑ k = 1 K e z k for j = 1 , … , K \operatorname{softmax}\left(z_{j}\right)=\frac{e^{z_{j}}}{\sum_{k=1}^{K} e^{z_{k}}} \text { for } j=1, \ldots, \mathrm{K} softmax(zj)=∑k=1Kezkezj for j=1,…,K
把公式拆解
假设有4个数分别是 z 1 , z 2 , z 3 , z 4 z_1 ,z_2,z_3,z_4 z1,z2,z3,z4我们计算其中一个 z 1 z_1 z1
softmax ( z 1 ) = e z 1 ∑ k = 1 K e z k for j = 1 , … , K = e z 1 e z 1 + e z 2 + e z 3 + e z 4 \begin{aligned} \operatorname{softmax}\left(z_{1}\right) &=\frac{e^{z_{1}}}{\sum_{k=1}^{K} e^{z_{k}}} \text { for } j=1, \ldots, \mathrm{K} \\ &=\frac{e^{z_{1}}}{e^{z_{1}}+e^{z_{2}}+e^{z_{3}}+e^{z_{4}}} \\ \end{aligned} softmax(z1)=∑k=1Kezkez1 for j=1,…,K=ez1+ez2+ez3+ez4ez1
输出结果都加起来和是1
e z 1 e z 1 + e z 2 + e z 3 + e z 4 + e z 2 e z 1 + e z 2 + e z 3 + e z 4 + e z 3 e z 1 + e z 2 + e z 3 + e z 4 + e z 4 e z 1 + e z 2 + e z 3 + e z 4 = e z 1 + e z 2 + e z 3 + e z 4 e z 1 + e z 2 + e z 3 + e z 4 = 1 \begin{array}{l} \frac{e^{z_{1}}}{e^{z_{1}}+e^{z_{2}}+e^{z_{3}}+e^{z_{4}}}\\ +\frac{e^{z_{2}}}{e^{z_{1}}+e^{z_{2}}+e^{z_{3}}+e^{z_{4}}} \\ +\frac{e^{z_{3}}}{e^{z_{1}}+e^{z_{2}}+e^{z_{3}}+e^{z_{4}}}\\ +\frac{e^{z_{4}}}{e^{z_{1}}+e^{z_{2}}+e^{z_{3}}+e^{z_{4}}} \\ \\ =\frac{e^{z_{1}}+e^{z_{2}}+e^{z_{3}}+e^{z_{4}}}{e^{z_{1}}+e^{z_{2}}+e^{z_{3}}+e^{z_{4}}}=1 \end{array} ez1+ez2+ez3+ez4ez1+ez1+ez2+ez3+ez4ez2+ez1+ez2+ez3+ez4ez3+ez1+ez2+ez3+ez4ez4=ez1+ez2+ez3+ez4ez1+ez2+ez3+ez4=1
那么代码就是这样
def softmax1(x):
result = np.exp(x) / np.sum(np.exp(x), axis=0)
return result
问题就出现了 e的n次方 ,
n比较大时容易溢出结果是[nan nan nan]
n比较小时例如 -100000,结果是invalid value encountered in true_divide
所以还需要改进公式
为了使softmax函数在数值上稳定,需要将向量中的值标准化,方法是将分子和分母乘以一个常数
过程证明如下
s o f t m a x ( z j ) = e z j ∑ k = 1 N e z k = C e z j C ∑ k = 1 N e z k = e z j + log ( C ) ∑ k = 1 N e z k + log ( C ) \begin{aligned} {softmax}\left(z_{j}\right) &=\frac{e^{z_{j}}}{\sum_{k=1}^{N} e^{z_{k}}} \\ \\ &=\frac{C e^{z_{j}}}{C \sum_{k=1}^{N} e^{z_{k}}} \\ \\ &=\frac{e^{z_{j}+\log (C)}}{\sum_{k=1}^{N} e^{z_{k}+\log (C)}} \end{aligned} softmax(zj)=∑k=1Nezkezj=C∑k=1NezkCezj=∑k=1Nezk+log(C)ezj+log(C)
l o g ( C ) 的 值 为 − m a x ( z ) log(C)的值为−max(z) log(C)的值为−max(z),所以代码就变成了下面的样子
def softmax2(X):
result = np.exp(X - np.max(X))
return result / np.sum(result,axis=0)
softmax计算完再计算logsoftmax
log(Softmax(x))
PyTorch官网将式子拆开是 以下字母将采用PyTorch官网使用的字母
log Softmax ( x i ) = log ( exp ( x i ) ∑ j exp ( x j ) ) \log \operatorname{Softmax}\left(x_{i}\right)=\log \left(\frac{\exp \left(x_{i}\right)}{\sum_{j} \exp \left(x_{j}\right)}\right) logSoftmax(xi)=log(∑jexp(xj)exp(xi))
所以代码可以是这样(多写一份numpy版)
Intermediate1=np.log(softmax2(scores))
Intermediate2=torch.log(torch.tensor(softmax2(scores)))
print("Intermediate1:",Intermediate1)#[-6.00917448 -5.00917448 -0.00917448] 如果末尾保留4为小数,则与tensor数据一致
print("Intermediate2:",Intermediate2)#tensor([-6.0092, -5.0092, -0.0092], dtype=torch.float64)
loss = nn.NLLLoss()
output = loss(Intermediate2.view(1,3), target)
print(output)#tensor(0.0092)
如果是自带的LogSoftmax API实现可以这样写
ls = nn.LogSoftmax(dim=1)
Intermediate = ls(input)
print("Intermediate:",Intermediate)
#Intermediate: tensor([[-6.0092, -5.0092, -0.0092]])
loss = nn.NLLLoss()
output = loss(Intermediate, target)
print(output)#tensor(0.0092)
NLLLoss是negative log likelihood loss缩写 ,计算方法如下
在这个例子中, target是2, one-hot表示为(0,0,1), NLLLoss的计算如下
− ( 0 ∗ ( − 6.0092 ) + 0 ∗ ( − 5.0092 ) + 1 ∗ ( − 0.0092 ) ) = 0.0092 -(0* (-6.0092)+0*(-5.0092)+1*(-0.0092))=0.0092 −(0∗(−6.0092)+0∗(−5.0092)+1∗(−0.0092))=0.0092
最终结果是0.0092
三、logSumExp实现
关于logsoftmax的变形
log ( e x j ∑ i = 1 n e x i ) = log ( e x j ) − log ( ∑ i = 1 n e x i ) = x j − log ( ∑ i = 1 n e x i ) \begin{aligned} \log \left(\frac{e^{x} j}{\sum_{i=1}^{n} e^{x_{i}}}\right) &=\log \left(e^{x_{j}}\right)-\log \left(\sum_{i=1}^{n} e^{x_{i}}\right) \\ &=x_{j}-\log \left(\sum_{i=1}^{n} e^{x_{i}}\right) \end{aligned} log(∑i=1nexiexj)=log(exj)−log(i=1∑nexi)=xj−log(i=1∑nexi)
因为
log SumExp ( x 1 … x n ) = log ( ∑ i = 1 n e x i ) \log \operatorname{SumExp}\left(x_{1} \ldots x_{n}\right)=\log \left(\sum_{i=1}^{n} e^{x_{i}}\right) logSumExp(x1…xn)=log(i=1∑nexi)
代码编写的依据是
log ( Softmax ( x j , x 1 … x n ) ) = x j − log SumExp ( x 1 … x n ) = x j − ( log ( ∑ i = 1 n e x i − c ) + c ) \begin{aligned} \log \left(\text {Softmax}\left(x_{j}, x_{1} \ldots x_{n}\right)\right) &=x_{j}-\log \operatorname{SumExp}\left(x_{1} \ldots x_{n}\right) \\ &=x_{j}-(\log \left(\sum_{i=1}^{n} e^{x_{i}-c}\right)+c) \end{aligned} log(Softmax(xj,x1…xn))=xj−logSumExp(x1…xn)=xj−(log(i=1∑nexi−c)+c)
logSumExp中间过程是
根据对数运算法则
e a ⋅ e b = e a + b log ( a ⋅ b ) = log ( a ) + log ( b ) log SumExp ( x 1 … x n ) = log ( ∑ i = 1 n e x i ) = log ( ∑ i = 1 n e x i − c e c ) = log ( e c ∑ i = 1 n e x i − c ) = log ( ∑ i = 1 n e x i − c ) + log ( e c ) = log ( ∑ i = 1 n e x i − c ) + c \begin{aligned} e^{a} \cdot e^{b}&=e^{a+b} & \\ \log (a \cdot b) &=\log (a)+\log (b) \\ \\ \log \operatorname{SumExp}\left(x_{1} \ldots x_{n}\right) &=\log \left(\sum_{i=1}^{n} e^{x_{i}}\right) \\ &=\log \left(\sum_{i=1}^{n} e^{x_{i} - c} e^{c}\right) \\ &=\log \left(e^{c} \sum_{i=1}^{n} e^{x_{i}- c}\right) \\ &=\log \left(\sum_{i=1}^{n} e^{x_{i}- c}\right)+\log \left(e^{c}\right) \\ &=\log \left(\sum_{i=1}^{n} e^{x_{i}- c}\right)+c \end{aligned} ea⋅eblog(a⋅b)logSumExp(x1…xn)=ea+b=log(a)+log(b)=log(i=1∑nexi)=log(i=1∑nexi−cec)=log(eci=1∑nexi−c)=log(i=1∑nexi−c)+log(ec)=log(i=1∑nexi−c)+c
换成另一种方式
y = log SumExp ( x 1 … x n ) y=\log \operatorname{SumExp}\left(x_{1} \ldots x_{n}\right) y=logSumExp(x1…xn)
y = log ∑ i = 1 n e x i e y = ∑ i = 1 n e x i e − c e y = e − c ∑ i = 1 n e x i e y − c = ∑ i = 1 n e − c e x i y − c = log ∑ i = 1 n e x i − c y = log ∑ i = 1 n e x i − c + c \begin{aligned} y &=\log \sum_{i=1}^{n} e^{x_{i}} \\ e^{y} &=\sum_{i=1}^{n} e^{x_{i}} \\ e^{-c} e^{y} &=e^{-c} \sum_{i=1}^{n} e^{x_{i}} \\ e^{y-c}&=\sum_{i=1}^{n} e^{-c} e^{x_{i}} \\ y-c&=\log \sum_{i=1}^{n} e^{x_{i}-c} \\ y&=\log \sum_{i=1}^{n} e^{x_{i}-c}+c \end{aligned} yeye−ceyey−cy−cy=logi=1∑nexi=i=1∑nexi=e−ci=1∑nexi=i=1∑ne−cexi=logi=1∑nexi−c=logi=1∑nexi−c+c
C的取值
c = max i x i c=\max _{i} x_{i} c=imaxxi
那么代码可以这样写
c=input.max(dim=1,keepdim=True)
d=torch.logsumexp(input, 1,keepdim=True)
Intermediate=input-d
print(Intermediate)#tensor([[-6.0092, -5.0092, -0.0092]]) 与上面的值完全相同
loss = nn.NLLLoss()
output = loss(Intermediate, target)
print(output)#tensor(0.0092)
如果把torch.logsumexp拆开可以这样写
c = input.data.max()
d=(torch.log(torch.sum(torch.exp(input - c), 1, keepdim=True)) + c)
Intermediate=input-d
print(Intermediate)#tensor([[-6.0092, -5.0092, -0.0092]]) 与上面的值完全相同
loss = nn.NLLLoss()
output = loss(Intermediate, target)
print(output)#tensor(0.0092)
完整的源码如下
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
input = torch.tensor([[1, 2, 7]]).float()
target = torch.tensor([2]).long()# 001
#-----------------------------------------------------
# 方法1
loss = nn.CrossEntropyLoss()
output = loss(input, target)
print(output)#tensor(0.0092)
#-----------------------------------------------------
# 方法2
ls = nn.LogSoftmax(dim=1)
Intermediate = ls(input)
print("Intermediate:",Intermediate)
#Intermediate: tensor([[-6.0092, -5.0092, -0.0092]])
loss = nn.NLLLoss()
output = loss(Intermediate, target)
print(output)#tensor(0.0092)
#-----------------------------------------------------
# 方法3
scores = np.array([1, 2, 7])
def softmax1(x):
result = np.exp(x) / np.sum(np.exp(x), axis=0)
return result
def softmax2(X):
result = np.exp(X - np.max(X))
return result / np.sum(result,axis=0)
print(softmax1(scores))#[0.00245611 0.00667641 0.99086747]
print(softmax2(scores))#[0.00245611 0.00667641 0.99086747]
Intermediate1=np.log(softmax2(scores))
Intermediate2=torch.log(torch.tensor(softmax2(scores)))
print("Intermediate1:",Intermediate1)#[-6.00917448 -5.00917448 -0.00917448] 如果末尾保留4为小数,则与tensor数据一致
print("Intermediate2:",Intermediate2)#tensor([-6.0092, -5.0092, -0.0092], dtype=torch.float64)
loss = nn.NLLLoss()
output = loss(Intermediate2.view(1,3), target)
print(output)#tensor(0.0092)
#一个np类型,一个tensor类型
#输出与上面的Intermediate一致,可以再执行NLLLoss
#主要用于区别softmax2比softmax1更稳定
#-----------------------------------------------------
#方法4
c=input.max(dim=1,keepdim=True)
d=torch.logsumexp(input, 1,keepdim=True)
Intermediate=input-d
print(Intermediate)#tensor([[-6.0092, -5.0092, -0.0092]]) 与上面的值完全相同
loss = nn.NLLLoss()
output = loss(Intermediate, target)
print(output)#tensor(0.0092)
#-----------------------------------------------------
#方法5
c = input.data.max()
d=(torch.log(torch.sum(torch.exp(input - c), 1, keepdim=True)) + c)
Intermediate=input-d
print(Intermediate)#tensor([[-6.0092, -5.0092, -0.0092]]) 与上面的值完全相同
loss = nn.NLLLoss()
output = loss(Intermediate, target)
print(output)#tensor(0.0092)
#-----------------------------------------------------
关于 torch.nn.CrossEntropyLoss的参数
版本 PyTorch 1.5
参数size_average,reduce都是要被废弃的,所以重点是reduction
一共有3个值可以选择 none’ | ‘mean’ | ‘sum’
当batchsize=1时
input = torch.tensor([[1, 2, 7]]).float()
target = torch.tensor([2]).long()# 001
none’ | ‘mean’ | ‘sum’
输出分别是
tensor(0.0092)
tensor([0.0092])
tensor(0.0092)
tensor(0.0092)
没有变化
假设batchsize=3,
3个样本的时候
import torch
import torch.nn as nn
#3个样本
input = torch.tensor([[1, 2, 7],[4,7,9],[8,3,4]]).float()
target = torch.tensor([2,2,0]).long()# 001
loss = nn.CrossEntropyLoss()
loss1 = nn.CrossEntropyLoss(reduction="none")
loss2 = nn.CrossEntropyLoss(reduction="mean")
loss3 = nn.CrossEntropyLoss(reduction="sum")
output = loss(input, target)
output1 = loss1(input, target)
output2 = loss2(input, target)
output3 = loss3(input, target)
print(output)
print(output1)
print(output2)
print(output3)
# tensor(0.0556)
# tensor([0.0092, 0.1328, 0.0247])#none
# tensor(0.0556)#mean
# tensor(0.1668)#sum
默认情况reduction=“mean”
mean表示 均值 0.1668 / 3= 0.0556
sum表示和 0.0092 + 0.1328 + 0.0247 =0.1668
参考
关于论文
tricks-of-the-trade-logsumexp
Understanding Categorical Cross-Entropy Loss, Binary Cross-Entropy Loss, Softmax Loss, Logistic Loss, Focal Loss and all those confusing names
Classification and Loss Evaluation - Softmax and Cross Entropy Loss
The log-sum-exp trick in Machine Learning
torch.nn.CrossEntropyLoss
torch.nn.LogSoftmax
Understanding softmax and the negative log-likelihood