小曾带你刷leetcode--二分查找篇
文章目录
-
- 前言
- 二分查找简介
-
- 二分查找框架
- 寻找一个数(基于二分搜索)
- 寻找左侧边界的二分搜索
- 寻找右侧边界的二分查找
- 总结
-
- 4. 寻找两个正序数组的中位数
- 33. 搜索旋转排序数组
- 34. 在排序数组中查找元素的第一个和最后一个位置
- 35. 搜索插入位置
- 81. 搜索旋转排序数组 II
前言

leetcode 刷题,贵在坚持,不积跬步,无以至千里,不积小流,无以成江海。有了坚持和正确的方向,干就完了。

leetcode正确的刷题方式:是按照上图中知识点来逐渐击破,在每一个专题中掌握主要思想以及解题技巧,由点到面,不断扩大自己的知识库。
下面小曾就带着大家刷力扣–二分查找篇
二分查找简介
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
要求:顺序存储结构、有序排列
下面首先给大家介绍一个笑话来理解一下二分查找思想:
有⼀天小曾到图书馆借了 N 本书,出图书馆的时候,警报响了,于是保安
把小曾拦下,要检查⼀下哪本书没有登记出借。小曾正准备把每⼀本书在报
警器下过⼀下,以找出引发警报的书,但是保安露出不屑的眼神:你连⼆分
查找都不会吗?于是保安把书分成两堆,让第⼀堆过⼀下报警器,报警器
响;于是再把这堆书分成两堆…… 最终,检测了 logN 次之后,保安成功的
找到了那本引起警报的书,露出了得意和嘲讽的笑容。于是小曾背着剩下的
书⾛了。
从此,图书馆丢了 N - 1 本书。
对于我身边同学而言,他们都觉得二分查找比较简单,事实真的如此吗?
Knuth 大佬(发明 KMP 算法的那位)就说二分查找 思路很简单,细节是魔鬼。
下面我们主要来探究几个最常用的二分查找场景:寻找一个数、寻找左侧边界、寻找右侧边界。
对于一些细节问题,有while循环中的不等号是否应该带等号,mid 是否应该加一等等。我们要了解这些细节之间的差异,细节决定成败,这有所获。
二分查找框架
掌握框架,根据问题进行套用即可,大致框架如下:
int binarySearch(int[] nums, int target) {
int left = 0, right = ...; [1]
while(... [2]) {
int mid = (right + left) / 2;
if (nums[mid] == target) {
...[3]
} else if (nums[mid] < target) {
left = ...[4]
} else if (nums[mid] > target) {
right = ...[5]
}
}
return ...[6];
}
下面要特意强调的是:不要出现 else,而是把所有情况用 else if 写清楚,这样可以清楚地展现所有细节
对于标出…的地方根据不同的问题,[1-6]进行不同的填写,是展示问题细节的地方,所以根据问题,主要还是注意…这几块,来进行实例分析。
tips:计算 mid 时需要技巧防止溢出,建议写成: mid = left + (right - left) / 2
分析可知 left + (right - left) / 2 == (left+right)/2 ,前一种做法可以防止 left 和right 太大直接相加导致溢出。
下面介绍几个二分查找常见问题
寻找一个数(基于二分搜索)
对于二分查找这是比较常见,也是必备的,搜索一个数,如果存在,返回其索引,不存在则返回-1。
int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) { // 注意
int mid = (right + left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}
可以看出主要是在二分查找的框架上进行添加对应问题内容,如果存在,返回mid ,不存在,返回-1.
注意1、为什么 while 循环的条件中是 <=,⽽不是 <?
因为初始化 right 的赋值是 nums.length - 1,即最后一个元素的索引,而不是 nums.length
对于<= 而言 ,两端都为闭区间[left , right]
对于< 而言,两端为前闭后开[left , right) // 索引大小为num.length ,这时已经越界
对于索引在最右端,即 right = nums.length -1 ,使用是左右两端闭合区间【搜索区间:每次进行搜索的区间】
注意2、while语句是判断什么时候进行停止搜索?
1、找到目标值,则停止搜索
if(nums[mid] == target)
return mid;
2、搜索从左向右全部搜索完,还没有找到目标值,即终止
换句话说,搜索空间为空,即终止
while(left <= right) 终止条件是 left == right + 1,写成区间的形式就是 [right + 1, right],或者带个具体的数字进去 [3, 2],可见这时候搜索区间为空,因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的,直接返回 -1 即可。
while(left < right)的终止条件是 left == right,写成区间的形式就是 [right, right],或者带个具体的数字进去 [2, 2],这时候搜索区间非空,还有一个数 2,但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了,索引 2 没有被搜索,如果这时候直接返回 -1 就可能出现错误。
还有一种补救方法:用 while(left < right) 也可以
while(left < right) {
// ...
}
return nums[left] == target ? left : -1;
注意3、为什么 left = mid + 1,right = mid - 1?我看有的代码是 right = mid 或者 left = mid,没有这些加加减减,到底怎么回事,怎么判断?
这也是二分查找的一个难点,不过只要你能理解前面的内容,就能够很容易判断。
刚才明确了「搜索区间」这个概念,而且本算法的搜索区间是两端都闭的,即 [left, right]。那么当我们发现索引 mid 不是要找的 target 时,如何确定下一步的搜索区间呢?
当然是去搜索 [left, mid - 1] 或者 [mid + 1, right] 对不对?因为 mid 已经搜索过,应该从搜索区间中去除。
注意4、此算法有什么缺陷?
答:至此,你应该已经掌握了该算法的所有细节,以及这样处理的原因。但是,这个算法存在局限性。
比如说给你有序数组 nums = [1,2,2,2,3],target = 2,此算法返回的索引是 2,没错。但是如果我想得到 target 的左侧边界,即索引 1,或者我想得到 target 的右侧边界,即索引 3,这样的话此算法是无法处理的。
这样的需求很常见。你也许会说,找到一个 target 索引,然后向左或向右线性搜索不行吗?可以,但是不好,因为这样难以保证二分查找对数级的时间复杂度了。
我们后续的算法就来讨论这两种二分查找的算法。
寻找左侧边界的二分搜索
具体代码:
int left_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0;
int right = nums.length; // 注意
while (left < right) { // 注意
int mid = (left + right) / 2;
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid; // 注意
}
}
return left;
}
注意1:为什么 while(left < right) 而不是 <= ?
答:用相同的方法分析,因为初始化 right = nums.length 而不是 nums.length - 1 。因此每次循环的「搜索区间」是 [left, right) 左闭右开。
while(left < right) 终止的条件是 left == right,此时搜索区间 [left, left) 恰巧为空,所以可以正确终止。
其实有一个小技巧: 注意2、为什么没有返回 -1 的操作?如果 nums 中不存在 target 这个值,怎么办? 答:因为要一步一步来,先理解一下这个「左侧边界」有什么特殊含义: 比如对于有序数组 nums = [2,3,5,7], target = 1,算法会返回 0,含义是:nums 中小于 1 的元素有 0 个。如果 target = 8,算法会返回 4,含义是:nums 中小于 8 的元素有 4 个。 综上可以看出,函数的返回值(即 left 变量的值)取值区间是闭区间 [0, nums.length],所以我们简单添加两行代码就能在正确的时候 return -1: 注意3、为什么 left = mid + 1,right = mid ?和之前的算法不一样? 答:这个很好解释,因为我们的「搜索区间」是 [left, right) 左闭右开,所以当 nums[mid] 被检测之后,下一步的搜索区间应该去掉 mid 分割成两个区间,即 [left, mid) 或 [mid + 1, right)。 注意4、为什么该算法能够搜索左侧边界? 答:关键在于对于 nums[mid] == target 这种情况的处理: 可见,找到 target 时不要立即返回,而是缩小「搜索区间」的上界 right,在区间 [left, mid) 中继续搜索,即不断向左收缩,达到锁定左侧边界的目的。 注意5、为什么返回 left 而不是 right? 答:返回left和right都是一样的,因为 while 终止的条件是 left == right 注意6、能不能想办法把right变成nums.length-1,也就是继续使用两边都闭的「搜索区间」?这样就可以和第⼀种⼆分搜索在某种程度上统⼀起来了。 前提是理解【搜索空间】的概念,就能有效避免漏掉元素。 根据上述技巧中,需要将初始化right = nums.length-1 ,while判断就是left<=right , left == right+1,搜索空间[left , right]. 搜索空间[left , right],下面就是left 和 right 更新 由于 while 的退出条件是 left == right + 1 ,所以当 target ⽐ nums 中 完整代码: 寻找右侧边界和寻找左侧边界的代码差不多,只有两处不同,已标注: 注意1、为什么这个算法能够找到右侧边界? 答:类似地,关键点还是这里: 当 nums[mid] == target 时,不要立即返回,而是增大「搜索区间」的下界 left,使得区间不断向右收缩,达到锁定右侧边界的目的。 注意2、为什么最后返回 left - 1 而不像左侧边界的函数,返回 left?而且我觉得这里既然是搜索右侧边界,应该返回 right 才对。 答:首先,while 循环的终止条件是 left == right,所以 left 和 right 是一样的,你非要体现右侧的特点,返回 right - 1 好了。 至于为什么要减一,这是搜索右侧边界的一个特殊点,关键在这个条件判断: 因为我们对 left 的更新必须是 left = mid + 1,就是说 while 循环结束时,nums[left] 一定不等于 target 了,而 nums[left - 1]可能是target。 至于为什么 left 的更新必须是 left = mid + 1,同左侧边界搜索,就不再赘述。 注意3、为什么没有返回 -1 的操作?如果 nums 中不存在 target 这个值,怎么办? 答:类似之前的左侧边界搜索,因为 while 的终止条件是 left == right,就是说 left 的取值范围是 [0, nums.length],所以可以添加两行代码,正确地返回 -1: 注意4、是否也可以把这个算法的「搜索区间」也统⼀成两端都闭的形式呢?这 类似左侧边界统一写法,需要改的地方就两个地方 下面带大家梳理一下: 最基本的二分查找算法,返回索引 寻找左侧的二分查找,要找到左侧边界 寻找右侧的二分查找,要找到右侧边界 找到target 右侧索引 当nums[mid] ==target 的时候不要返回,而是缩小左侧边界用来锁定右侧边界 ⼜因为收紧左侧边界时必须 left = mid + 1 所以最后⽆论返回left还是right,必须减⼀ 整理以上三种写法,统一初始化,便于记忆 最后再具体就介绍一下重要内容 1、分析⼆分查找代码时,不要出现else,全部展开成else if方便理解。 2、注意「搜索区间」和 while 的终⽌条件,如果存在漏掉的元素,记得在最后检查。 3、如需定义左闭右开的「搜索区间」搜索左右边界,只要在nums[mid]== target 时做修改即可,搜索右侧时需要减⼀。 4、如果将「搜索区间」全都统⼀成两端都闭,好记,只要稍改 nums[mid]== target 条件处的代码和返回的逻辑即可。 掌握这些内容,遇到二分查找问题也就比较游刃有余了! LeetCode 刷题 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 分析题目:题目中提到中位数,可以考虑二分查找方法 还是以上面的数组为例,A数组为[1,2,4,9],B数组是[1,2,3,4,5,6,7,8] 具体分析:假设 B数组的3,也就是B[k/2-1] 比这k-2个元素都大。 当我们忽略掉 B数组中的元素后, k也要跟着减小,原来我们求第6小,现在就是求第3小。 整体求解过程,就是不断缩小数组的规模,同时把k也跟着缩小 经过这次比较后,A[k/2-1] < B[k/2-1],所以忽略掉A[0],然后将 k 变成2。 k此时等于2,k/2-1=>0 如果A[k/2-1] <= B[k/2-1],将A[0] - A[k/2-1]这些元素全部忽略掉 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。 给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。 分析题目:正常有序数组,查找对应的target值,只需要用二分查找方法进行查找元素。但是对于旋转排序而言,数组并不是一直有序的,只是局部有序 还有一种特殊的思路,对于旋转数组 nums = [4,5,6,7,0,1,2] 例如 target = 5, 目标值在左半段,因此在 [4, 5, 6, 7, inf, inf, inf] 这个有序数组里找就行了; 最终精髓:还是将「旋转数组中找目标值」 转化成了 「有序数组中找目标值」 给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。 如果数组中不存在目标值 target,返回 [-1, -1]。 题目分析: 根据升序数组来说,首先通过二分查找查找到第一个target值,然后再向右进行查找 具体思路: 代码实现:可以直接套用通用代码模板,查找一个数,然后加上一些判断条件即可。 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 解题思路:在排序数组中寻找是否存在一个目标值,可以直接用二分查找的方法 时间复杂度:O(logn),其中 n 为数组的长度。二分查找所需的时间复杂度为 O(logn)。 空间复杂度:O(1)。我们只需要常数空间存放若干变量。 【已知存在一个按非降序排列的整数数组 nums ,数组中的值不必互不相同】 题目分析:跟33题目类似,相当于升级版,主要区别是给点数组存在相同元素,还是采用二分查找的方法进行查询。 labuladong 的算法小抄和halfrost的LeetCode刷题手册,对我受益匪浅,现在推荐给大家,大家一起刷题,共勉!
可以看right 的值
【如果right = nums.length-1,那么while判断就是left<=right ,搜索空间[left , right]】
【如果right = nums.length,那么while判断就是left
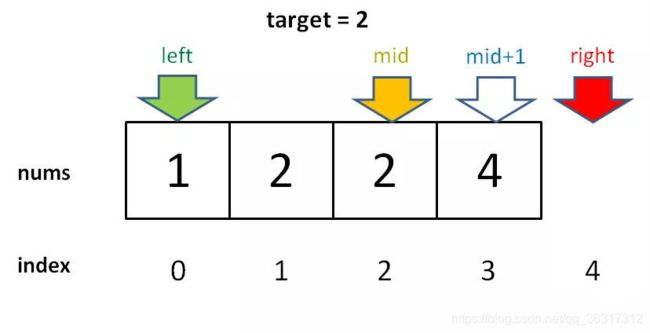
对于这个数组,算法会返回 1。这个 1 的含义可以这样解读:nums 中小于 2 的元素有 1 个。while (left < right) {
//...
}
// target 比所有数都大
if (left == nums.length) return -1;
// 类似之前算法的处理方式
return nums[left] == target ? left : -1;
if (nums[mid] == target)
right = mid;
int left_bound(int[] nums, int target) {
// 搜索区间为 [left, right]
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
// if else ...
}
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
所有元素都⼤时,会存在越界情况。if (left >= nums.length || nums[left] != target)
return -1;
return left;
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
// 搜索区间为 [left, right]
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
}
// 检查出界情况
if (left >= nums.length || nums[left] != target)
return -1;
return left;
}
寻找右侧边界的二分查找
int right_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = (left + right) / 2;
if (nums[mid] == target) {
left = mid + 1; // 注意
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1; // 注意
if (nums[mid] == target) {
left = mid + 1;
if (nums[mid] == target) {
left = mid + 1;
// 这样想: mid = left - 1
while (left < right) {
// ...
}
if (left == 0) return -1;
return nums[left-1] == target ? (left-1) : -1;
样这三个写法就完全统⼀了。int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 这⾥改成收缩左侧边界即可
left = mid + 1;
}
}
// 这⾥改为检查 right 越界的情况,⻅下图
if (right < 0 || nums[right] != target)
return -1;
return right;
}
总结
因此 初始化时 ,right = nums.length -1 >> 搜索空间[left , right] >> while(left <= right)
左右侧变化 left = mid +1 和 right = mid -1
当跳出循环的话,left = right +1 ,结束
因此 初始化时, right = nums.length >>搜索空间[left , right) >> while(left < right)
左右侧变化 left = mid +1 ,right= mid
当如果要跳出循环的话,需right = left
因为我们初始化 right = nums.length >>搜索空间是[left,right) >> while(leftint binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) { // 注意
int mid = (right + left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
// 搜索区间为 [left, right]
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
// 搜索区间变为 [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// 搜索区间变为 [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// 收缩右侧边界
right = mid - 1;
}
}
// 检查出界情况
if (left >= nums.length || nums[left] != target)
return -1;
return left;
}
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 这⾥改成收缩左侧边界即可
left = mid + 1;
}
}
// 这⾥改为检查 right 越界的情况,⻅下图
if (right < 0 || nums[right] != target)
return -1;
return right;
}
掌握了理论知识,下面就来进行实战,巩固所学习内容。4. 寻找两个正序数组的中位数
示例1
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例2
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
解决思路;
1、使用归并的方式,合并两个有序数组,得到一个大的有序数组。大的有序数组的中间位置的元素,即为中位数。
2、不用真正意义的合并,只需要找到中位数的位置即可
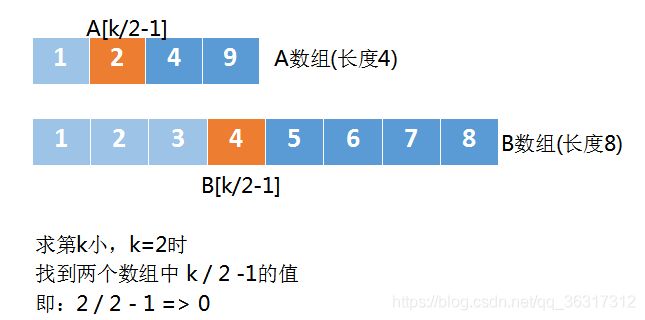
如图所示,假设有下面两个数组A 和 B,A数组的长度是4,B数组的长度是8, A+B总长度为12,是偶数,找到第6小和第7小的元素,相加/2即可

具体步骤:两个数组的中位数 >>转化为找到第k小的元素:
如果总长度N是偶数,则需要找到两个数组中第N / 2小的元素、第N / 2 + 1小的元素
如果总长度N是奇数,则需要找到两个数组中第N / 2 + 1小的元素
我们需要找第6、第7小的元素,假设我们先找第6小的元素,也就是k = 6。
我们首先比较 A数组中第3个元素,B数组中第3个元素,也就是A[k/2-1]和B[k/2-1]

由于A[k/2-1] > B[k/2-1],这时候我们就可以忽略掉一些元素了。
上图中 A数组中的4,它前面有2个元素,也就是k/2-1个元素,B数组的3,它前面也有2个元素,也就是k/2-1个元素,所以橙色的4和3前面一共有k-2个元素。
而 B[k/2-1] 是小于 A[k/2-1]的,那么B[k/2-1]相当于是第k-1小的,所以,第k小的元素肯定不是它。
这样的话,我们就可以排除一些元素了,刚才我们只是假设B[k/2-1] 比 A[k/2-1]前面的元素大,实际可能不是。
但有一点可以肯定,既然B[k/2-1]都不是第k小的元素,那么 B[k/2-1]前面的那些更不是了,于是我们将B[0]、B[1]、B[2]。。。B[k/2-1]这些元素全部忽略掉。

这次 k=3,k/2-1=>0
所以A[k/2-1]对应的就是A[0]
B[k/2-1]对应是B[3],因为我们之前忽略掉了 B数组中的前3个元素,所以B数组的第1个元素是从下标3开始的。 如下图:
于是A[k/2-1]对应的是A[1],因为刚才已经忽略掉A[0]了
B[k/2-1]对应的是B[3]
如下图:
当k==1时,返回A数组中第一个元素 和 B数组中第一个元素 的较小者。
此时A数组中的第1个元素是A[2],B数组中第1个元素是B[3],即求min(A[2],B[3])

还有一些特殊情况,A数组长度为2,B数组长度为10,求第6小时,A数组计算得到A[k/2-1]是A[2]越界了,对于这种情况,我们就拿 A数组中最后一个元素即可。

总结一下,对于求第k小的元素,其过程如下:
否则,将B[0] - B[k/2-1] 这些元素全部忽略掉
时间复杂度:O(log(m+n)),初始化长度为m+n,每次查询都会减半
空间复杂度:O(1)Python代码
class Solution(object):
def findMedianSortedArrays(self, nums1, nums2):
total = len(nums1) + len(nums2)
# 如果A数组长度+B数组长度total是奇数,则找total/2+1小的元素
# 即为中位数
if total % 2 == 1:
midIndex = total / 2 + 1
res = self.getKthElement(nums1, nums2, midIndex)
return float(res)
# 否则,找total/2,total/2+1这两个元素
else:
midIndex_1 = total / 2
midIndex_2 = total / 2 + 1
a = self.getKthElement(nums1, nums2, midIndex_1)
b = self.getKthElement(nums1, nums2, midIndex_2)
return (a + b) / 2.0
def getKthElement(self,nums1, nums2, k):
len1 = len(nums1)
len2 = len(nums2)
index1 = 0
index2 = 0
while True:
# 边界情况,当index1越界时,直接返回nums2的第k小元素
if index1 == len1:
return nums2[index2 + k -1]
# 边界情况,当index2越界时,直接返回nums1的第k小元素
if index2 == len2:
return nums1[index1 + k - 1]
# 边界情况,k等于1时,返回nums1第一个元素和nums2第一个元素较小者
if k == 1:
return min(nums1[index1], nums2[index2])
new_index1 = min(index1 + k / 2, len1) - 1
new_index2 = min(index2 + k / 2, len2) - 1
pivot1 = nums1[new_index1]
pivot2 = nums2[new_index2]
# 比较nums1[k/2-1]和nums2[k/2-1]
# 如果nums1的小,则忽略掉nums1[0] - nums1[k/2-1]这些元素
# 再更新 k,k 要减去忽略掉的那些元素,index1也要更新,待下轮使用
if pivot1 <= pivot2:
k -= (new_index1 - index1 + 1)
index1 = new_index1 + 1
# 如果nums2的小,则忽略掉nums2[0] - nums2[k/2-1]这些元素
# 再更新 k,k 要减去忽略掉的那些元素,index2也要更新,待下轮使用
else:
k -= (new_index2 - index2 + 1)
index2 = new_index2 + 1
java代码
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
int total = len1 + len2;
//如果A数组长度+B数组长度total是奇数,则找total/2+1小的元素即为中位数
if(total % 2 == 1) {
int midIndex = total / 2 + 1;
return getKthElement(nums1, nums2, midIndex);
}
//否则,找total/2,total/2+1这两个元素
else {
int midIndex_1 = total / 2;
int midIndex_2 = total / 2 + 1;
double a = getKthElement(nums1, nums2, midIndex_1);
double b = getKthElement(nums1, nums2, midIndex_2);
return (a + b) / 2.0D;
}
}
private int getKthElement(int[] nums1, int[] nums2, int k) {
int len1 = nums1.length;
int len2 = nums2.length;
int index1 = 0;
int index2 = 0;
while(true) {
//边界情况,当index1越界时,直接返回nums2的第k小元素
if(index1 == len1) {
return nums2[index2 + k - 1];
}
//边界情况,当index2越界时,直接返回nums1的第k小元素
if(index2 == len2) {
return nums1[index1 + k - 1];
}
//边界情况,k等于1时,返回nums1第一个元素和nums2第一个元素较小者
if(k == 1) {
return Math.min(nums1[index1], nums2[index2]);
}
int half = k / 2;
int newIndex1 = Math.min(index1 + half, len1) - 1;
int newIndex2 = Math.min(index2 + half, len2) - 1;
int pivot1 = nums1[newIndex1];
int pivot2 = nums2[newIndex2];
//比较nums1[k/2-1]和nums2[k/2-1]
//如果nums1的小,则忽略掉nums1[0] - nums1[k/2-1]这些元素
//再更新 k,k 要减去忽略掉的那些元素,index1也要更新,待下轮使用
if(pivot1 <= pivot2) {
k -= (newIndex1 - index1 + 1);
index1 = newIndex1 + 1;
}
//如果nums2的小,则忽略掉nums2[0] - nums2[k/2-1]这些元素
//再更新 k,k 要减去忽略掉的那些元素,index2也要更新,待下轮使用
else {
k -= (newIndex2 - index2 + 1);
index2 = newIndex2 + 1;
}
}
}
}
33. 搜索旋转排序数组
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
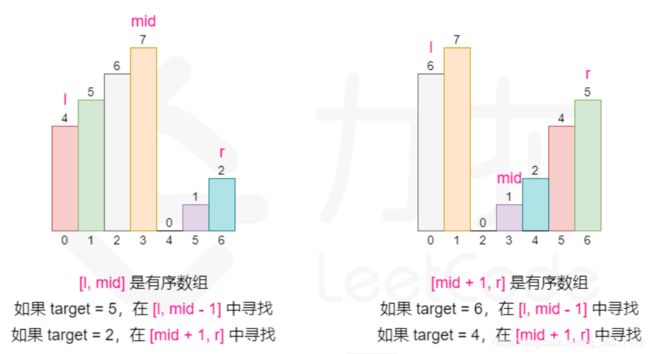
解题思路: 也可以进行二分查找方法进行查找,只是需要将数组分成左右两个部分,[4, 5, 6] 和 [7, 0, 1, 2] 两个部分,其中左边 [4, 5, 6] 这个部分的数组是有序的,根据有序的那个部分确定我们该如何改变二分查找的上下界,因为我们能够根据有序的那部分判断出 target 在不在这个部分:
class Solution:
def search(self, nums: List[int], target: int) -> int:
if not nums:
return -1
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
# 判断左数组是否为有序数组
if nums[0] <= nums[mid]:
if nums[0] <= target < nums[mid]:
right = mid - 1
else:
left = mid + 1
else:
if nums[mid] < target <= nums[len(nums) - 1]:
left = mid + 1
else:
right = mid - 1
return -1
首先根据 nums[0] 与 target 的关系判断 target 是在左段还是右段。
例如 target = 1, 目标值在右半段,因此在 [-inf, -inf, -inf, -inf, 0, 1, 2] 这个有序数组里找就行了。JAVA代码
class Solution {
public int search(int[] nums, int target) {
int low = 0 , height = nums.length - 1;
while(low <= height){
int mid = low +(height - low)/2;
if(nums[mid] == target){
return mid;
}
// 根据nums[0] 与target 的关系 判断目标值是在左半段还是右半段
if(target > nums[0]){
//目标值在左半段时,若 mid 在右半段,则将 mid 索引的值改成 inf
if(nums[mid] < nums[0]){
nums[mid] = Integer.MAX_VALUE;
}
} else {
//目标值在右半段时,若 mid 在左半段,则将 mid 索引的值改成 -inf
if(nums[mid] >= nums[0]){
nums[mid] = Integer.MIN_VALUE;
}
}
if(nums[mid] < target){
low = mid +1;
}else{
height = mid -1;
}
}
return -1;
}
}
34. 在排序数组中查找元素的第一个和最后一个位置
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
1、二分查找中,寻找leftIdx 即为在数组中寻找第一个大于等于target 的下标,寻找rightIdx 即为在数组中寻找第一个大于 target 的下标,然后将下标减一。
2、我们定义 binarySearch(nums, target, lower) 表示在nums 数组中二分查找 target 的位置,如果 lower 为true,则查找第一个大于等于 target 的下标,否则查找第一个大于target 的下标。
3、因为target 可能不存在数组中,因此我们需要重新校验我们得到的两个下标 leftIdx 和rightIdx,看是否符合条件,如果符合条件就返回 [leftIdx,rightIdx],不符合就返回 [-1,-1]python 代码
class Solution(object):
def searchRange(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
def binarySearch(nums, target):
left = 0
right = len(nums)-1
while left <= right :
mid = (left +right) // 2
if nums[mid]35. 搜索插入位置
你可以假设数组中无重复元素。示例 1:
输入: [1,3,5,6], 5
输出: 2
示例 2:
输入: [1,3,5,6], 2
输出: 1
class Solution {
public int searchInsert(int[] nums, int target) {
int left = 0;
int right = nums.length - 1; // 注意
while(left <= right) { // 注意
int mid = (right + left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
//如果没找到目标值,直接返回左侧索引即可
return left;
}
}
81. 搜索旋转排序数组 II
给你旋转后 的数组 nums 和一个整数 target ,请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false 。示例 1:
输入:nums = [2,5,6,0,0,1,2], target = 0
输出:true
示例 2:
输入:nums = [2,5,6,0,0,1,2], target = 3
输出:false
问题关键:无法根据元素的大小关系来划分数组。为什么不同的旋转点会导致「二段性丢失」:
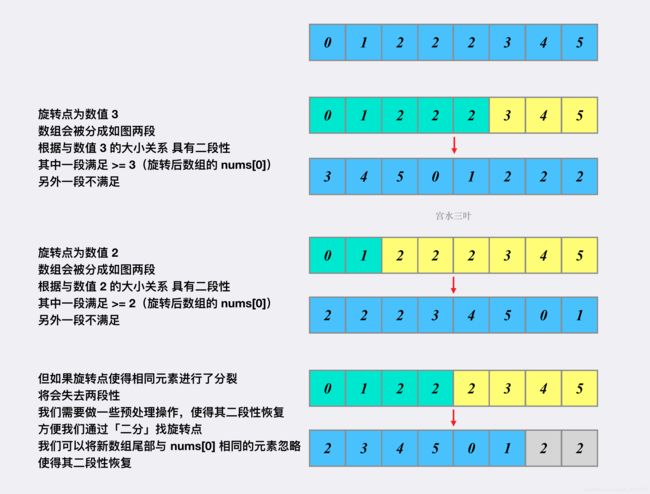
解题思路:
1、很多人觉得不必这么复杂,直接遍历一遍即可,这样说也没毛病。但是作为面试官的话,这种直接遍历的方案是次优的。
2、不妨考虑一下二分查找方法,具体思路:只有在nums[mid]严格大于或小于左边界时才能判断它左边或右边是升序的,这时可以再根据nums[mid], target与左右边界的大小关系排除掉一半的元素;当nums[mid]等于左边界时,无法判断是mid的左边还是右边是升序数组,而只能肯定左边界不等于target(因为nums[mid] != target),所以只能排除掉这一个元素,让左边界加一。直接遍历方法
class Solution {
public:
bool search(vector二分查找法
class Solution:
def search(self, nums: List[int], target: int) -> bool:
n = len(nums)
i, j = 0, n-1
while i <= j:
mid = i + (j - i) // 2
if nums[mid] == target:
return True
#左边有序
elif nums[mid] > nums[i]:
if nums[i] <= target < nums[mid]:
j = mid - 1
else:
i = mid + 1
#右边有序
elif nums[mid] < nums[i]:
if nums[mid] < target <= nums[j]:
i = mid + 1
else:
j = mid - 1
#当 nums[mid]等于左边界
elif nums[mid] == nums[i]:
i += 1
return False


同时需要这些资料的小伙伴们,可以关注一下“研行笔录”微信公众号,回复leetcode即可,还不快来领取leetcode刷题大礼包。
