机器学习——分类评价指标
本次介绍分类评价指标,使用二分类问题为例
这里我用一个小小的数据和逻辑模型来分析
我的需求是:利用已知的身高和体重去预测性别
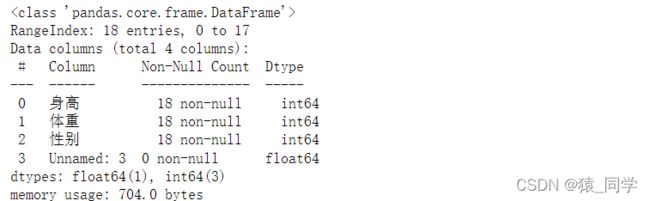
先导入数据并查看
import pandas as pd
data=pd.read_csv('sg.csv')
data.info()
进行数据预处理、删除无关特征、数据放缩
data.drop(['Unnamed: 3'],axis=1,inplace=True)
data['身高']=(data['身高']-data['身高'].min())/(data['身高'].max()-data['身高'].min())
data['体重']=(data['体重']-data['体重'].min())/(data['体重'].max()-data['体重'].min())
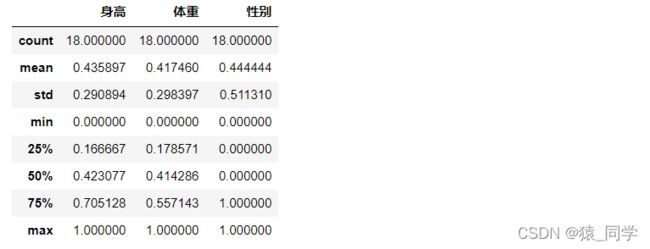
data.describe()再次查看数据,性别表示(0:男,1:女)
划分训练集和测试集
from sklearn.model_selection import train_test_split
X=data.drop('性别',axis=1)
y=data.性别
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.4)模型构建
from sklearn.linear_model import LogisticRegression
LR=LogisticRegression()
LR.fit(X_train,y_train)
print('训练集准确率:\n',LR.score(X_train,y_train))
print('测试集准确率:\n',LR.score(X_test,y_test))接下来就是来评价这模型的好坏了
预测测试集数据
混淆矩阵
根据学习器预测结果的对错,产生男女两类判断数据
例如垃圾邮件分类为例,TB和FB分别是重要文件和垃圾文件,TG和FG分别是垃圾文件和重要文件,可以看出,对角线TB和TG是预测出正确的选择,反对角线是预测错误的
二分类问题的混淆矩阵是一个2x2的情形分析表
| 真实情况 | 预测结果 | |
| 男 | 女 | |
| 男 | TB(真男) | FG(假女) |
| 女 | FB(假男) | TG(真女) |
从矩阵中得到得信息:
1、训练集的总数:TB+FB+TG+FG
2、训练集男数:TB+FG
3、训练集女数:FP+TN
4、分类错误的数:FB+FG
5、分类正确的数:TB+TG
当分类模型返回记录属于男性别的概率时,如果指定一个阈值,并将所有概率或评分在阈值以上的判断为男,可以得到一个混淆矩阵。通过连续改变阈值,可以得到多个不同的混淆矩阵。从而绘制出ROC曲线。
得到以上数据,我们就能得到这样四个指标
Precison(查准率):预测为男性的训练集中真正男性的比例
P = TB / (TB+FB)
Recall(召回率):真正为男性的训练集有多少被预测出来
R = TB / (TB+FG)
Accuracy(准确率):所有预测正确的结果占总观测值的比重
A=(TB+TG)/(TB+FB+FG+TG)
F1-score(F1分数):查准率与召回率的调和平均数
F1 = 2xRxP / (R+P)
其中F1-score的取值从0-1,1代表模型最好。0代表模型的输出结果最差
接下来我们用代码进行
y_pred=LR.predict(X_test)
from sklearn import metrics
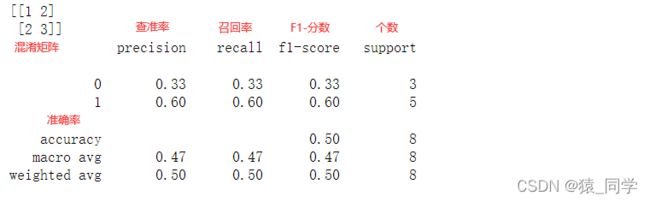
print(metrics.confusion_matrix(y_test,y_pred),)
print(metrics.classification_report(y_test,y_pred))print("查准率:",metrics.precision_score(y_test,y_pred))
print("召回率:",metrics.recall_score(y_test,y_pred))
print("F1分数:",metrics.f1_score(y_test,y_pred))
print("准确率:",metrics.accuracy_score(y_test,y_pred))
在大多数情况下类别的分类代价并不相等,即将样本分类为男性或女性的代价是不能相提并论的。
所有我们就可以把问题分成均衡分类问题和非均衡分类问题
接下来介绍非均衡分类问题
ROC曲线和AUC
ROC是一个用于度量分类中的非均衡性的工具,ROC曲线及AUC常被用来评价一个二值分类器的优劣。
为什么要使用ROC和AUC呢?
因为,在实际的数据集中经常会出现类别不平衡现象,即女性本比男性样本多很多(或者相反),而且测试数据中的男女样本的分布也可能随着时间而变化。而在这种情况下,ROC曲线能够保持不变。
ROC曲线可以用来比较不同分类器的相关性能。
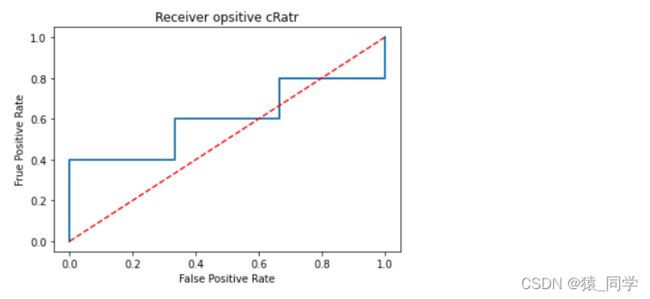
如图ROC曲线
横坐标为(假阳率)FPR:所有负例中有多少被预测为正例
![]()
纵坐标为(真阳率)TPR:有多少真正的正例被预测出来
![]()
特殊的几个点:
(0,0):FPR=TPR=0 ,即所有样本都被预测为女性样本;
(1,1):FPR=TPR=1,所有样本都被预测为男性样本;
(1,0):FPR=1,TPR=0,所有男性都被预测为女性,而所有男性都没被预测出来,它成功的避开了所有正确答案。
(0,1):FPR=0,TPR=1,这是一个完美的分类器,它将所有样本都正确分类。
所以经过上述分析,我们可以断言,ROC曲线越接近左上角,该分类器的性能越好,意味着分类器在假阳率很低的同时获得了很高的真阳率。
虚线y=x:这条对角线熵的点其实代表的是一个采用随机猜测策略的分类器的结果。
出现在右下角三角形中的任何分类器都比随机猜测更糟糕。
因此,在ROC图中,此三角形通常为空。
AUC的含义
AUC是一个概率值
作为评价ROC的指标,
为ROC的面积
取值在0.5~1之间
值越大分类器的效果越好
计算AUC的值代码实现:
#每个样例属于男性的概率值
y_pred_prob =LR.predict_proba(X_test)
#计算ROC曲线,既真阳率、假阳率等
fpr,tpr,thresholds = metrics.roc_curve(y_test,y_pred_prob[:,1])
#计算AUC值
auc1=metrics.auc(fpr,tpr)
print(auc1)
![]()
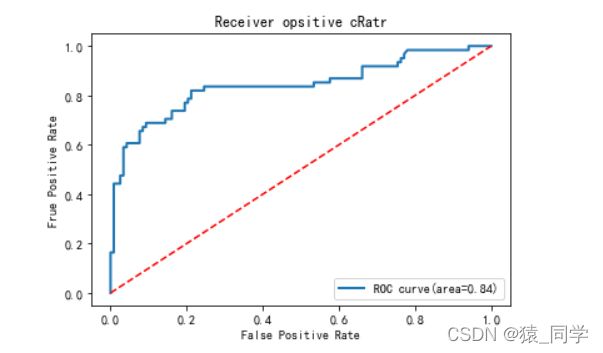
绘制ROC曲线
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(fpr,tpr,lw=2,label='ROC curve(area={:.2f})'.format(auc1))
plt.plot([0,1],[0,1],'r--')
plt.xlabel('False Positive Rate')
plt.ylabel('Frue Positive Rate')
plt.title('Receiver opsitive cRatr')