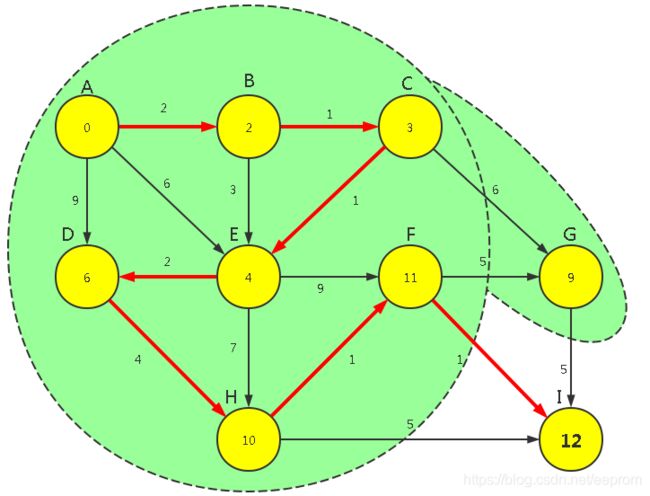
最短路dijkstra算法详解：dijkstra（图解）

最短路DijkStra’s Algorithm算法详解

dijkstra（图解）

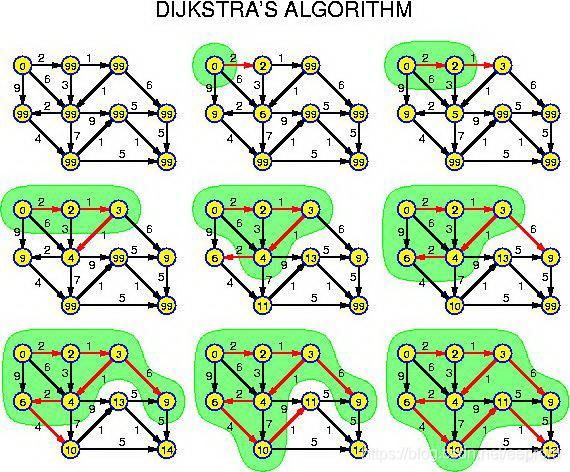
（额外说明一下:上面的图并非我原创,至少十几年前就已经存在了,哪位高人知道首次出现在哪里请告知我,我注明一下.）

概念：

源点:最开始的点,起点

终点:最后的点,目标到达的点

边权重Weight(m,n): 二维数组,代表连接顶点m到顶点n的边的权重值,即图上每条边的权重值.

顶点权重WeightMin(n): 一维数组,代表从起点到顶点n的所有通路上每条边权重之和的最小值.用来存放每一次计算的最小值.

FinalSet:已经确认的最终顶点的集合

图上数据说明: 顶点从左到右从上到下，坐标分别从0开始到8

Weight(m,n)的数据如下:

	n0	n1	n2	n3	n4	n5	n6	n7	n8
n0		2		9	6
n1			1
n2					4		6
n3								4
n4				2		9		7
n5							5		1
n6									5
n7						1			5
n8

算法基本原理

基础原理其实很朴素直白，就是从开始顶点（起点/源点）起，暴力穷举出能到达终止顶点（终点）的每一条通路并计算出距离。然后从所有的通路中找寻权重和最小的那一条通路。

不过这种朴素的找法有着明显缺点——随着顶点数增加，计算复杂度会上升得很快，(有多快?)粗略估算一下：

假设在有n个顶点的图内，用暴力方式穷举出从A点到B点之间所有可能的通路的总条数为$T_n$。当新增一个顶点进图后，顶点数从n个变为n+1个，A点到B点所有通路的总条数变为$T_{n+1}$。
如果我们找到了$T_{n+1}-T_n$是多少(或者知道这个值与n之间会有什么联系)，就可以大致知道这个增长率是多少了。

---

我们试想一下，新加入的这个顶点，它不可能是孤立存在的，它肯定会与原来(n顶点时)的图有连接的，并且连接的边数一定是大于等于2的。那么，现在我们再假设这新加进来的这个顶点与原图相连接的边的数量为m条，当我们要用暴力穷举法求解这n+1个顶点所有通路总条数时，可以在原来n个顶点的求解结果基础上，再从这m条新增的边里任意取2条边$C_m^2$，作为新顶点与原图连通时的入边与出边，从而形成一条新的通路。同时由于通路是具有方向性的，将同样的入边与出边对换一下则又是另一条通路，所以要乘以2，则n+1个顶点的总条数就应该是：
$$\begin{gathered} T_{n+1}=T_n+2\ast C_m^2=T_n+m\ast (m-1) \\ {T}_{n+1}-T_n=m^2-m \end{gathered}$$

---

也就是说，通路总数的单位增量（导数）是关于新增临接边数m的二次函数。如果新增的顶点能与原图大部分顶点都能连通，则m正比于n，那么使用暴力求解的总数$T_n$的表达式就应该约正比于顶点数n的三次方。但新增顶点一般并非都与原图的每个顶点都连通，它通常只连通它附近的那几个顶点，有时候（稀疏图时）m甚至可能退化为一个与顶点数无关的常数，所以暴力求解的计算复杂度与图内各顶点间连接的密集程度有关，用暴力求解计算复杂度的上限是关于顶点数n的三次方

所以需要在这个原理的基础上做优化，因为对于到达之前某个顶点的最短距离已经确定了之后，我们可以把该顶点的最短距离存起来，当计算它之后的顶点通路时，就直接拿出来用，而不需要再重头计算之前的那些顶点。（扩展阅读：这里用到的就是备忘录思想，将已经得到的最好结果存入备忘录，如果下次需要使用，则直接拿出来用，减少重复计算。详细请查阅动态规划里的备忘录）

优化后的算法就是不断重复以下2个步骤：

【P1】运行【广度优先算法】刷新附近顶点的顶点权重，优先找到最接近源点的所有可见点¹(↓脚注1:可见点解释↓)，计算这些可见点到源点的 距离长度² (↓脚注2:距离长度解释↓)，由于一个顶点可能会有多条通路通过，所以当再次计算该点到源点的另一条通路的距离长度时，要与之前已计算过的顶点权重WeightMin[n]取最小值,然后再更新该点的权重。

【P2】每当运行完单次【广度优先算法】后，使用【贪心算法】从所有已知路径中选择长度最短的那条路径，将其顶点归入最终顶点集合里FinalSet里

然后跳到该顶点运行【广度优先算法】，即再次进行【P1】，然后又进行【P2】，就这样一直重复(P1-P2-P1-P2-…)下去，直至最终图里所有点都进入FinalSet里为止。

脚注1:可见点
所谓可见点,是指能和已选顶点直接连通的点
不能和已选顶点直接连通的点都是不可见点

脚注2:距离长度
简单地讲,距离长度就是该点到源点的某条具体通路上所有边权重Weight(n,m)之和

---

距离长度等价于顶点权重,距离长度为了方便理解,顶点权重是为了方便存储距离长度.
(为什么要存储距离长度?)我们将某个点的距离长度保存下来,是为了当下次需要计算下一个顶点的距离长度时，不用将通路上所有边权重Weight(n,m)笨拙地全部求和一遍.而是直接使用保存下来的距离长度再加上新边的权重值Weight(n,m)就行了

【贪心算法】保证了进入FinalSet里的顶点距离一定是该点到源点所有可能路径中最短的，不可能有其他到达该点更短距离的路径(这个可以用反证法证明，假设存在另一条路径更短，可以推出矛盾的，我就不展开了)。

【广度优先算法】保证了在每次选择路径时，都不会漏掉任何一条可能的路径，并从这些可能的路径中找出最短的一条。

一般来说，【贪心算法】在很多时候并不都能找到全局最优解，只能得到局部最优解，我在文中虽然写的是“贪心算法”，但这只是为了帮助理解，实际上dijkstra运用的是【动态规划】的思想，结合【广度优先算法】从而保证了全局最优。

流程开始：

顶点对应关系:
node0: A
node1: B
node2: C
node3: D
node4: E
node5: F
node6: G
node7: H
node8: I

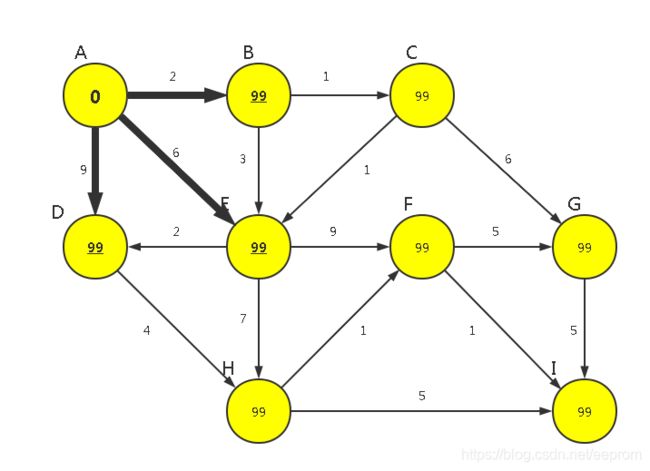
图1

将所有顶点权重WeightMin[]更新为无穷大,暂时以99代替（因为所有顶点权重和都没有比99更大的，可以用来代替无穷大）。

【P1】初始条件为无，可见点则只有起点自己，从自己到自己的权重为0，WeightMin[0]=0，其余都是不可见点，都设置为99。

【P2】将顶点0（A点）归入最终顶点集合里FinalSet里，FinalSet[]={0}，此时FinalSet未包含全部顶点，所以即将对顶点0（A点）运行【广度优先算法】

---

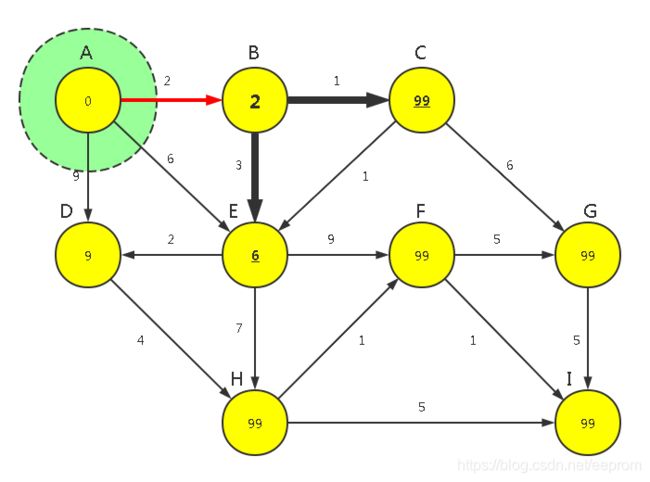
图2

【P1】对顶点0（A点）运行【广度优先算法】，确认可见点为n1,n3,n4（BDE点）这3点，计算其所有可见点到源点n0通路的距离长度（使用已知的WeightMin[0]加上其直接连接的各边的权重Weight[0,(n1,n3,n4)]），分别是[0+2,0+9,0+6]。然后与之前这3个点的顶点权重WeightMin[[1,3,4]]:[99,99,99]进行比较，取最小值(2<99,9<99,6<99)然后再更新，所以最后刷新这3点的顶点权重WeightMin[[1,3,4]]=[2,9,6]。

【P2】从所有已知路径顶点n1(2),n3(9),n4(6)中找长度最短的那条，顶点n1（即B点），将其纳入最终顶点集合FinalSet={0,1}，此时FinalSet未包含全部顶点，所以即将对顶点1（B点）运行【广度优先算法】

---

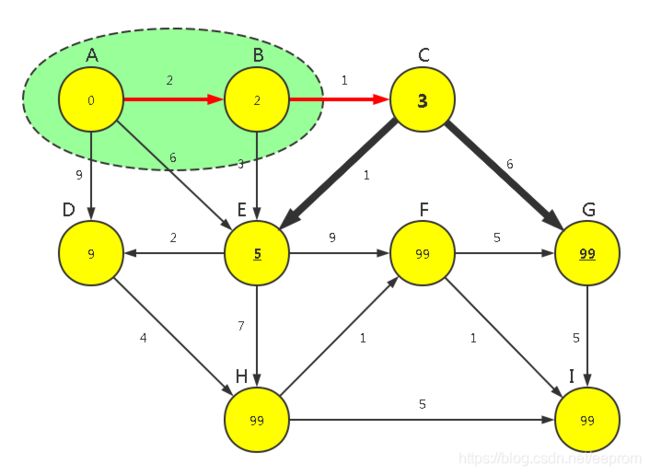
图3

【P1】对顶点1（B点）运行【广度优先算法】，确认可见点为n2,n4（CE点）这2点，计算所有可见点到源点通路的距离长度WeightMin[1]+Weight[1,(n2,n4)]=[2+1,2+3]。然后与之前的顶点权重WeightMin[[2,4]:[99,6]进行比较更新，WeightMin[[2,4]]=[3,5]。

【P2】从所有已知路径顶点n2(3),n3(9),n4(5)中找长度最短的那条，是顶点n2（C点），将其纳入最终顶点集合FinalSet={0,1,2}，此时FinalSet未包含全部顶点，所以即将对进来的顶点2（C点）运行【广度优先算法】

---

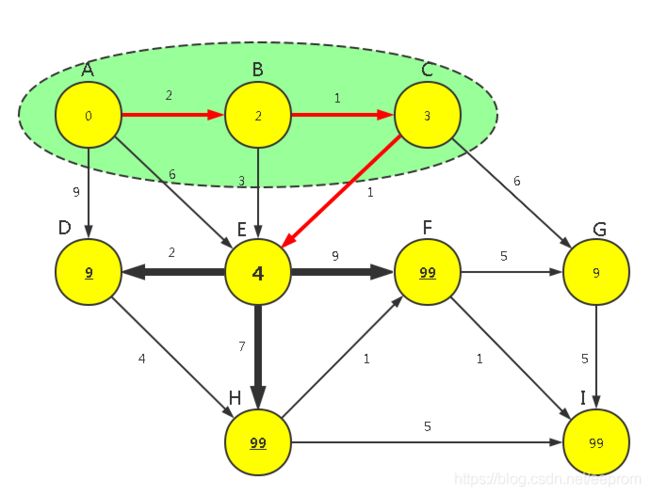
图4

【P1】对顶点2（C点）运行【广度优先算法】，确认可见点为n4,n6（EG点）这2点，计算所有可见点到源点的通路的距离长度WeightMin[2]+Weight[1,(n4,n6)]=[3+1,3+6]。然后与之前的WeightMin[[4,6]:[5,99]进行比较更新，WeightMin[[4,6]=[4,9]。

【P2】从所有已知路径顶点n3(9),n4(4),n6(9)中找长度最短的那条，是顶点n4（E点），将其纳入最终顶点集合FinalSet={0,1,2,4}，此时FinalSet未包含全部顶点，所以即将对进来的顶点4（E点）运行【广度优先算法】

---

图5

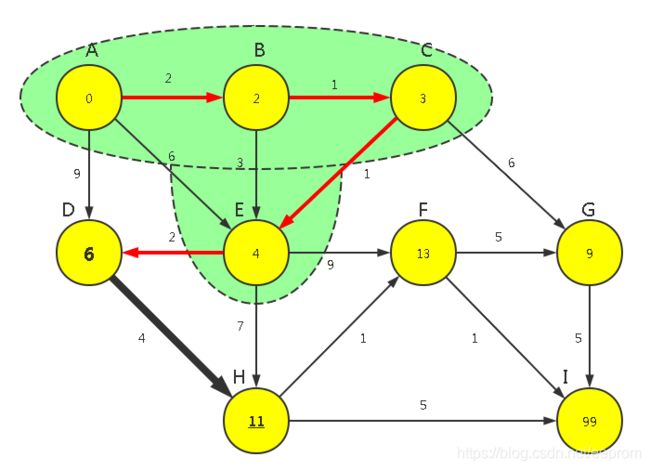
【P1】对上次归入FinalSet的顶点运行【广度优先算法】求所有可见点的距离长度

g(n4) => (n3,n5,n7)

w(n3,n5,n7)=WeightMin[4]+Weight[4,(n3,n5,n7)]=[4+2,4+9,4+7]=[6,13,11]

WeightMin[[3,5,7]] = min([6,13,11] ,WeightMin[[3,5,7]]) = min([6,13,11] ,[9,99,99])=[6,13,11]

【P2】从所有已知路径顶点(=上一次全部顶点 - 上一次选中顶点 + 本次可见点)中选出长度最短的那条的顶点，归入FinalSet

min{n3,n5,n6,n7} = min{WeightMin[[3,5,6,7]]}=min([6,13,9,11])=6

n3

FinalSet={0,1,2,3,4}

---

图6

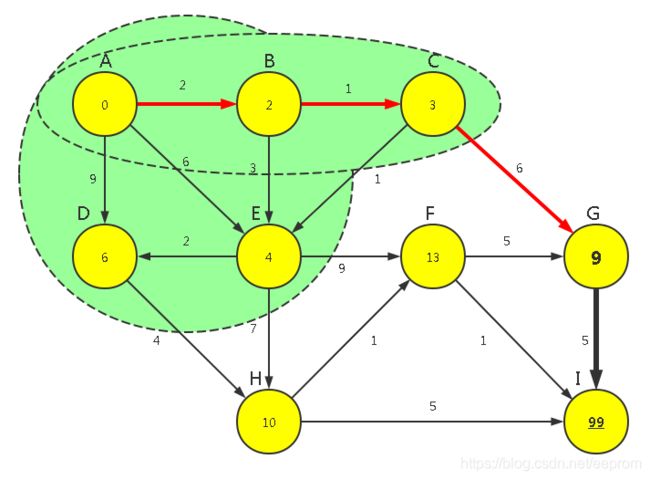
【P1】对上次归入FinalSet的顶点运行【广度优先算法】求所有可见点的距离长度

g(n3) => (n7)

w(n7) = WeightMin[3]+Weight[3,(n7)] = [6+4] = [10]

WeightMin[7] = min([10] ,WeightMin[7]) = min([10] ,[11]) = [10]

【P2】在所有已知路径中选出最短路径对应的顶点，归入FinalSet

min{n5,n6,n7} = min{WeightMin[[5,6,7]]} = min([13,9,10]) = 9

n6

FinalSet={0,1,2,3,4,6}

---

图7

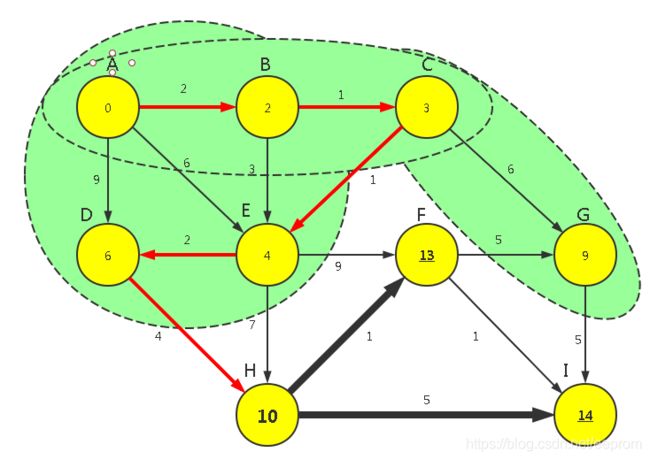
【P1】对上次归入FinalSet的顶点运行【广度优先算法】求所有可见点的距离长度

g(n6) => (n8)

w(n8) = WeightMin[6]+Weight[6,(n8)] = [9+5] = [14]

WeightMin[8] = min([14] ,WeightMin[8]) = min([14] ,[99]) = [14]

【P2】在所有已知路径中选出最短路径对应的顶点，归入FinalSet

min{n5,n7,n8} = min{WeightMin[[5,7,8]]} = min([13,10,14]) = 10

n7

FinalSet={0,1,2,3,4,6,7}

---

图8

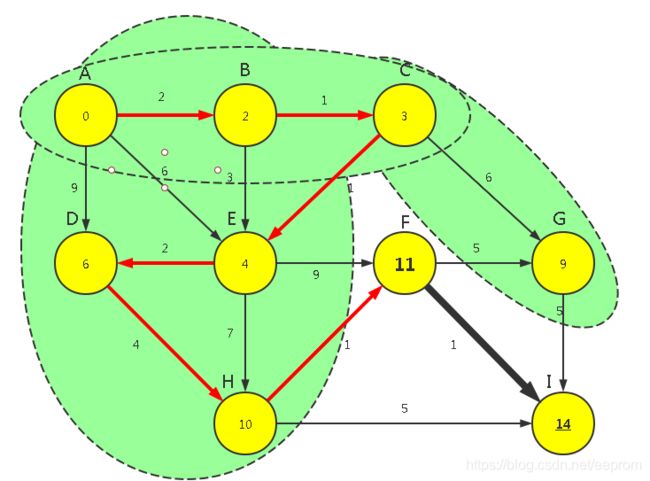
【P1】对上次归入FinalSet的顶点运行【广度优先算法】求所有可见点的距离长度

g(n7) => (n5,n8)

w(n5,n8) = WeightMin[7]+Weight[7,(n5,n8)] = [10+1,10+5] = [11,15]

WeightMin[[5,8]] = min([11,15] ,WeightMin[[5,8]]) = min([11,15] ,[13,14]) = [11,14]

【P2】在所有已知路径中选出最短路径对应的顶点，归入FinalSet

min{n5,n8} = min{WeightMin[[5,8]]} = min([11,14]) = 11

n5

FinalSet={0,1,2,3,4,6,7,5}

---

图9

【P1】对上次归入FinalSet的顶点运行【广度优先算法】求所有可见点的距离长度

g(n5) => (n8)

w(n8) = WeightMin[5]+Weight[5,(n8)] = [11+1] = [12]

WeightMin[8] = min([12] ,WeightMin[8]) = min([12] ,[14]) = [12]

【P2】在所有已知路径中选出最短路径对应的顶点，归入FinalSet

min{n8} = min{WeightMin[8]} = min([12]) = 12

n8

FinalSet={0,1,2,3,4,6,7,5,8}

至此，所有顶点都进入FinalSet里

算法终止

---

1. 脚注1: 所谓可见点,是指能和已知顶点直接连通的点 ↩︎

2. 脚注2: 将某条通路上所有顶点Weight(n,m)求和并保存到WeightMin(n)中，当下次计算下一个顶点的时候，就可以直接使用这次的WeightMin(n)再加上边的权重值Weight(n,m)了 ↩︎