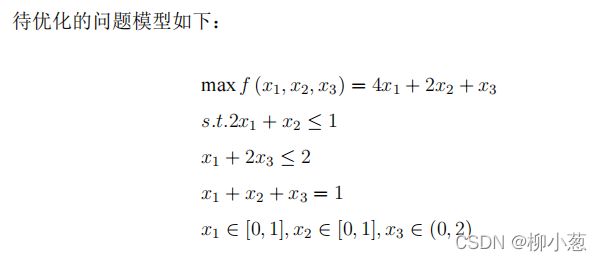python遗传算法之单/多目标规划问题
在上一篇博客中,我们学习了python遗传算法包geatpy。并用它展示了一个不带约束的单目标规划问题,对往期内容感兴趣的同学可以参考:
- 链接: python遗传算法之geatpy学习.
在上一期的介绍中,我们用遗传算法求解时,采用的是类似matlab式的非面向对象编程,导致每一步写的都很繁琐,今天我们采用面向对象编程的方式来简化求解过程。
目录
- 1. 运行环境
- 2. 面向对象的原理
- 3. 带约束的单目标优化问题
-
- 3.1 继承 Problem 问题类完成对问题模型的描述
- 3.2 调用算法模板进行求解
- 3.3 结果
- 4. 带约束的多目标优化问题
-
- 4.1 继承 Problem 问题类完成对问题模型的描述
- 4.2 调用算法模板进行求解
- 4.3 结果
- 5. 参考资料
1. 运行环境
这里先介绍一下运行环境
- 系统:Windows10
- 配置:i7-6700 16G
- python版本:3.10
- geatpy版本:2.7.0
2. 面向对象的原理
前面的章节中,我们介绍了遗传算法主要分为算法模板类 (Algorithm)、种群类 (Population)、多染色体混合编码种群类 (PsyPopulation) 以及问题类 (Problem)。其中 Population 类和 PsyPopulation 类是可以直接被实例化成对象去来使用的类;Algorithm 类和 Problem 类是父类,需要实例化其子类来使用。下面我们通过案例来演示一下用法。
3. 带约束的单目标优化问题
3.1 继承 Problem 问题类完成对问题模型的描述
在这一步中,主要是将我们的问题按照模板描述清楚,包括目标函数和约束条件。
import numpy as np
import geatpy as ea
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self):
name = 'MyProblem' # 初始化name(函数名称,可以随意设置)
M = 1 # 初始化M(目标维数)
maxormins = [-1] # 初始化目标最小最大化标记列表,1:min;-1:max
Dim = 3 # 初始化Dim(决策变量维数)
varTypes = [0] * Dim # 初始化决策变量类型,0:连续;1:离散
lb = [0, 0, 0] # 决策变量下界
ub = [1, 1, 2] # 决策变量上界
lbin = [1, 1, 0] # 决策变量下边界
ubin = [1, 1, 0] # 决策变量上边界
# 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb,
ub, lbin, ubin)
def aimFunc(self, pop): # 目标函数,pop为传入的种群对象
Vars = pop.Phen # 得到决策变量矩阵
x1 = Vars[:, [0]] # 取出第一列得到所有个体的x1组成的列向量
x2 = Vars[:, [1]] # 取出第二列得到所有个体的x2组成的列向量
x3 = Vars[:, [2]] # 取出第三列得到所有个体的x3组成的列向量 # 计算目标函数值,赋值给pop种群对象的ObjV属性
pop.ObjV = 4 * x1 + 2 * x2 + x3
# 采用可行性法则处理约束,生成种群个体违反约束程度矩阵
pop.CV = np.hstack([2 * x1 + x2 - 1, # 第一个约束
x1 + 2 * x3 - 2, # 第二个约束
np.abs(x1 + x2 + x3 - 1)]) # 第三个约束
3.2 调用算法模板进行求解
在第二步中,我们主要编写的是算法模板对第一步中问题的定义进行求解,这里需要依次设置种群、算法参数、种群进化、结果的输出。
"""main_solve.py"""
import geatpy as ea # import geatpy
from myaim import MyProblem # 导入自定义问题接口
"""============================实例化问题对象========================"""
problem = MyProblem() # 实例化问题对象
"""==============================种群设置==========================="""
Encoding = 'RI' # 编码方式
NIND = 50 # 种群规模
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges,problem.borders) # 创建区域描述器
population = ea.Population(Encoding, Field, NIND) # 实例化种群对象(此时种群还没被真正初始化,仅仅是生成一个种群对象)
"""===========================算法参数设置=========================="""
myAlgorithm = ea.soea_DE_best_1_L_templet(problem, population) # 实例化一个算法模板对象
myAlgorithm.MAXGEN = 1000 # 最大进化代数
myAlgorithm.mutOper.F = 0.5 # 差分进化中的参数F
myAlgorithm.recOper.XOVR = 0.7 # 设置交叉概率
myAlgorithm.logTras = 1 # 设置每隔多少代记录日志,若设置成0则表示不记录日志
myAlgorithm.verbose = True # 设置是否打印输出日志信息
myAlgorithm.drawing = 1 # 设置绘图方式(0:不绘图;1:绘制结果图;2:绘制目标空间过程动画;3:绘制决策空间过程动画)
"""==========================调用算法模板进行种群进化==============="""
[BestIndi, population] = myAlgorithm.run() # 执行算法模板,得到最优个体以及最后一代种群
BestIndi.save() # 把最优个体的信息保存到文件中
"""=================================输出结果======================="""
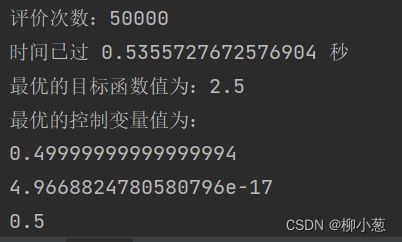
print('评价次数:%s' % myAlgorithm.evalsNum)
print('时间花费 %s 秒' % myAlgorithm.passTime)
if BestIndi.sizes != 0:
print('最优的目标函数值为:%s' % BestIndi.ObjV[0][0])
print('最优的控制变量值为:')
for i in range(BestIndi.Phen.shape[1]):
print(BestIndi.Phen[0, i])
else:
print('此次未找到可行解。')
3.3 结果
4. 带约束的多目标优化问题
4.1 继承 Problem 问题类完成对问题模型的描述
对于多目标的问题,依旧是先编写目标规划问题。
import numpy as np
import geatpy as ea
class MyProblem(ea.Problem): # 继承Problem父类
def __init__(self):
name = 'BNH' # 初始化name(函数名称,可以随意设置)
M = 2 # 初始化M(目标维数)
maxormins = [1] * M # 初始化maxormins
Dim = 2 # 初始化Dim(决策变量维数)
varTypes = [0] * Dim # 初始化varTypes(决策变量的类型,0:实数;1:整数)
lb = [0] * Dim # 决策变量下界
ub = [5, 3] # 决策变量上界
lbin = [1] * Dim # 决策变量下边界
ubin = [1] * Dim # 决策变量上边界 # 调用父类构造方法完成实例化
ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb,ub, lbin, ubin)
def aimFunc(self, pop): # 目标函数
Vars = pop.Phen # 得到决策变量矩阵
x1 = Vars[:, [0]] # 注意这样得到的x1是一个列向量,表示所有个体的x1
x2 = Vars[:, [1]]
f1 = 4*x1**2 + 4*x2**2
f2 = (x1 - 5)**2 + (x2 - 5)**2
# 采用可行性法则处理约束
pop.CV = np.hstack([(x1 - 5)**2 + x2**2 - 25,-(x1 - 8)**2 - (x2 - 3)**2 + 7.7])
# 把求得的目标函数值赋值给种群pop的ObjV
pop.ObjV = np.hstack([f1, f2])
## 目标函数主要需要计算出CV和ObjV
4.2 调用算法模板进行求解
模板求解,和单目标规划类似。
import geatpy as ea # import geatpy
from ga_more_aim import MyProblem # 导入自定义问题接口
import numpy as np
"""=======================实例化问题对象==========================="""
problem = MyProblem() # 实例化问题对象
"""=========================种群设置=============================="""
Encoding = 'RI' # 编码方式
NIND = 100 # 种群规模
Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges,problem.borders) # 创建区域描述器
population = ea.Population(Encoding, Field, NIND) # 实例化种群对象(此时种群还没被真正初始化,仅仅是生成一个种群对象)
"""=========================算法参数设置============================"""
myAlgorithm = ea.moea_NSGA2_templet(problem, population) # 实例化一个算法模板对象
myAlgorithm.mutOper.Pm = 0.2 # 修改变异算子的变异概率
myAlgorithm.recOper.XOVR = 0.9 # 修改交叉算子的交叉概率
myAlgorithm.MAXGEN = 200 # 最大进化代数
myAlgorithm.logTras = 1 # 设置每多少代记录日志,若设置成0则表示不记录日志
myAlgorithm.verbose = False # 设置是否打印输出日志信息
myAlgorithm.drawing = 1 # 设置绘图方式(0:不绘图;1:绘制结果图;2:绘制目标空间过程动画;3:绘制决策空间过程动画)
"""==========================调用算法模板进行种群进化==============
调用run执行算法模板,得到帕累托最优解集NDSet以及最后一代种群。
NDSet是一个种群类Population的对象。
NDSet.ObjV为最优解个体的目标函数值;NDSet.Phen为对应的决策变量值。
详见Population.py中关于种群类的定义。
"""
[NDSet, population] = myAlgorithm.run() # 执行算法模板,得到非支配种群以及最后一代种群
NDSet.save() # 把非支配种群的信息保存到文件中
"""===========================输出结果========================"""
print('用时:%s 秒' % myAlgorithm.passTime)
print('非支配个体数:%d 个' % NDSet.sizes) if NDSet.sizes != 0 else print('没有找到可行解!')
if myAlgorithm.log is not None and NDSet.sizes != 0:
print('GD', myAlgorithm.log['gd'][-1])
print('IGD', myAlgorithm.log['igd'][-1])
print('HV', myAlgorithm.log['hv'][-1])
print('Spacing', myAlgorithm.log['spacing'][-1])
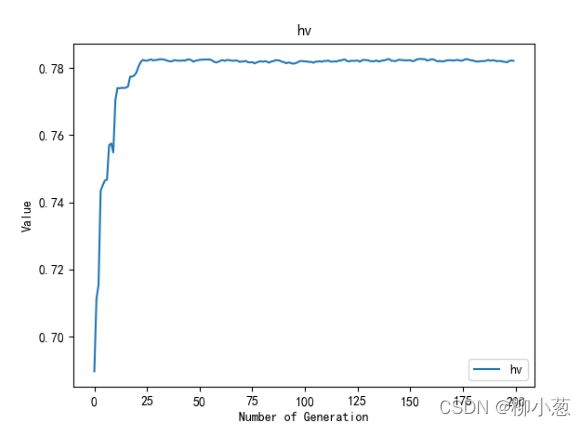
"""======================进化过程指标追踪分析=================="""
metricName = [['igd'], ['hv']]
Metrics = np.array([myAlgorithm.log[metricName[i][0]] for i in range(len(metricName))]).T
# 绘制指标追踪分析图
ea.trcplot(Metrics, labels=metricName, titles=metricName)
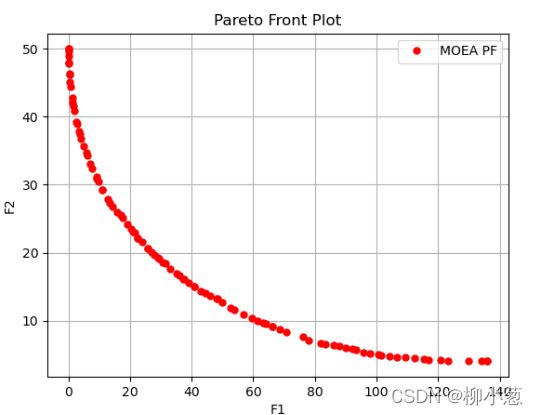
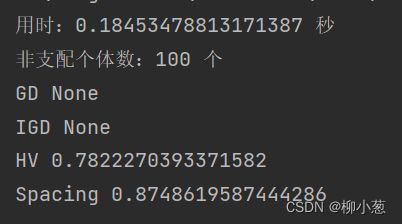
4.3 结果
很多初学者可能不太清楚评价多目标规划的一些指标GD、IGD、HV等,这里给大家参考: 多目标进化算法的性能评价指标总结.
5. 参考资料
- geatpy官网教程: https://geatpy.com.
- 多目标规划评价指标: 多目标进化算法的性能评价指标总结.