python遗传算法解简单整数规划与原理探究
文章目录
- 一、算例与代码
-
- 1.1 问题与思路
- 1.2 代码
- 二、实现细节
-
- 2.1 什么是种群
- 2.2 编码与解码
- 2.3 如何处理约束
- 2.4 如何从较好解获得新的解
- 三、反思:真的是采样逼近吗 / 消融实验
-
- 3.1 最优解和较好解的关系 / 遗传算法为什么可行
- 3.2 为什么交叉能得到更优解
- 3.3 为什么交叉具有附近采样的特点
- 3.4 消融实验:你真的需要编码、变异与交叉吗
-
- 3.4.1 二进制编码
- 3.4.2 变异
- 3.4.3 交叉
- 3.4.4 那么,还需要编码、交叉、变异吗
最近写交通运输经济学作业,遇到一个求解最小飞机运输成本的整数规划问题,就尝试着实现了一个简单的遗传算法进行求解,效果还行,故记录下来。同时也记录一下实现遗传算法的一些细节,以及实现过程中的一些想法。这里的遗传算法代码可以简单迁移到类似的整数规划任务上。
在开始阅读之前,可以先看看这篇文章:
袋鼠蹦跳:https://www.jianshu.com/p/ae5157c26af9
一、算例与代码
1.1 问题与思路
简化后的问题如下:
从机场A到机场B有两种飞机可用于航班飞行:一种是20座的小飞机,每排班一架所需的成本是4万美元;另一种是150座的大飞机,每排班一架所需的成本是15万美元。
求解:若某天有 N N N个乘客(在本题中大约几千个)需要从机场A去机场B,应排班多少架大飞机,多少架小飞机,使得在满足所有乘客出行需求的前提下,总的运输成本最小?
思路1:
这是一个简单的整数规划问题,其求解目标与约束条件如下:
M i n c o s t = 4 x + 15 y s . t . 20 x + 150 y ≥ N x , y ≥ 0 ; x , y ∈ Z Min \ cost=4x+15y \\ s.t. \ 20x+150y \geq N \\ x,y \geq 0;x,y \in \mathbb{Z} Min cost=4x+15ys.t. 20x+150y≥Nx,y≥0;x,y∈Z
其中 x x x是所需小飞机数量, y y y是所需大飞机数量,求解即可得到x、y。求解方法有分支界定、割平面等方法,也可以用python的cvxpy库、matlab等方式求解。
思路2:
但是实际上,在解这个问题时,没有人会去写上述的整数规划表达式,再解这个式子。
比较自然的想法是:既然大飞机的性价比较高,那么可以先尽量排满大飞机,直到剩下的一部分乘客不足以坐满一架大飞机。对于剩下的乘客,再尝试一下用多架小飞机,与用一架大飞机全部装载的成本,选择成本较低的方案即可。
从感觉上来说,我们通过分析和经验,能够大概猜到最优解在哪个范围(飞机数量不能太少否则载不完乘客,优先使用大飞机),然后我们在这个范围中多调整几次(试一下最后用一架大飞机还是多架小飞机装载),就可以找到最优解了。
思路3:
回想一下思路2中“自然的想法”,我的具体的思考过程是这样的:
- 我拿到这个问题的时候,自然的去想象一些不同的情况,在脑中模拟了一下不同乘客数、不同飞机数量、不同飞机类型下的具体情境,就能够发现一些规律:飞机越多,能装载的乘客数越多,越能轻松的载完所有乘客;但是飞机不能太多,否则会多出无意义的成本;尽量让所有飞机满载可以降低成本;在搭载同样数量乘客且满载时,大飞机成本更低
- 总结出了一些规律,我对最优解的范围已经有了一定的感觉:首先最优解时大部分的飞机都应该处在满载状态,并且能够装完所有乘客;最优解情况下若能满载,一定会优先使用大飞机载客。所以先把乘客尽量用大飞机装满
- 如果最后一架大飞机载不满,这时可能用多架小飞机省钱,也可能用一架大飞机省钱
- 最后确定最优解,只需要把这两种情况算一算,比较一下就行了。思路2中自然的想法随即产生
总结一下,“自然的想法”来源于这样一个过程:尝试–>总结现象,发现规律–>通过规律缩小最优解范围–>没法在缩小最优解范围–>把范围内的解都尝试一遍,找到最优解。
把范围内的解都尝试一遍,就是在范围内不断采样,不断计算,类似于通过排除法缩小最优解范围,直到找到最优解。
找规律的尝试,最后试解,都可以形容为一个随机采样的过程。不断用找到的规律缩小最优解范围,最后采样试解缩小最优解范围,则可以形容为一个调整逼近的过程。
这时候,我产生了一个大胆的想法:在思路2中调整逼近最优解,用了两个策略——找规律与随机采样,而找规律本身也依赖于随机采样。那么我们能不能仅通过随机采样,不总结规律,直接进行调整逼近呢?
这就是遗传算法的整体思路:在解空间中随机采样很多个解–>挑出一些较好的解–>在较好的解附近采样,得到很多新解–>重复进行上述第二、第三步,直到新解收敛到最优解。
其他博客的对应表达为:初始化种群–>评估个体适应度与自然选择–>交叉与变异–>演化迭代
比起其他博客从进化的过程阐述,我更倾向于把遗传算法描述成一种采样逼近的求解策略。采样就是初始化种群、交叉与变异。逼近就是自然选择,而交叉本身也暗含逼近。
这套求解策略十分巧妙,具体的原理将会在第三部分简要分析。先上代码、实现细节、一些处理策略。
1.2 代码
下面是整数规划的遗传算法代码实现,有一些实现细节与其他博客不同,不过解决这个简单整数规划的效果还是不错的。当问题复杂后可能要增加初始化种群的规模与迭代次数,或者更改自然选择策略。
首先调库:
import numpy as np
import random
import matplotlib.pyplot as plt
遗传算法代码(一行流版):输入乘客数,输出最优方案与对应运输成本
def get_plan_based_on_GA(cks):
zq=np.random.randint(0,2,(1000,10+7)) #初始化种群,编码encoder:17位二进制数字,小飞机10位大飞机7位,即乘客上限20480+19200人
decoder=lambda x:np.sum(np.power(2,np.arange(x.shape[-1]-1,-1,-1))*x, axis=1).reshape((-1,1)) #二进制转十进制
singlepoint_crossover=lambda x,po=random.randint(0,zq.shape[1]-3):np.hstack((x[0][:po],x[1][po:po+3],x[0][po+3:])) #单点交叉,输入[[编码1],[编码2]]
costlist=[]
for _ in range(10):
plan=np.hstack((decoder(zq[:,0:10]),decoder(zq[:,10:17]))) #将二进制编码解码为方案
kill=np.dot(plan,np.array([[20],[150]])) < cks #选出承载力小于乘客人数的方案
zq=np.delete(zq, np.where(kill), axis=0) #清理种群,清除所有不满足载客量要求的个体
plan=np.delete(plan, np.where(kill), axis=0) #清理种群,清除所有不满足载客量要求的个体
cost=np.dot(plan,np.array([[4],[15]])) #运输成本
select=np.max(cost)/cost #选择概率,成本越小,select概率越大
deleteindex=np.argsort(select.reshape(-1))[:int(select.shape[0]*0.7)] #贪心选择,对选择概率排序然后删除后0.7,保留前0.3
zq=np.delete(zq, deleteindex, axis=0) #进行选择,得到选择后的新种群
jc=np.array([singlepoint_crossover(zq[np.random.randint(0,zq.shape[0],(2))]).tolist() for o in range(700)]) #得到交叉的子群
by=np.abs(jc-(np.random.random(jc.shape)>0.95)) #变异,有0.05概率把对应位置值换一下
zq=np.vstack((zq,by)) #将父代与子代拼起来,得到新种群
costlist.append(np.min(cost)) #记录最小开销
plt.plot(range(len(costlist)),costlist)
return plan[np.argmin(cost)], np.min(cost)
print(get_plan_based_on_GA(5644))
代码的实现尽量利用numpy并行处理避免循环,为了整体思路清楚尽量用一行代码实现一个功能。代码的实现细节会和遗传算法的具体实现一起在下文说明。
二、实现细节
这个部分按照代码的逻辑顺序介绍了实现细节,并穿插了一些个人对于遗传算法的理解。
一些名词的对应关系:
种群 = = =一堆个体(这里是1000个)的集合 = = =一堆解的集合 = = =一个1000×17的0-1二维张量
个体 = = =染色体=一个解 = = =一个排班方案 = = =一个17维0-1向量
父代 = = =自然选择后的种群 = = =原一堆解中的较优可行解 = = =父代个体个数×17维的0-1二维张量
子代 = = =父代交叉变异后得到的新子群 = = =一堆新解 = = =子代个体个数×17维的0-1二维张量
2.1 什么是种群
种群其实就是一堆解,初始化种群其实就是在解空间中随机采样一堆解。代码实现非常简单,就是生成一个1000×17的随机0-1矩阵,相当于随机采样了1000个解,生成了1000个个体。
zq=np.random.randint(0,2,(1000,10+7)) #初始化种群
但是根据原始的问题,我们要求的目标只有两个:小飞机数量x和大飞机数量y。也就是说,解应该是一个二维非负整数向量 ( x , y ) (x,\ y) (x, y),为什么这里的解变成了一个17维0-1向量?这就涉及到编码与解码。
2.2 编码与解码
编码实际上就是建立一个一一对应的映射规则,把原来的解空间映射到高维的解空间,因此可以认为每个个体就是一个解。在这里用的是二进制编码。二进制编码有一些优秀的性质,方便进行遗传算法的变异、交叉,在后文会进行分析。
这里的编码规则是:将小飞机数量 x x x用10位二进制(换成10进制最大是1024)表示,大飞机数量 y y y用7位二进制(换成十进制最大是128)表示,然后将这两个二进制数拼成一个17维0-1向量。
这样小飞机最多可以安排1024架,最多搭载20480人;大飞机最多可安排128架,最多搭载19200人。由于求解的乘客数大概是几千人,这样编码为乘客数留出了很多冗余,能够保证解空间覆盖最优解。
解码就是简单的将二进制数转化为十进制即可,具体的二进制、十进制转化的操作可以看这里:https://zhuanlan.zhihu.com/p/75291280
如下图所示,某一个体解码出来的排班计划是:小飞机207架,大飞机38架。
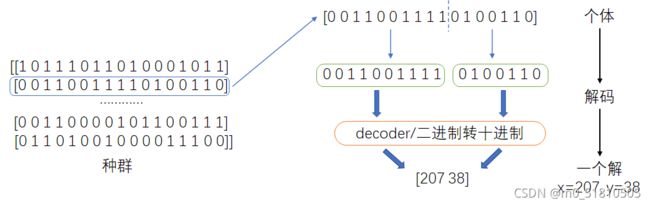
在实际的编程过程中,利用numpy并行化的特点,可以不必使用循环,直接用decoder处理矩阵,从种群矩阵zq直接计算排班方案矩阵plan(也就是解)。
decoder=lambda x:np.sum(np.power(2,np.arange(x.shape[-1]-1,-1,-1))*x, axis=1).reshape((-1,1)) #二进制转十进制
plan=np.hstack((decoder(zq[:,0:10]),decoder(zq[:,10:17]))) #将二进制编码解码为方案
代码图示:
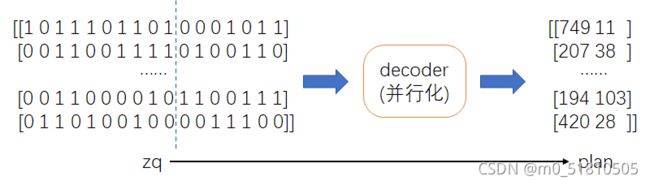
按照之前的思路,我们已经完成了第一步:在解空间中随机采样很多个解,接下来只要求出每一个方案的对应成本,选出部分成本较小的方案(也就是比较好的解)作为新种群,然后交叉变异迭代即可。但是在这之前,还有一个问题需要解决。
2.3 如何处理约束
显然,在这些随机采样得到的解当中,有部分方案无法将乘客载完(也就是不满足约束条件 20 x + 150 y ≥ N p a s s e n g e r s 20x+150y \geq N_{passengers} 20x+150y≥Npassengers)。如果不考虑约束,只是单纯的按照每个解求得的成本大小排序,那么最终必然收敛到 x = 0 , y = 0 x=0,y=0 x=0,y=0,根本无法求得可行解,更不用说最优解了。
因此,在选出较好解之前,必须先将不满足约束条件的解去掉,然后在剩下的解中再求成本,选出较好解。形象的讲,处理约束,相当于清理种群,先将种群中不符合约束条件的个体“杀死”。
代码实现是求一个kill矩阵,符合约束的位置是False,不合约束的位置是True。然后在种群中直接删除kill矩阵的对应位置。
kill=np.dot(plan,np.array([[20],[150]])) < cks #选出承载力小于乘客人数的方案
zq=np.delete(zq, np.where(kill), axis=0) #清理种群,清除所有不满足载客量要求的个体
plan=np.delete(plan, np.where(kill), axis=0) #清理种群,清除所有不满足载客量要求的个体
这样种群中剩下的解都是可行解了,接下来就可以进行第二步:挑出一些较好的解,也就是进行自然选择。
cost=np.dot(plan,np.array([[4],[15]])) #运输成本
select=np.max(cost)/cost #选择概率,成本越小,select概率越大
deleteindex=np.argsort(select.reshape(-1))[:int(select.shape[0]*0.7)] #贪心选择,对选择概率排序然后删除后0.7,保留前0.3
zq=np.delete(zq, deleteindex, axis=0) #进行选择,得到选择后的新种群
在代码中,我们先求出清理后的种群中每个个体的成本值矩阵cost,然后通过成本值(优化目标)求每个个体的选择概率矩阵select,越好的解(成本越小)被选择的概率就越大。
在这里为了简化问题,直接使用贪心策略选择个体,删除选择概率位于后百分之70的个体。这样便得到了自然选择后的种群,也就是挑出了一些比较好的解。留下来的个体作为父代进行第三步。
如果使用“轮盘赌”策略选择个体,那么处理约束时可以不用清理种群,只需要在计算选择概率时,减小不符合约束的个体的选择概率。
具体操作是:求kill矩阵变成求一个mask矩阵,符合约束的位置是1,不合约束的位置给一个很小的值。用成本求得选择概率后,乘这个mask即可。这样不合约束的个体,选择概率就会变得很小,等价于一个很差解,被自然选择淘汰。
接着在后面交叉那行使用np.random.choice(zq.shape[0],2,p=select.reshape(-1))来代替np.random.randint(0,zq.shape[0],(2))。select要除np.sum(select),处理成和为1的概率分布(贪心策略里没必要做这个处理,为了简单就不多写一行了)。
经过实际测试,在这个问题中轮盘赌策略收敛的很慢,大概要比贪心策略多迭代十倍才能收敛到最优解。同时choice函数的效率很低,同样的迭代次数下耗时要增加五六倍。
2.4 如何从较好解获得新的解
第二步完成,进入第三步:在较好的解附近采样,得到很多新解。具体是通过交叉与变异实现的。
在说明交叉与变异的意义前,先看看如何通过交叉与变异得到新的解,并进一步得到新的种群,完成遗传算法的一次迭代。
singlepoint_crossover=lambda x,po=random.randint(0,zq.shape[1]-3):np.hstack((x[0][:po],x[1][po:po+3],x[0][po+3:])) #单点交叉,输入[[编码1],[编码2]]
jc=np.array([singlepoint_crossover(zq[np.random.randint(0,zq.shape[0],(2))]).tolist() for o in range(700)]) #得到交叉的子群
by=np.abs(jc-(np.random.random(jc.shape)>0.95)) #变异,有0.05概率把对应位置值换一下
zq=np.vstack((zq,by)) #将父代与子代拼起来,得到新种群
交叉:
在这里,我使用了一个函数singlepoint_crossover,实现了最基本的单点交叉遗传。单点交叉遗传可以参考这篇文献:https://blog.csdn.net/ztf312/article/details/82793295
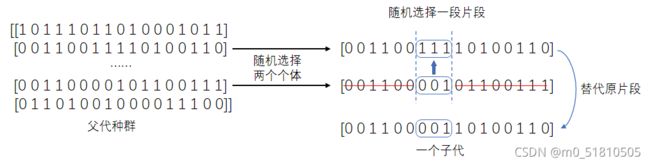
具体来讲,交叉就是在父代种群(自然选择后剩下的个体)中,随机选择两个个体作为父代,然后随机选择一段片段(代码中长为3),用其中一个父代的片段替换另一个父代的对应位置,就产生了一个子代个体。
在代码中,这个随机选择的过程进行了700次,产生了700个子代。这700个子代被拼成了一个700×17的矩阵jc(交叉),代表子代种群。
一次交叉的过程:
变异:
变异的实现比较简单,就是按照一定概率将子代的值改变。在代码中只对子代种群(也就是jc矩阵)进行变异,不对父代种群做任何处理。变异的策略如下:
b y ← a b s ( j c − 1 ) by \leftarrow abs(jc-1) by←abs(jc−1)
当原先值为1,变异后的值改变为0;原先值为0,变异后值改变为1。在代码中直接用jc减去一个随机0-1矩阵后取绝对值,其中的值有0.05的概率取1(也就是变异概率为0.05),完成变异。
拼接:
在通过交叉得到子代,对子代进行变异处理后,我们将父代与子代拼在一起,就得到了新的种群。拼接操作的意义是:让优秀的原先解不会丢失,又采样了周围的新解。
交叉变异拼接后,遗传算法的一次迭代完成,第三步完成。
将新的种群作为下一次迭代的初始种群,不断进行第四步:重复上述过程,最后就可以收敛到最优解了。
三、反思:真的是采样逼近吗 / 消融实验
在这个部分,我做了一些尝试与可视化,并试着解释一下遗传算法背后的道理。
这里所说的解的远近可以近似的理解为解向量的相似度,相似度高的解一般空间直线距离近,相似度低的一般空间直线距离远。
根据我的理解,遗传算法中出现了两种随机采样策略:
初始化种群——全局采样
交叉——附近采样
变异——全局采样
在运行下列每段代码前,首先调库并设置一些画图参数,这些参数能避免乱码并提高生成图片的分辨率:
import numpy as np
import matplotlib.pyplot as plt
import random
import time
plt.rcParams['font.sans-serif']='SimHei'
plt.rcParams['axes.unicode_minus']=False
plt.rcParams['savefig.dpi'] = 300
plt.rcParams['figure.dpi'] = 300
3.1 最优解和较好解的关系 / 遗传算法为什么可行
很多问题都拥有类似局部的凸优化的性质:更好的解位置在一群较好解的中间;越接近最优解、局部最优解的解越好;越接近最优解、局部最优解,较好解越密集,这有一些“近朱者赤”的意思。这个性质是遗传算法能够成功的关键。当解决的问题失去了这个性质后,遗传算法就退化为完全随机采样。
拿我们举例的整数规划问题来说,这个性质十分明显:例如飞机数越是增加,离最优解就越远,成本越高,这个解就越差;飞机数越小,就越是不能载满所有乘客,这个解就越是不符合约束。因此,当解距离最优解越近的时候,这个解的表现就越好。
例如在乘客数为5644时:
| 解[小飞机数, 大飞机数] | 成本增加率 | 无法搭载的乘客比例 | 主观评价 | 离最优解距离 Δ x 2 + Δ y 2 \sqrt{\Delta x^2+\Delta y^2} Δx2+Δy2 |
|---|---|---|---|---|
| [0, 38] | 0 | 0 | 最优解 | 0 |
| [5, 39] | 16% | 0 | 较好解 | 5.09 |
| [200, 50] | 172% | 0 | 较差解 | 200.3 |
| [5, 36] | -12% | 2% | 较好解 | 5.83 |
| [20, 10] | -40% | 66% | 较差解 | 32.8 |
拿一些其他博客的优化问题来说,一些典型的问题的解空间类似这样:
https://blog.csdn.net/google19890102/article/details/30044945
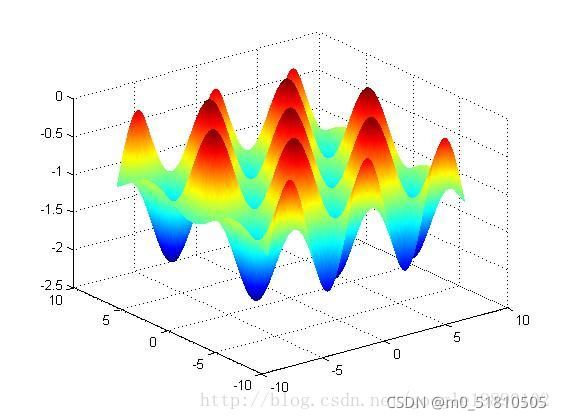
如果优化目标是函数值最小,那么很容易发现,距离最优解、局部最优解越近的解,用这个解计算的函数值就越小,这个解就越好。
反过来讲,如果我们找到了一群比较好的解,那么最优解或局部最优解大概率就在这些解的中间某处。
回想一下遗传算法的基本思路:在解空间中随机采样很多个解–>挑出一些较好的解–>在较好的解附近采样,得到很多新解–>重复进行上述第二、第三步,直到新解收敛到最优解。
我们发现,就这副图片的问题而言,如果在较好解附近采样新解,很有可能会得到更好的解;每次迭代都淘汰一些不那么好的解,到最后很可能会把一些局部最小值点淘汰(因为它们相对于最优解附近的解来说不够好)。像这样,通过采样——筛选好解——在好解周围继续采样——继续筛选,就可以慢慢的把解变得越来越好,这就是上文说的采样逼近。
这样一来,只要初始化时随机采样的解非常多,就有很大的概率能够覆盖在所有局部最优点周围,采样逼近就可以正常进行。同时,遗传算法的变异机制也保证了算法能够有机会随机探索全局的解。
但是,如果较好解与更好解之间没有了联系,遗传算法就只能靠全局随机采样来慢慢尝试最优解,这时候变异就担负起探索全局的作用。不过实现机制中会保留找到过的最好解,因此只要迭代的够多,甚至多到遍历整个解空间,那么遗传算法一样可以找到最优解。
3.2 为什么交叉能得到更优解
交叉实际上就是一种在较好解附近采样的策略。根据上文所述的问题的特性,这个采样策略自然可以得到更优解。那么交叉具体是怎样一个采样策略呢?
先看一看二进制编码下,交叉时发生了什么事情。
decoder=lambda x:np.sum(np.power(2,np.arange(x.shape[-1]-1,-1,-1))*x, axis=1).reshape((-1,1))
def crossover(length=3): #随机生成父代,产生所有的交叉结果,返回子代,交叉片段长3
fd=np.random.randint(0,2,(2,17))
zd=np.zeros((1,17))
for i in range(17-length):
zd1=np.hstack((fd[0][:i],fd[1][i:i+length],fd[0][i+length:])).reshape((1,-1))
zd2=np.hstack((fd[1][:i],fd[0][i:i+length],fd[1][i+length:])).reshape((1,-1))
zd=np.vstack((zd,zd1,zd2))
zd=np.delete(zd,0,axis=0)
return fd,zd
# 画图
fig,axs=plt.subplots(nrows=2,ncols=3)
for i in range(2):
for j in range(3):
fd,zd = crossover(length=3)
axs[i,j].scatter(decoder(zd[:,:10]), decoder(zd[:,10:]), alpha=0.8, s=5, label='子代个体')
axs[i,j].scatter(decoder(fd[:,:10]), decoder(fd[:,10:]), c='red', s=16, label='父代个体')
plt.legend()
在这段代码中,我们多次随机生成两个二进制编码父代,然后进行交叉,遍历了其所有可能得到的子代。然后将父代与子代解码为解(x, y),在图中画出。最后的结果如下图所示:
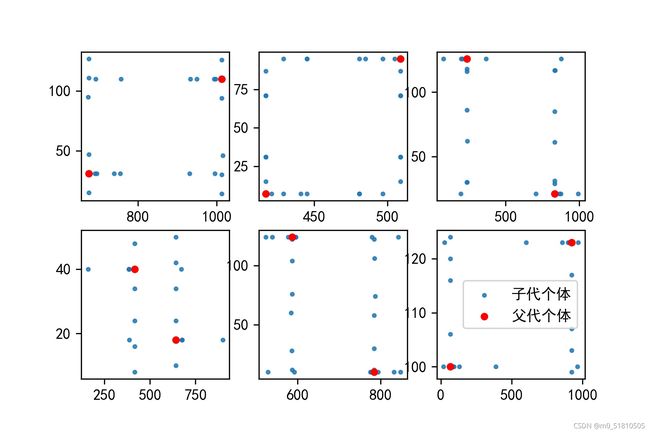
可以看出,父代产生的子代都分布在父代周围,给人的感觉就是在探索两个父代连线矩形的边与延长线,并且探索的大多是连线区域内的点,有较少的机会向外探索。探索的方式颇有“控制变量”的味道,即其中一个变量不变,另一个变量的值在两个父代值之间变化。
换句话说,子代的范围大多在这里面:
父 代 : [ x 1 , y 1 ] , [ x 2 , y 2 ] 子 代 : [ x , y ] ∣ x 1 < x < x 2 ; y 1 < y < y 2 父代:[x_1, y_1], [x_2, y_2] \\ 子代:[x,y]|\ x_1
这时候我们发现,交叉正是在两个较优解之间,按照“控制变量”的规则采样,生成新解。根据之前所说的问题特性:“更优解在较优解之间”,这个采样策略就可以采样到较优解间的更优解。
那么我们把多个父代放在一起,遍历它们所有的交叉结果,会发生什么呢?
fdzq=np.random.randint(0,2,(8,17))
zd=np.zeros((1,17))
for i,j in [(i,j) for i in range(8) for j in range(8)]:
fd=np.vstack((fdzq[i],fdzq[j]))
length=3
for o in range(17-length):
zd1=np.hstack((fd[0][:o],fd[1][o:o+length],fd[0][o+length:])).reshape((1,-1))
zd=np.vstack((zd,zd1))
zd=np.delete(zd,0,axis=0)
#画图
plt.scatter(decoder(zd[:,:10]), decoder(zd[:,10:]), alpha=0.8, s=5, label='子代个体')
plt.scatter(decoder(fdzq[:,:10]), decoder(fdzq[:,10:]), c='red', s=16, label='父代个体')
plt.legend()
在这段代码中,我们随机产生了8个父代,然后遍历了它们之间所有可能的交叉结果,并作图。运行结果如下:
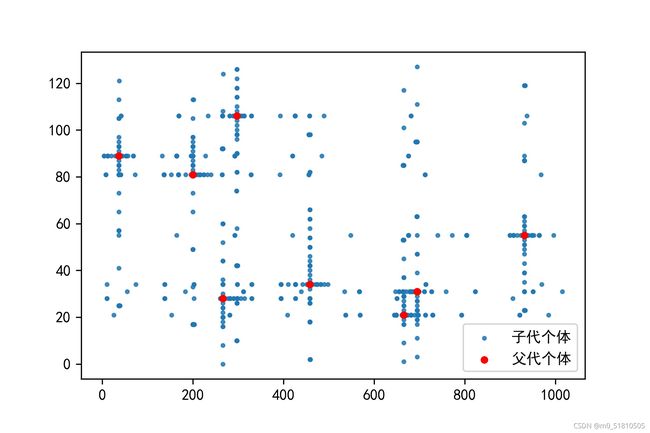
可以看到,在多个父代的时候,探索的区域大概就是以这些父代为交点的网状的区域。两个父代离得越近,在它们之间生成新子代的密度就越大。并且离父代越近,子代也就越密集。换句话说,交叉在探索新解的时候,父代越密集的地方,探索力度越大;越靠近父代,探索力度越大。
在这里,子代密度=采样密度=探索力度。
上文所说的问题特性之一是“越接近最优解、局部最优解,较好解越密集”。父代恰好是自然选择过的较好解,这样的采样策略正好是:对越可能出现更优解的地方,采样力度越大。因此交叉这个巧妙的技巧可以很好的探索更优解。
3.3 为什么交叉具有附近采样的特点
回忆一下二进制编码的方式:将小飞机数量用10位二进制表示,大飞机数量用7位二进制表示,然后将这两个二进制数拼成一个17维0-1向量。

二进制数在转十进制时有一个特点:二进制数越是高位的值改变,对十进制数的大小影响越大。也就是说二进制数的数量级主要取决于高位的数字是0还是1。
在交叉时,两个父代的片段进行交换。若交换的片段在低位,那么对十进制数的改变不大,子代值接近于原父代;若是出现在中间位置,由于没有影响到高位,因此改变的大小也有限,至少不会改变高位的数量级,子代值就在两个父代之间;若是出现在高位,那么被改变父代的值就会趋近于另一个父代,那么子代就趋于两个父代连成的矩形的另外两个交点上了。
不过无论如何,子代都不会远离父代好几个数量级。因此可以认为交叉拥有附近采样的特点。
因为编码比较长,而交换片段比较短,因此很难同时改变两个变量。这样交叉就出现了近乎“控制变量”的效果。
变异随机的改变某个位置的值,拥有在各个数量级上改变解大小的可能。因此变异具有全局采样的特点。
3.4 消融实验:你真的需要编码、变异与交叉吗
现在我们做减法,一点一点的将遗传算法的包装扒开,只保留随机采样、调整逼近的策略,看看让遗传算法拥有良好效果的是编码、变异与交叉本身其他的性质,还是随机采样的策略。
代码的运行结果放在3.4.4中统一展示。
3.4.1 二进制编码
我们先将二进制编码去掉。直接将方案 ( x , y ) (x,\ y) (x, y)作为个体,把方案矩阵plan作为初始种群,进行交叉与变异。具体的策略如下:
- 随机采样,生成一个1000×2的整数矩阵plan,其中第一列代表小飞机数量,取值[0,1024],第二列代表大飞机数量,取值[0,128],这与前面二进制编码飞机数范围是一样的。
- 交叉是简单的将两个父代的取值平均再取整,模拟在两个较优解之间采样的策略,并保证整数约束成立(相比于正常的交叉少了很多采样的随机性,这里是为了方便)。
- 变异是按一定概率,对其中某个值增减一个0到100间的随机数,并取绝对值保证约束成立。
去掉二进制编码的算法代码如下:
def get_plan_based_on_GA_without_encoding(cks):
plan=np.hstack((np.random.randint(0,1024,(1000,1)),np.random.randint(0,128,(1000,1))))
average_crossover=lambda x:np.floor(0.5*(x[0]+x[1]))
costlist=[]
for _ in range(20):
kill=np.dot(plan,np.array([[20],[150]])) < cks #选出承载力小于乘客人数的方案
plan=np.delete(plan, np.where(kill), axis=0) #清理种群,清除所有不满足载客量要求的个体
cost=np.dot(plan,np.array([[20*0.2],[150*0.1]])) #运输成本
select=np.max(cost)/cost #选择概率,成本越小,select概率越大
deleteindex=np.argsort(select.reshape(-1))[:int(select.shape[0]*0.9)] #贪心选择,对选择概率排序然后删除后0.7,保留前0.3
plan=np.delete(plan, deleteindex, axis=0) #进行选择,得到选择后的新种群
jc=np.array([average_crossover(plan[np.random.randint(0,plan.shape[0],(2))]).tolist() for o in range(700)])
by=np.abs(jc+(np.random.random(jc.shape)>0.8)*np.random.randint(-100,100,jc.shape))
plan=np.vstack((plan,by)) #将父代与子代拼起来,得到新种群
costlist.append(np.min(cost)) #记录最小开销
plt.plot(range(len(costlist)),costlist,label='不编码/整数编码')
return plan[np.argmin(cost)], np.min(cost)
这个算法是可以收敛的。
3.4.2 变异
既然去掉编码也可以成功,那么再大胆一些,把变异也去掉。
- 初始化种群的策略与3.4.1一样,随机采样plan矩阵作为初始种群。
- 由于去掉了变异,在这里交叉就得模拟原遗传算法,在两解附近采样时,产生一定的随机性。具体实现是:求两个父代的均值,随机增减一个0到10之间的整数,再取绝对值满足约束。
去掉二进制编码、变异的代码如下:
def get_plan_based_on_GA_without_by(cks):
plan=np.hstack((np.random.randint(0,1024,(1000,1)),np.random.randint(0,128,(1000,1))))
average_crossover=lambda x:np.abs(np.floor(0.5*(x[0]+x[1]))+np.random.randint(-10,10,(2))) #用随机扰动代替变异的作用
costlist=[]
for _ in range(20):
kill=np.dot(plan,np.array([[20],[150]])) < cks #选出承载力小于乘客人数的方案
plan=np.delete(plan, np.where(kill), axis=0) #清理种群,清除所有不满足载客量要求的个体
cost=np.dot(plan,np.array([[20*0.2],[150*0.1]])) #运输成本
select=np.max(cost)/cost #选择概率,成本越小,select概率越大
deleteindex=np.argsort(select.reshape(-1))[:int(select.shape[0]*0.9)] #贪心选择,对选择概率排序然后删除后0.7,保留前0.3
plan=np.delete(plan, deleteindex, axis=0) #进行选择,得到选择后的新种群
jc=np.array([average_crossover(plan[np.random.randint(0,plan.shape[0],(2))]).tolist() for o in range(700)])
plan=np.vstack((plan,jc)) #将父代与子代拼起来,得到新种群
costlist.append(np.min(cost)) #记录最小开销
plt.plot(range(len(costlist)),costlist,label='不编码不变异')
return plan[np.argmin(cost)], np.min(cost)
这个算法是可以收敛的。
3.4.3 交叉
既然又成功了,干脆把交叉的形式也去掉,直接按照最开始的思路:在较好的解附近采样,得到很多新解进行采样,具体如下:
- 初始化种群的策略与3.4.1、3.4.2一样,随机采样plan矩阵作为初始种群。
- 这次我们不取两个父本,只取一个父本,直接对其每个位置增减一个0到10之间的随机数,然后取绝对值保证约束。这就是最直接的“在较好解附近采样”。
去掉遗传算法所有包装:二进制编码、变异、交叉。纯粹的实现在较好解附近随机采样的策略,代码如下:
def get_plan_based_on_GA_without_jc(cks):
plan=np.hstack((np.random.randint(0,1024,(1000,1)),np.random.randint(0,128,(1000,1))))
random_neighbor_sampling=lambda x:np.abs(x+np.random.randint(-10,10,(2)))
costlist=[]
for _ in range(20):
kill=np.dot(plan,np.array([[20],[150]])) < cks #选出承载力小于乘客人数的方案
plan=np.delete(plan, np.where(kill), axis=0) #清理种群,清除所有不满足载客量要求的个体
cost=np.dot(plan,np.array([[20*0.2],[150*0.1]])) #运输成本
select=np.max(cost)/cost #选择概率,成本越小,select概率越大
deleteindex=np.argsort(select.reshape(-1))[:int(select.shape[0]*0.9)] #贪心选择,对选择概率排序然后删除后0.7,保留前0.3
plan=np.delete(plan, deleteindex, axis=0) #进行选择,得到选择后的新种群
new_plan=np.array([random_neighbor_sampling(plan[np.random.randint(0,plan.shape[0])]).tolist() for o in range(700)])
plan=np.vstack((plan,new_plan)) #将父代与子代拼起来,得到新种群
costlist.append(np.min(cost)) #记录最小开销
plt.plot(range(len(costlist)),costlist,label='在较优解附近随机采样')
return plan[np.argmin(cost)], np.min(cost)
这个算法是可以收敛的。
3.4.4 那么,还需要编码、交叉、变异吗
肯定需要,还是保持原汁原味的遗传算法最好。从3.2中我们就能看出,编码之后再交叉,采样的效果是非常好的,非常接近3.1中分析的问题的特性,更加合理。同时二进制编码下的变异随机性也更强,从感觉上来说比3.4.1中的变异策略更好。
之所以这几个消融实验可以成功,还是因为问题简单。当问题变得更加复杂,遗传算法会更加通用且可信。例如:在tsp问题、列车调度问题中,通过合理的编码能够很好的解决非结构化解的表示问题,并且让编码后的解有更好的“近朱者赤”的特性。在出现一些奇葩的解空间时,可能需要变异来进行全局采样,而不是仅靠附近采样就能收敛。总之,遗传算法相比消融实验的算法更加成熟、通用、可信度高。
进行消融实验,只是为了说明遗传算法的本质:采样逼近。
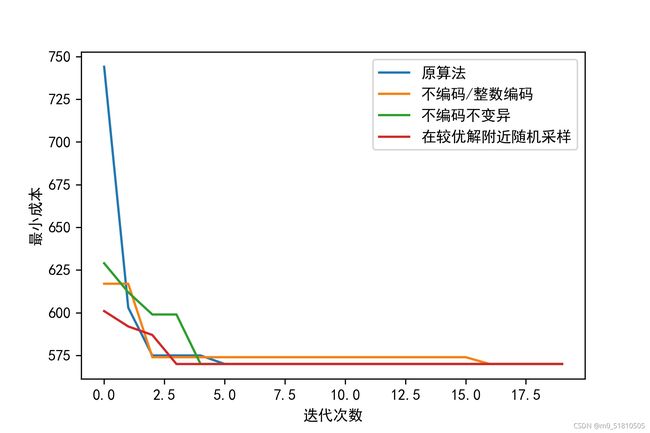
最后附上3.4中所有代码的运行结果。
start=time.time()
print(get_plan_based_on_GA(5644), time.time()-start) #原始算法
start=time.time()
print(get_plan_based_on_GA_without_encoding(5644), time.time()-start) #去掉二进制编码/整数编码
start=time.time()
print(get_plan_based_on_GA_without_by(5644), time.time()-start) #去掉变异
start=time.time()
print(get_plan_based_on_GA_without_jc(5644), time.time()-start) #去掉交叉/较优解附近随机采样
#画图
plt.xlabel('迭代次数')
plt.ylabel('最小成本')
plt.legend()
| 算法 | 方案[小飞机数量, 大飞机数量] | 最小成本 | 用时(s) |
|---|---|---|---|
| 原遗传算法 | [0, 38] | 570 | 0.257312536239624 |
| 不编码 | [0, 38] | 570 | 0.1894979476928711 |
| 不编码不变异 | [0, 38] | 570 | 0.3101644515991211 |
| 随机采样 | [0, 38] | 570 | 0.19550657272338867 |
水平所限,一些认识可能偏差或者错误,一些表达可能啰嗦而难懂,或者不清晰。希望各位大佬不吝赐教。
完结撒花
完稿于2021.11.20 1:49