MATALB大数的加减乘除幂运算
MATALB大数的加减乘除幂运算
- 一、基本原理
- 二、MATLAB简单实现
-
-
- 1. 加(+)
- 2. 减(-)
- 3. 乘(*)
- 4. 除(/)
- 5. 幂(^)
-
- 三、测试
- 四、关于优化
- 五、其他
by HPC_ZY
最近需要做大数计算,且要求结果精度与原始数据一致(不能使用科学计数等近似解)。所以总结分享一些“超大正整数的基本运算方法”,如加、减、乘、除、幂等
一、基本原理
uint32(unsigned int)型可表示的最大数为 ( 2 32 − 1 ) (2^{32}-1) (232−1),uint64(unsigned long long)型可表示的最大数为 ( 2 64 − 1 ) (2^{64}-1) (264−1),超过这样的数就没法直接计算了。
但是我们知道加减乘除的本质还是按位计算,所以我们可以将大数拆分为多个小位数。
根据这个原理最合适的就是使用字符串的形式,这样就将上限从最大数据类型变成了计算机最大内存。
下面我们就来研究字符串格式的加减乘除,首先分享MATLAB中的实现方法,然后改写成C。
注:本文仅研究正整数,暂不涉及负数与小数
二、MATLAB简单实现
1. 加(+)
任意大数相加,主要原理:
1)按位相加
2)满十进一
%% 大数加(输入为字符串格式)
function out = OLNadd(a,b)
% 转数字矩阵(为了逻辑方便,我们将数字反序)
mata = a(end:-1:1)-'0';
matb = b(end:-1:1)-'0';
% 计算位数
la = length(a);
lb = length(b);
% 初始化
if la>=lb
digitStart = lb;
matout = [mata,0];
mattmp = matb;
else
digitStart = la;
matout = [matb,0];
mattmp = mata;
end
% 循环求解
for k = digitStart:-1:1
% 位求和,满十进一
tmp = matout(k)+mattmp(k);
if tmp<10
matout(k) = tmp;
else
matout(k) = tmp-10;
matout(k+1) = matout(k+1)+1;
end
end
% 转字符
out = char(matout(end:-1:1)+'0');
if out(1) == '0'
out(1) = [];
end
end
2. 减(-)
任意大数相减,主要原理:
1)比较大小,以大减小
2)符号由大小关系决定
3)按位相减
4)不够向前借位
%% 大数减(输入为字符串格式)
function out = OLNsub(a,b)
% 转数字矩阵(为了逻辑方便,我们将数字反序)
mata = a(end:-1:1)-'0';
matb = b(end:-1:1)-'0';
% 计算位数
la = length(a);
lb = length(b);
% 初始化
isEqual = 0;
if la>lb % 默认用大的减小的(正负号由大小关系决定)
digitEnd = lb;
matout = [mata,0];
mattmp = matb;
flag = 1; % 结果为正
elseif la<lb
digitEnd = la;
matout = [matb,0];
mattmp = mata;
flag = 0; % 结果为负
else
% 对比第一个不相等的位数,谁大谁小
idx = find(a~=b,1);
if ~isempty(idx)
if a(idx)>b(idx)
digitEnd = lb;
matout = [mata,0];
mattmp = matb;
flag = 1; % 结果为正
else
digitEnd = la;
matout = [matb,0];
mattmp = mata;
flag = 0; % 结果为负
end
else % 如果为空,说明两个数完全一致
isEqual = 1;
end
end
if ~isEqual
% 循环求解
for k = 1:digitEnd
% 位求差,不足借一
if matout(k)>=mattmp(k)
matout(k) = matout(k)-mattmp(k);
else
matout(k) = 10+matout(k)-mattmp(k);
borrow = 1;
while 1 % 不够减时往前借,直到借到为止。
if matout(k+borrow)>=1 % 够借ok
matout(k+borrow) = matout(k+borrow)-1;
break
else % 不够,再往前
matout(k+borrow) = 10+matout(k+borrow)-1;
borrow = borrow+1;
end
end
end
end
% 转字符
out = char(matout(end:-1:1)+'0');
while out(1)=='0'
out(1) = [];
end
if ~flag
out = ['-',out];
end
else
out = '0';
end
end
3. 乘(*)
任意大数相乘,主要原理:
1)按位求积
2)结果累加
%% 大数乘(输入为字符串格式)
function out = OLNmult(a,b)
% 转数字矩阵(为了逻辑方便,我们将数字反序)
mata = a(end:-1:1)-'0';
matb = b(end:-1:1)-'0';
% 计算位数
la = length(a);
lb = length(b);
% 初始化
matout = zeros(1,la+lb);
% 循环求解
for i = 1:la
if mata(i)==0
continue
end
for j = 1:lb
if matb(j)==0
continue
end
% 位求积,分高低位
valtmp = mata(i)*matb(j);
valup = floor(valtmp/10);
vallow = valtmp-valup*10;
% 低位求和
idx = i+j-1;
val = matout(idx)+vallow;
if val<10
matout(idx) = val;
else
matout(idx) = val-10;
matout(idx+1) = matout(idx+1)+1;
end
% 求高位
idx = i+j;
val = matout(idx)+valup;
if val<10
matout(idx) = val;
else
matout(idx) = val-10;
matout(idx+1) = matout(idx+1)+1;
end
end
end
% 转字符
out = char(matout(end:-1:1)+'0');
while out(1)=='0'
out(1) = [];
end
if ~flag
out = ['-',out];
end
end
4. 除(/)
被除数任意大,除数 < 99999999 <99999999 <99999999。
(原因是在除法中,被除数符合分配律,除数不符合。对于超过类型允许的除数,我不知道怎么处理。所以采取的思路是将被除数拆分为类型允许的大小,即 < 2 32 − 1 = 4294967295 <2^{32}-1 = 4294967295 <232−1=4294967295(十位数),拆分的被除数最大只能为 999999999 999999999 999999999(九位数),进而得到除数最多为 99999999 99999999 99999999(八位数),主要原理:
1)按位求商,不足移位(即用最高位/除数,不够除则用最高两位,还不够用最高三位,以此类推)
2)高位余数,加至低位
%% 大数除(输入为字符串格式)
function [out,remainder] = OLNdiv(a,b)
% 转数字矩阵(为了逻辑方便,我们将数字反序)
mata = a(end:-1:1)-'0';
matb = b(end:-1:1)-'0';
% 计算位数
la = length(a);
lb = length(b);
% 转数字(按四位分组)
numa = mata(end:-1:1);
numb = 0;
for k = 1:lb
numb = numb+matb(k)*10^(k-1);
end
% 分组除保存结果
res = zeros(1,la); %
remainder = 0; % 每次计算的余数
for i = 1:la
divisor = numa(i)+remainder*10; % 被除数 = 上一组的余数*10000+这一组
remainder = rem(divisor,numb);
res(i) = (divisor-remainder)/numb;
end
% 转字符
remainder = num2str(remainder);
out = char(res+'0');
while out(1)=='0'
out(1) = [];
end
if ~flag
out = ['-',out];
end
end
5. 幂(^)
底数指数任意大。主要原理:
1)循环大数乘
%% 大数幂(输入为字符串格式)
function out = OLNpow(a,b)
% 转数字矩阵(为了逻辑方便,我们将数字反序)
matb = b(end:-1:1)-'0';
% 计算位数
lb = length(matb);
% 初始化
n = -1;
for k = 1:lb
n = n+matb(k)*10^(k-1);
end
% 循环乘(直接利用大数乘法,偷下懒)
tmp = a;
for k = 1:n
tmp = OLNmult(tmp,a);
end
out = tmp;
end
三、测试
- 准确性测试
首先测试各个算法结果是否正确,我们用int64能支持的数字进行,如下
%% 加
ca = '68924355';
cb = '411533';
cc = OLNadd(ca,cb); % 字符计算
nc = str2double(ca)+str2double(cb); % 数字计算
disp('加:')
disp([ca,' + ', cb,' = ',cc])
disp(['标准答案 = ',num2str(nc)])
disp(' ')
%% 减
% 基本测试
ca = '985355';
cb = '411533';
cc = OLNsub(ca,cb); % 字符计算
nc = str2double(ca)-str2double(cb); % 数字计算
disp('减-基本测试:');
disp([ca,' - ', cb,' = ',cc])
disp(['标准答案 = ',num2str(nc)])
disp(' ')
% 小减大测试
ca = '85355';
cb = '411533';
cc = OLNsub(ca,cb); % 字符计算
nc = str2double(ca)-str2double(cb); % 数字计算
disp('减-小减大测试:')
disp([ca,' - ', cb,' = ',cc])
disp(['标准答案 = ',num2str(nc)])
disp(' ')
% 借位测试
ca = '100000';
cb = '1';
cc = OLNsub(ca,cb); % 字符计算
nc = str2double(ca)-str2double(cb); % 数字计算
disp('减-借位测试:')
disp([ca,' - ', cb,' = ',cc])
disp(['标准答案 = ',num2str(nc)])
disp(' ')
%% 乘
ca = '996655';
cb = '872233';
cc = OLNmult(ca,cb); % 字符计算
nc = str2double(ca)*str2double(cb); % 数字计算
disp('乘:')
disp([ca,' * ', cb,' = ',cc])
disp(['标准答案 = ',num2str(nc)])
disp(' ')
%% 除
% 整除测试
ca = '869315380615';
cb = '872233';
[cc,cr] = OLNdiv(ca,cb); % 字符计算
nr = rem(str2double(ca),str2double(cb)); % 余数计算
nc = (str2double(ca)-nr)/str2double(cb); % 数字计算
disp('除-整除测试:')
disp([ca,' / ', cb,' = ', cc,' 余 ',cr])
disp(['标准答案 = ',num2str(nc),' 余 ',num2str(nr)])
disp(' ')
% 非整除测试
ca = '88772211996655';
cb = '872233';
[cc,cr] = OLNdiv(ca,cb); % 字符计算
nr = rem(str2double(ca),str2double(cb)); % 余数计算
nc = (str2double(ca)-nr)/str2double(cb); % 数字计算
disp('除-非整除测试:')
disp([ca,' / ', cb,' = ', cc,' 余 ',cr])
disp(['标准答案 = ',num2str(nc),' 余 ',num2str(nr)])
disp(' ')
%% 幂
ca = '16';
cb = '11';
cc = OLNpow(ca,cb); % 字符计算
nc = str2double(ca)^str2double(cb); % 数字计算
disp('幂:')
disp([ca,' ^ ', cb,' = ',cc])
disp(['标准答案 = ',num2str(nc)])
disp(' ')
结果如下,完全一致,接下来可以放心测试大数
- 大数测试
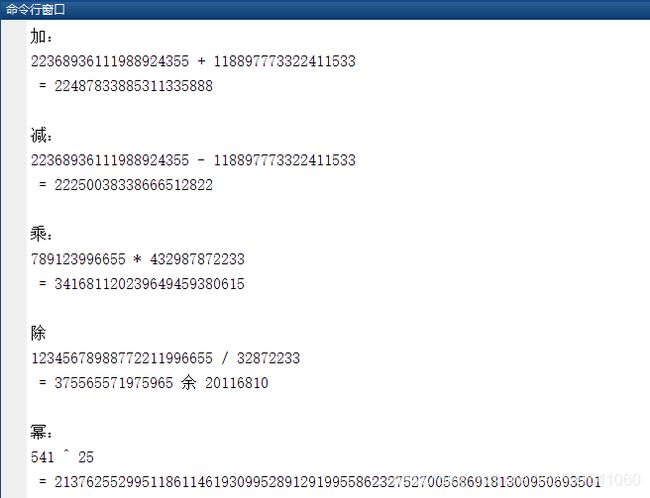
使用超大数字进行测试
%% 加
ca = '22368936111988924355';
cb = '118897773322411533';
cc = OLNadd(ca,cb); % 字符计算
disp('加:')
disp([ca,' + ', cb]),disp([' = ',cc])
disp(' ')
%% 减
ca = '22368936111988924355';
cb = '118897773322411533';
cc = OLNsub(ca,cb); % 字符计算
disp('减:');
disp([ca,' - ', cb]),disp([' = ',cc])
disp(' ')
%% 乘
ca = '789123996655';
cb = '432987872233';
cc = OLNmult(ca,cb); % 字符计算
disp('乘:')
disp([ca,' * ', cb]),disp([' = ',cc])
disp(' ')
%% 除
ca = '12345678988772211996655';
cb = '32872233';
[cc,cr] = OLNdiv(ca,cb); % 字符计算
disp('除')
disp([ca,' / ', cb]),disp([' = ',cc,' 余 ',cr])
disp(' ')
%% 幂
ca = '541';
cb = '25';
cc = OLNpow(ca,cb); % 字符计算
disp('幂:')
disp([ca,' ^ ', cb]),disp([' = ',cc])
disp(' ')
四、关于优化
- 为了理解方便所以函数写法有累赘的地方,自己使用时可合理优化。
- 有大佬提出,加减乘除可以在二进制计算中完成。
- 关于幂运算中,指数太大计算时间会爆表,可以改写为快速幂方法。
- 我没有加入判断语句,即使输入的不是数字还是会计算,可以加上。
- 可以对输入加上符号,这样就能进行负数计算。
- 关于小数计算,加减乘很简单,只要判断小数点位置即可。除法则需要在此基础上加上计算精度(小数后保留几位)。关于幂,底数为小数类似乘法,但指数为小数就要配合开方。
五、其他
1、该方法的C实现可看另一篇文章《C/C++大数的加减乘除幂运算》。撰写中……
2、函数与测试代码文中已全部公开,如果嫌懒得复制且已开通会员,可以在这里下载demo