mlr3实战 | 基于临床参数的肝病患者分类(7种常用的机器学习方法)
序言
下面的例子是慕尼黑大学机器学习入门讲座的一部分内容。该项目的目标是为手头的问题创建并比较一个或几个机器学习管道，同时进行探索性分析并对结果进行阐述。
准备
mlr3的详细指南见：
mlr3 book (https://mlr3book.mlr-org.com/index.html)
## 安装与加载所需包
install.packages('mlr3verse')
install.packages('DataExplorer')
install.packages('gridExtra')
library(mlr3verse)
library(dplyr)
library(tidyr)
library(DataExplorer)
library(ggplot2)
library(gridExtra)用一个固定的种子来初始化随机数发生器，以保证可重复性，并减少记录器的冗长性，以保持输出的清晰表现。
set.seed(7832)
lgr::get_logger("mlr3")$set_threshold("warn")
lgr::get_logger("bbotk")$set_threshold("warn")在这个示例中，作者研究了机器学习算法和学习器在肝病检测方面的具体应用。因此，该任务是一个二元分类任务，根据一些常见的诊断测量结果预测病人是否患有肝病。
示例数据及代码领取：点赞、在看本文，分享至朋友圈集赞10个并保留30分钟。截图发送微信号：mzbj0002，或扫描下面二维码。2022年VIP会员免费领取。
木舟笔记2022年度VIP企划
权益：
2022年度木舟笔记所有推文示例数据及代码(含大部分2021年)。
木舟笔记科研交流群。
半价购买
跟着Cell学作图系列合集(免费教程+代码领取)|跟着Cell学作图系列合集。
收费：
99￥/人。可添加微信：mzbj0002 转账，或直接在文末打赏。
印度肝病数据
# Importing data
data("ilpd", package = "mlr3data")它包含了在印度的安得拉邦东北部收集的583名患者的数据。根据病人是否有肝病，观察结果被分为两类。除了我们的目标变量外，还提供了十个主要是数字的特征。为了更详细地描述这些特征，下表列出了数据集中的变量。
| Variable | Description |
|---|---|
| age | Age of the patient (all patients above 89 are labelled as 90 |
| gender | Sex of the patient (1 = female, 0 = male) |
| total_bilirubin | Total serum bilirubin (in mg/dL) |
| direct_bilirubin | Direct bilirubin level (in mg/dL) |
| alkaline_phosphatase | Serum alkaline phosphatase level (in U/L) |
| alanine_transaminase | Serum alanine transaminase level (in U/L) |
| aspartate_transaminase | Serum aspartate transaminase level (in U/L) |
| total_protein | Total serum protein (in g/dL) |
| albumin | Serum albumin level (in g/dL) |
| albumin_globulin_ratio | Albumin-to-globulin ratio |
| diseased | Target variable (1 = liver disease, 0 = no liver disease) |
显然，一些测量值是其它变量的一部分。例如，血清总胆红素是直接胆红素和间接胆红素水平的总和；而白蛋白的数量则用于计算血清总蛋白以及白蛋白-球蛋白比率的数值。因此，一些特征是彼此高度相关的，下面会进行处理。
数据预处理
单变量分布
接下来，研究每个变量的单变量分布。从目标变量和唯一的离散特征--性别开始，它们都是二元变量的。
## 所有离散变量的频率分布
plot_bar(ilpd,ggtheme = theme_bw())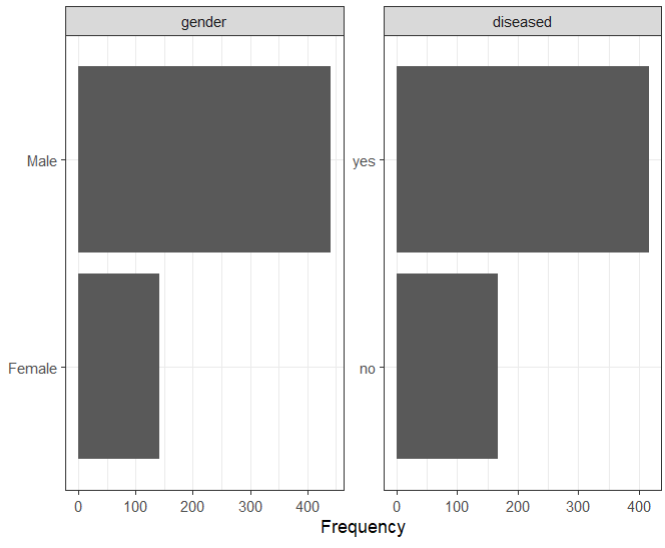
image-20220408132411502
可以看到，目标变量（即肝病与非肝病患者）的分布是相当不平衡的，如柱状图所示：有肝病和无肝病的患者数量分别为416和167。一个类别的代表性不足，可能会使ML模型的性能恶化。为了研究这个问题，作者还在一个数据集上拟合了模型，在这个数据集上，随机地对少数人类别进行了过度抽样，结果是一个完全平衡的数据集。此外，我们还应用了分层抽样，以确保在交叉验证过程中保持各类的比例。唯一的离散特征gender也是相当不平衡的。
## 查看所有连续变量的频率分布直方图
plot_histogram(ilpd,ggtheme = theme_mlr3())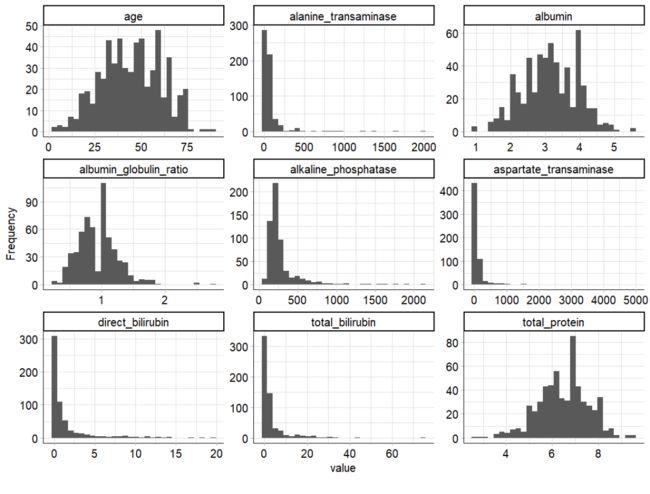
histogram
可以看到，一些指标特征是极度右偏的，包含几个极端值。为了减少离群值的影响，并且由于一些模型假设了特征的正态性，我们对这些变量进行了log转换。
特征分组
为了描绘目标和特征之间的关系，我们按类别分析了特征的分布情况。首先，我们研究了离散特征性别。
plot_bar(ilpd,by = 'diseased',ggtheme = theme_mlr3())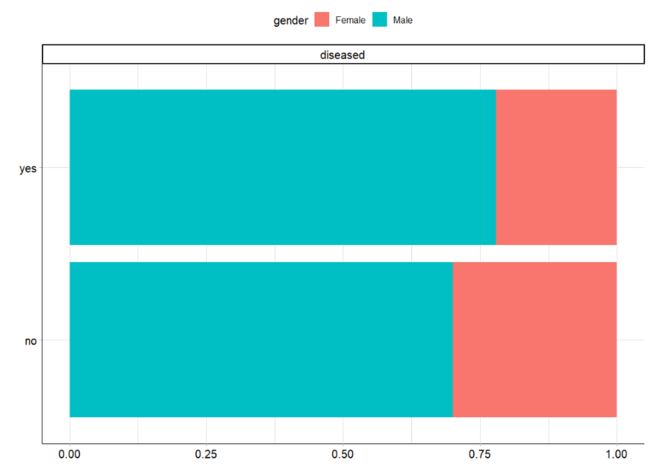
在 "疾病 "类中，男性的比例略高，但总体而言，差异不大。除此之外，正如我们之前提到的，在两个类别中都可以观察到性别不平衡的现象。
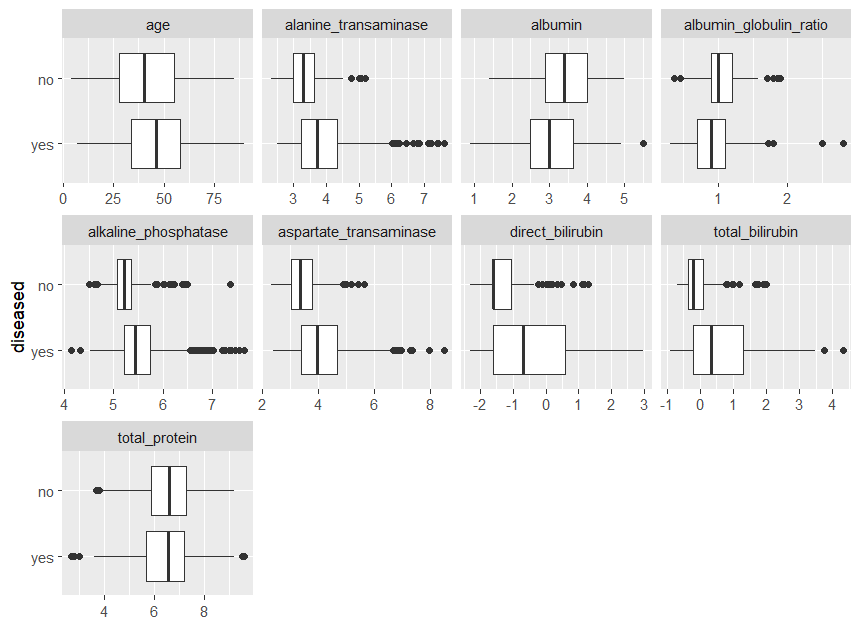
为了看到连续特征的差异，我们比较了以下的boxplots，其中右偏的特征还没有进行对数转换。
## View bivariate continuous distribution based on `diseased`
plot_boxplot(ilpd,by = 'diseased')
可以看到除了total_protein，对于每一个特征，我们都得到了两个类的中位值之间的差异。值得注意的是，在强右偏的特征中，"疾病 "类包含的极端值远远多于 "无疾病 "类，这可能是因为其规模较大。
从下面的图中可以看出，这种影响在对数转换后会被削弱。此外，这些特征在 "疾病 "类中的分散性更大，正如箱线图的长度所示。总的来说，这些特征似乎与目标相关，所以将它们用于这项任务并建立它们与目标的关系模型是有意义的。
对部分特征进行log转换
ilpd_log = ilpd %>%
mutate(
# Log for features with skewed distributions
alanine_transaminase = log(alanine_transaminase),
total_bilirubin =log(total_bilirubin),
alkaline_phosphatase = log(alkaline_phosphatase),
aspartate_transaminase = log(aspartate_transaminase),
direct_bilirubin = log(direct_bilirubin)
)
plot_histogram(ilpd_log,ggtheme = theme_mlr3(),ncol = 3)
plot_boxplot(ilpd_log,by = 'diseased')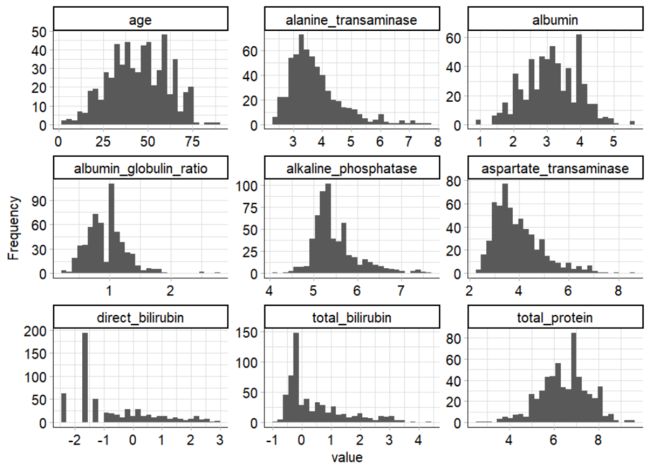
可以看到log转换后的数据分布改善了许多。
相关分析
正如我们在数据描述中提到的，有些特征是由另一个特征间接测量的。这表明它们是高度相关的。我们要比较的一些模型假设是独立的特征，或者有多重共线性的问题。因此，我们检查了特征之间的相关性。
plot_correlation(ilpd)
可以看到，其中四对有非常高的相关系数。看一下这些特征，很明显它们是相互影响的。由于模型的复杂性应该最小化，并且由于多重共线性的考虑，我们决定每对特征中只取一个。在决定保留哪些特征时，我们选择了那些关于肝病的更具体和相关的特征。因此，我们选择了白蛋白，而不是白蛋白和球蛋白的比例，也不是蛋白质的总量。同样的观点也适用于使用直接胆红素的量而不是总胆红素。关于天门冬氨酸转氨酶和丙氨酸转氨酶，我们没有注意到这两个特征的数据有任何根本性的差异，所以我们任意选择了天冬氨酸转氨酶。
最终数据集
## Reducing, transforming and scaling dataset
ilpd = ilpd %>%
select(-total_bilirubin, -alanine_transaminase, -total_protein,
-albumin_globulin_ratio) %>%
mutate(
# Recode gender
gender = as.numeric(ifelse(gender == "Female", 1, 0)),
# Remove labels for class
diseased = factor(ifelse(diseased == "yes", 1, 0)),
# Log for features with skewed distributions
alkaline_phosphatase = log(alkaline_phosphatase),
aspartate_transaminase = log(aspartate_transaminase),
direct_bilirubin = log(direct_bilirubin)
)
## 标准化
po_scale = po("scale")
po_scale$param_set$values$affect_columns =
selector_name(c("age", "direct_bilirubin", "alkaline_phosphatase",
"aspartate_transaminase", "albumin"))
task_liver = as_task_classif(ilpd_m, target = "diseased", positive = "1")
ilpd_f = po_scale$train(list(task_liver))[[1]]$data()最后，我们对所有的连续变量特征进行了标准化，这对k-NN模型尤其重要。下表显示了最终的数据集和我们应用的转换。注意：与对数或其他转换不同，缩放取决于数据本身。在数据被分割之前对数据进行缩放会导致数据泄露(详见：Nature Reviews Genetics | 在基因组学中应用机器学习的常见陷阱），因为训练集和测试集的信息是共享的。由于数据泄露会导致更高的性能，缩放应该总是单独应用于ML工作流程所引起的每个数据分割。因此，我们强烈建议在这种情况下使用PipeOpScale。
学习器和调参
首先，我们需要定义一个task，其中包含最终的数据集和一些元信息。此外，我们还需要指定正类，因为软件包默认将第一个正类作为正类。正类的指定对后面的评估有影响。
## Task definition
task_liver = as_task_classif(ilpd_f, target = "diseased", positive = "1")下面我们将对logistic regression, linear discriminant analysis (LDA), quadratic discriminant analysis (QDA), naive Bayes, k-nearest neighbour (k-NN), classification trees (CART) and random forest的二元分类目标进行评估。
# detect overfitting
install.packages('e1071')
install.packages('kknn')
learners = list(
learner_logreg = lrn("classif.log_reg", predict_type = "prob",
predict_sets = c("train", "test")),
learner_lda = lrn("classif.lda", predict_type = "prob",
predict_sets = c("train", "test")),
learner_qda = lrn("classif.qda", predict_type = "prob",
predict_sets = c("train", "test")),
learner_nb = lrn("classif.naive_bayes", predict_type = "prob",
predict_sets = c("train", "test")),
learner_knn = lrn("classif.kknn", scale = FALSE,
predict_type = "prob"),
learner_rpart = lrn("classif.rpart",
predict_type = "prob"),
learner_rf = lrn("classif.ranger", num.trees = 1000,
predict_type = "prob")
)调参
为了找到最佳的超参数，我们使用随机搜索来更好地覆盖超参数空间。我们定义了要调整的超参数。我们只调整了k-NN、CART和随机森林的超参数，因为其他方法有很强的假设，并作为基线。
对于k-NN，我们选择3作为k（邻居数量）的下限，50作为上限。太小的k会导致过度拟合。我们还尝试了不同的距离测量方法（Manhattan distance为1, Euclidean distance为2）和内核。对于CART，我们调整了超参数cp（复杂度参数）和minsplit（为了尝试分割，一个节点中的最小观察数）。cp控制了tree的大小：小的值会导致过拟合，而大的值会导致欠拟合。我们还调整了随机森林的终端节点的最小尺寸和每次分裂时随机抽样作为候选变量的数量（从1到特征数）的参数。
tune_ps_knn = ps(
k = p_int(lower = 3, upper = 50), # Number of neighbors considered
distance = p_dbl(lower = 1, upper = 3),
kernel = p_fct(levels = c("rectangular", "gaussian", "rank", "optimal"))
)
tune_ps_rpart = ps(
# Minimum number of observations that must exist in a node in order for a
# split to be attempted
minsplit = p_int(lower = 10, upper = 40),
cp = p_dbl(lower = 0.001, upper = 0.1) # Complexity parameter
)
tune_ps_rf = ps(
# Minimum size of terminal nodes
min.node.size = p_int(lower = 10, upper = 50),
# Number of variables randomly sampled as candidates at each split
mtry = p_int(lower = 1, upper = 6)
)下一步是将mlr3tuning中的AutoTuner实例化。我们对嵌套重采样的内循环采用了5-fold交叉验证法。评价次数被设定为100次作为停止标准。我们使用AUC作为评价指标，。
如前所述，由于目标类别不平衡，我们选择了完美平衡类。通过使用mlr3pipelines，我们可以在以后应用基准函数。
# Oversampling minority class to get perfectly balanced classes
po_over = po("classbalancing", id = "oversample", adjust = "minor",
reference = "minor", shuffle = FALSE, ratio = 416/167)
table(po_over$train(list(task_liver))$output$truth()) # Check class balance
# Learners with balanced/oversampled data
learners_bal = lapply(learners, function(x) {
GraphLearner$new(po_scale %>>% po_over %>>% x)
})
lapply(learners_bal, function(x) x$predict_sets = c("train", "test"))模型拟合和基准设定
在定义了学习器、选择了嵌套重采样的内部方法和设置了调整器之后，我们开始选择外部重采样方法。我们选择了分层的5倍交叉验证法，以保持目标变量的分布，不受过度采样的影响。然而，事实证明，没有分层的正常交叉验证法也会产生非常相似的结果。
# 5-fold cross-validation
resampling_outer = rsmp(id = "cv", .key = "cv", folds = 5L)
# Stratification
task_liver$col_roles$stratum = task_liver$target_names为了对不同的学习器进行排名，并最终决定哪一个最适合手头的任务，我们使用了**基准测试(benchmarking)**。下面的代码块执行了我们对所有学习者的基准测试。
design = benchmark_grid(
tasks = task_liver,
learners = c(learners, learners_bal),
resamplings = resampling_outer
)
bmr = benchmark(design, store_models = FALSE) ## 耗时较长如上所述，我们选择了分层的5折交叉验证法。这意味着性能被确定为五个模型评估的平均值，train-test-split为80%和20%。此外，性能指标的选择对于不同学习器的排名至关重要。虽然每一个都有其特定的使用情况，但我们选择了AUC，一个同时考虑了敏感性和特异性的性能指标，我们也使用它来进行超参数调整。
我们首先通过AUC对所有学习者进行了比较，包括有无超采样，以及训练和测试数据。
measures = list(
msr("classif.auc", predict_sets = "train", id = "auc_train"),
msr("classif.auc", id = "auc_test")
)
tab = bmr2$aggregate(measures)
tab_1 = tab[,c('learner_id','auc_train','auc_test')]
print(tab_1)> print(tab_1)
learner_id auc_train auc_test
1: classif.log_reg 0.7548382 0.7485372
2: classif.lda 0.7546522 0.7487159
3: classif.qda 0.7683438 0.7441634
4: classif.naive_bayes 0.7539374 0.7498427
5: classif.kknn.tuned 0.8652143 0.7150679
6: classif.rpart.tuned 0.7988561 0.6847818
7: classif.ranger.tuned 0.9871615 0.7426650
8: scale.oversample.classif.log_reg 0.7540066 0.7497002
9: scale.oversample.classif.lda 0.7537952 0.7489675
10: scale.oversample.classif.qda 0.7679012 0.7481963
11: scale.oversample.classif.naive_bayes 0.7536208 0.7503436
12: scale.oversample.classif.kknn.tuned 0.9982251 0.6870297
13: scale.oversample.classif.rpart.tuned 0.8903927 0.6231100
14: scale.oversample.classif.ranger.tuned 1.0000000 0.7409655从上面的结果可以看出，无论是否应用了超采样，逻辑回归、LDA、QDA和NB在训练和测试数据上的表现非常相似。另一方面，k-NN、CART和随机森林在训练数据上的预测效果要好得多，这表明过度拟合。
此外，过度取样使所有学习器的AUC性能几乎没有变化。
下面的箱线图展示了所有学习器的5折交叉验证的AUC性能。
# boxplot of AUC values across the 5 folds
autoplot(bmr2, measure = msr("classif.auc"))
image-20220408223435031
autoplot(bmr2,type = "roc")+
scale_color_discrete() +
theme_bw()
image-20220410085535155
随后，输出每个学习器的敏感性、特异性、假阴性率（FNR）和假阳性率（FPR）。
tab2 = bmr2$aggregate(msrs(c('classif.auc', 'classif.sensitivity','classif.specificity',
'classif.fnr', 'classif.fpr')))
tab2 = tab2[,c('learner_id','classif.auc','classif.sensitivity','classif.specificity',
'classif.fnr', 'classif.fpr')]
print(tab2)> print(tab2)
learner_id classif.auc classif.sensitivity
1: classif.log_reg 0.7485372 0.8917097
2: classif.lda 0.7487159 0.9037005
3: classif.qda 0.7441634 0.6779116
4: classif.naive_bayes 0.7498427 0.6250430
5: classif.kknn.tuned 0.7180074 0.8509180
6: classif.rpart.tuned 0.6987046 0.8679289
7: classif.ranger.tuned 0.7506405 0.9447504
8: scale.oversample.classif.log_reg 0.7475678 0.6008893
9: scale.oversample.classif.lda 0.7489090 0.5841652
10: scale.oversample.classif.qda 0.7431096 0.5529547
11: scale.oversample.classif.naive_bayes 0.7494055 0.5505164
12: scale.oversample.classif.kknn.tuned 0.6924480 0.6948078
13: scale.oversample.classif.rpart.tuned 0.6753005 0.7090075
14: scale.oversample.classif.ranger.tuned 0.7393948 0.7427424
classif.specificity classif.fnr classif.fpr
1: 0.2516934 0.10829030 0.7483066
2: 0.1855615 0.09629948 0.8144385
3: 0.6946524 0.32208835 0.3053476
4: 0.7488414 0.37495697 0.2511586
5: 0.2581105 0.14908204 0.7418895
6: 0.3108734 0.13207114 0.6891266
7: 0.1554367 0.05524957 0.8445633
8: 0.7663102 0.39911073 0.2336898
9: 0.8023173 0.41583477 0.1976827
10: 0.8139037 0.44704532 0.1860963
11: 0.8381462 0.44948365 0.1618538
12: 0.5811052 0.30519220 0.4188948
13: 0.5449198 0.29099254 0.4550802
14: 0.5509804 0.25725760 0.4490196事实证明，在没有超采样的情况下，逻辑回归、LDA、k-NN、CART和随机森林在敏感性方面得分很高，而在特异性方面得分相当低；另一方面，QDA和天真贝叶斯在特异性方面得分相对较高，但在敏感性方面却没有那么高。根据定义，高灵敏度（特异性）源于低的假阴性（阳性）率，这在数据中也有体现。
提取单个模型
## 提取随机森林模型
bmr_rf = bmr2$clone(deep = TRUE)$filter(learner_ids = 'classif.ranger.tuned')
## ROC
autoplot(bmr_rf,type = "roc")+
scale_color_discrete() +
theme_bw()
## PRC
autoplot(bmr_rf, type = "prc")+
scale_color_discrete() +
theme_bw()
ROC 
PRC
关于哪种学习器效果最好，也包括是否应该使用超量取样，在很大程度上取决于敏感性和特异性的现实意义。就实际的重要性而言，两者中的一个可能会超过另一个很多倍。想想典型的HIV快速诊断测试的例子，以低特异性为代价的高灵敏度可能会引起（不必要的）震惊，但除此之外并不危险，而低灵敏度则是非常危险的。正如通常的情况一样，这里不存在黑白分明的 "最佳模型"。回顾一下，即使有超额取样，我们的模型没有一个在灵敏度和特异性方面表现良好。在我们的案例中，我们需要思考：以低灵敏度为代价的高特异性的后果是什么，这意味着告诉许多肝病患者他们是健康的；而以低特异性为代价的高灵敏度的后果是什么，这意味着告诉许多健康患者他们有肝病。在没有进一步的特定主题信息的情况下，我们只能说明在所选择的特定性能指标上表现最好的学习器。如上所述，基于AUC的随机森林表现最好。此外，随机森林是灵敏度得分最高（FNR最低）的学习器，而朴素贝叶斯是特异性最好（FPR最低）的学习器。
然而，我们进行的分析决不是详尽的。在特征层面上，虽然我们在分析过程中几乎只关注了机器学习和统计分析方面，但也可以更深入地挖掘实际的主题（肝病），并尝试更彻底地理解变量以及潜在的相关性和互动性。这可能也意味着要再次考虑已经删除的变量。此外，可以对数据集进行特征工程和数据预处理，例如使用主成分分析。关于超参数的调整，可以考虑使用更大的超参数空间和评估数量的不同超参数。此外，调整也可以应用于那些被我们标记为基线学习者的一些学习器。最后，还有更多的分类器存在，特别是梯度提升和支持向量机可以另外应用于这项任务，并有可能产生更好的结果。
参考
（mlr3gallery: Liver Patient Classification Based on Diagnostic Measures ）(https://mlr3gallery.mlr-org.com/posts/2020-09-11-liver-patient-classification/)
