遗传算法求解TSP问题及MTATLAB代码

什么是遗传算法

  遗传算法在我的另一篇文章遗传算法原理案例及MATLAB代码里详细介绍过，这里不过多解释。

遗传算法在TSP问题中的改变

  在我的另一篇文章里，遗传算法的目的是求解一个函数的最大值。我们先得到第一代种群，然后不断交叉，变异，通过计算适应度来排序，选择相对优秀的个体为下一代。遗传算法在TSP问题的求解中思路和方法都差不多，但是仍有些计算方面的差别。

生成基因（个体）

 在TSP问题中，生成的个体即是旅行者经历的地点编号。如果随机生成的城市序号为$c_1=[1,2,3,4,5,6]$，即经历的城市顺序为$1\to 2\to 3\to 4\to 5\to 6\to 1$。而这就是随机生成的个体。

交叉

 因为经历的地点不能重复，每个地点的编号都不能重复，但是在交叉时当两串序列交叉时，可能就会出现重复。下面举个例子：如果随机生成的城市序号为$c_1=[1,2,3,4,5,6]$，即经历的城市顺序为$1\to 2\to 3\to 4\to 5\to 6\to 1$;随机生成的另一个随机生成的城市序号为$c_2=[3,5,6,1,2,4]$,即经历的城市顺序为$3\to 5\to 6\to 1\to 2\to 4\to 3$。用$c_1，c_2$作为父代进行交叉

 我们可以看到交叉后，地点序列重复了。

 为了解决上述问题，我看到了CSDN博主Reacubeth的文章中的两种方法：

 部分匹配交叉法和顺序交叉法有效地解决了交叉过程中编码重复的问题。

变异

 经典的变异方法是一段基因序列发生变化，在另一篇文章里则是随机取某个基因的某个点位，将其值更改。在这里，地点的序号肯定不能更改为任意值，因此，我将任意的两个地点编号进行替换。如下图所示：

计算适应度

 一般适应度都是按值从大到小进行排序，因此，这里的适应度计算取的是所经历路程的倒数。

%% 适配值函数     
%输入：
%个体的长度（TSP的距离）
%输出：
%个体的适应度值
function FitnV=Fitness(len)
FitnV=1./len;

MATLAB代码

clc,clear;
%%十个地点，随机生成每两个地点的距离
for i=1:10
    for m=1:10
        if m~=i
           city(i,m)=randi(10);
        else
            city(i,m)=0;
        end
    end
end

N = 20;                          % 种群上限
ger = 100;                       % 迭代次数
L = size(city,2);                % 基因长度
pc = 0.9;                        % 交叉概率
pm = 0.1;                        % 变异概率
for i=1:N
dna(i,:) =  randperm(L);             % 基因
end

x1 = zeros(N, L);                % 初始化子代基因，提速用
x2 = x1;                         % 同上
x3 = x1;                         % 同上
fi = zeros(N, 1);                % 初始化适应度，提速

for epoch = 1: ger               % 进化代数为100    
 F=cross(dna,pc);                %交叉操作
    x3 = dna;
      
 %% 变异操作
    for i = 1: N                          
        if rand < pm
            
            point1=randi(L);%随机取一个点位
            point2=randi(L);%随机取令一个点位
            while point1==point2%保证两个点位不一样
                point2=randi(L);
            end
            %交换两地点的位置
            z=x3(i,point1);%令z暂存一个点位
            x3(i,point1) = x3(i,point2) ;
            x3(i,point2) = z;
        end
    end
    dna = [dna;F; x3];               % 合并新旧基因
    len = PathLength(city,dna);
     y(epoch)=min(len);
     e=min(len);                %取每一代的最短距离
    fi=Fitness(len);              % 计算适应度，容易理解
    dna = [dna, fi];
    dna = flipud(sortrows(dna, L + 1));    % 对适应度进行排名
    while size(dna, 1) > N                 % 自然选择
        d = randi(size(dna, 1));           % 排名法
        if rand < (d - 1) / size(dna, 1)
            dna(d,:) = [];
            fi(d, :) = [];
        end
    end
    dna = dna(:, 1:L);
 
end
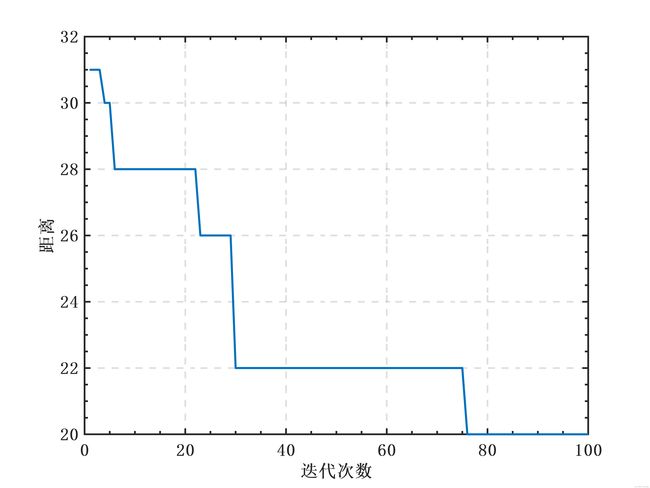
plot(y)
xlabel('迭代次数')
ylabel('距离')
disp('最短距离为')
min(y)

%% 输入种群pop，交叉概率pc
function F=cross(pop,pc)
[row,col]=size(pop);%种群的个数row(行数),城市数量col（列数）
Rang=fix(col/3);%将基因分为三段处理，这样可以使获得最优的速度更快
for i=1:row
    if rand<pc %如果满足交叉概率条件
    a1=[];
    a2=[];
    a3=[];
    b1=[];
    b2=[];
    b3=[];
%% 确定父代的两个个体
point1=randi(Rang);%确定点位1
point2=randi(Rang)+point1;%确定点位2

a1=pop(i,1:point1);%暂存第一个基因的第1段

m = randi(row); % 确定另一个交叉的个体
b1=pop(m,1:point1);%暂存第二个基因的第1段
indi(1,:)=pop(i,:);%保存两个基因以便于匹配交叉
indi(2,:)=pop(m,:);
%% 部分匹配交叉
for p=1:point1
   [x,y]=find(indi(1,:)==b1(1,p));%寻找重复的编号进行替换
   indi(x,y)=a1(1,p);
   [x,y]=find(indi(2,:)==a1(1,p));
   indi(x+1,y)=b1(1,p);
end
%% 产生两个新个体
c(i,:)=[a1,indi(2,point1+1:end)];
d(i,:)=[b1,indi(1,point1+1:end)];
    else  
%% 不满足则直接继承父代基因
c(i,:)=pop(i,:);
d(i,:)=pop(i,:);
    end  
end
F=[c;d];%得到子代基因

%% 计算各个体的路径长度
% 输入：
% D     两两城市之间的距离
% Chrom 个体的轨迹
function len=PathLength(Dist,Chrom)
[row,col]=size(Dist);
NIND=size(Chrom,1);
len=zeros(NIND,1);
for i=1:NIND
    p=[Chrom(i,:) Chrom(i,1)];
    i1=p(1:end-1);
    i2=p(2:end);
    len(i,1)=sum(Dist((i1-1)*col+i2));
end

 结果如下图所示：

 当然因为距离随机产生，每一次的运行结果都不一样。在此特别感谢CSDN博主张叔zhangshu提供的帮助，本文的部分代码也借鉴于或直接引用于张叔。