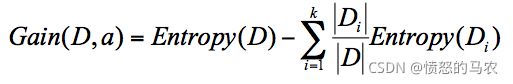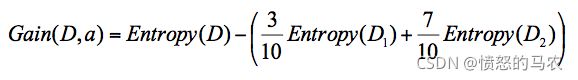机器学习实战——决策树
-
什么是决策树?介绍
决策树算法是一种归纳分类算法,它通过对训练集的学习,挖掘出有用的规则,用于对新集进行预测。
决策树算法采用树形结构,自顶向下递归方式构造决策树
决策树由下面几种元素构成:
- 根节点:包含所有的样本;
- 内部节点:对应样本特征属性;
- 分支:样本测试的结果;
- 叶子节点:代表决策的结果。
-
如何构造决策数?
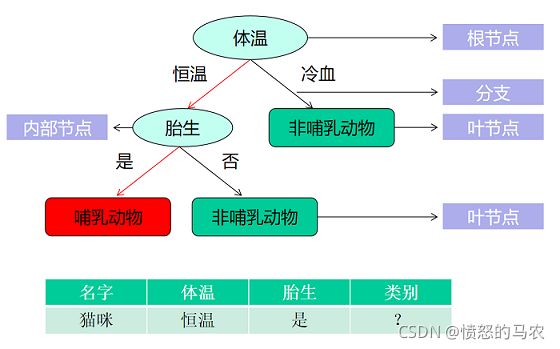
下图是关于判断猫咪是否是哺乳动物的决策树。
1.构造
什么是构造呢?构造就是生成一棵完整的决策树。简单来说, 构造的过程就是选择什么属性作为节点的过程 ,那么在构造过程中,会存在三种节点:
1)根节点:就是树的最顶端,最开始的那个节点,如上图的“体温”。
2)内部节点:就是树中间的那些节点,如上图的“胎生”;
3)叶节点:就是树最底部的节点,也就是决策结果,如上图的“哺乳动物”,“非哺乳动物”。
节点之间存在父子关系。比如根节点会有子节点,子节点会有子子节点,但是到了叶节点就停止了,叶节点不存在子节点。那么在构造过程中,你要解决三个重要的问题:
1)选择哪个属性作为根节点;
2)选择哪些属性作为子节点;
3)什么时候停止并得到目标状态,即叶节点。
例子:¶
下面我们通过一个例子对决策树的构造进行具体的讲解。 我们现在有这样一个数据集
我们该如何构造一个判断是否去打篮球的决策树呢?再回顾一下决策树的构造原理,在决策过程中有三个重要的问题:将哪个属性作为根节点?选择哪些属性作为后继节点?什么时候停止并得到目标值?
显然将哪个属性(天气、温度、湿度、刮风)作为根节点是个关键问题,在这里我们先介绍两个指标:纯度和信息熵。
先来说一下纯度。你可以把决策树的构造过程理解成为寻找纯净划分的过程。数学上,我们可以用纯度来表示,纯度换一种方式来解释就是让目标变量的分歧最小。
我在这里举个例子,假设有 3 个集合:
集合 1,6 次都去打篮球;
集合 2,4 次去打篮球,2 次不去打篮球;
集合 3,3 次去打篮球,3 次不去打篮球。
按照纯度指标来说,集合 1> 集合 2> 集合 3。因为集合 1 的分歧最小,集合 3 的分歧最大。
但是我们如何将这种分歧进行量化呢?
答案就是“信息熵”。
“信息熵”:
我们先来介绍信息熵(entropy)的概念。
1948 年, 香农 提出了“信息熵(shāng)” 的概念,解决了对信息的量化度量问题。 一条信息的信息量大小和它的不确定性有直接的关系。比如说,我们要搞清楚一件非常非常不确定的事,或是我们一无所知的事情,就需要了解大量的信息。相反,如果我们对某件事已经有了较多的了解,我们不需要太多的信息就能把它搞清楚。所以,从这个角度,我们可以认为,信息量的度量就等于不确定性的多少。
公式:
变量的不确定性越大,熵也就越大,因此我们定义的“纯度”就代表信息量的多少,我们通过信息熵就可以对各个节点进行构造了。
我举个简单的例子,假设有 2 个集合
集合 1,5 次去打篮球,1 次不去打篮球;
集合 2,3 次去打篮球,3 次不去打篮球。
在集合 1 中,有 6 次决策,其中打篮球是 5 次,不打篮球是 1 次。那么假设:类别 1 为“打篮球”,即次数为 5;类别 2 为“不打篮球”,即次数为 1。那么节点划分为类别 1 的概率是 5/6,为类别 2 的概率是 1/6,带入上述信息熵公式可以计算得出:
同样,集合 2 中,也是一共 6 次决策,其中类别 1 中“打篮球”的次数是 3,类别 2“不打篮球”的次数也是 3,那么信息熵为多少呢?我们可以计算得出:
从上面的计算结果中可以看出,信息熵越大,纯度越低。当集合中的所有样本均匀混合时,信息熵最大,纯度最低。
我们在构造决策树的时候,会基于纯度来构建。而经典的 “不纯度”的指标有三种,分别是信息增益(ID3 算法)、信息增益率(C4.5 算法)以及基尼指数(Cart 算法)。
1.ID3
ID3 算法计算的是 信息增益 ,信息增益指的就是划分可以带来纯度的提高,信息熵的下降。
在计算的过程中,我们会计算每个子节点的归一化信息熵,即按照每个子节点在跟节点中出现的概率,来计算这些子节点的信息熵。所以信息增益的公式可以表示为:
- 它的计算公式是:父节点的信息熵减去所有子节点的信息熵。
公式中 D 是根节点,Di 是子节点,Gain(D,a) 中的 a 作为 D 节点的属性选择。
假设天气 = 晴的时候,会有 5 次去打篮球,5 次不打篮球。其中 D1 刮风 = 是,有 2 次打篮球,1 次不打篮球。D2 刮风 = 否,有 3 次打篮球,4 次不打篮球。那么 a 代表节点的属性,即天气 = 晴。
针对这个例子,D 作为节点的信息增益为:
也就是 D 节点的信息熵 -2 个子节点的归一化信息熵。2 个子节点归一化信息熵 =3/10 的 D1 信息熵 +7/10 的 D2 信息熵。
我们基于 ID3 的算法规则,完整地计算下我们的训练集,训练集中一共有 7 条数据,3 个打篮球,4 个不打篮球,所以根节点的信息熵是:
如果你将天气作为属性的划分,会有三个叶子节点 D1、D2 和 D3,分别对应的是晴天、阴天和小雨。我们用 + 代表去打篮球,- 代表不去打篮球。于是我们可以用下面的方式来记录 D1,D2,D3:
D1(天气 = 晴天)={1+,2-}
D2(天气 = 阴天)={1+,1-}
D3(天气 = 小雨)={1+,1-}
我们先分别计算三个叶子节点的信息熵:
因为 D1 有 3 个记录,D2 有 2 个记录,D3 有 2 个记录,所以 D 中的记录一共是 3+2+2=7,即总数为 7。所以 D1 在 D(根节点)中的概率是 3/7,D2 在根节点的概率是 2/7,D3 在根节点的概率是 2/7。那么作为子节点的归一化信息熵 = 3/70.918+2/71.0+2/7*1.0=0.965。
因为我们用 ID3 中的信息增益来构造决策树,所以要计算每个节点的信息增益。
天气属性节点的信息增益 = 根节点信息熵 - 子节点信息熵:
Gain(D , 天气)=0.985-0.965=0.020。
同理我们可以计算出其他属性作为根节点的信息增益,它们分别为 :
Gain(D , 温度)=0.128
Gain(D , 湿度)=0.020
Gain(D , 刮风)=0.020
我们能看出来温度作为属性的信息增益最大。因为 ID3 就是要将信息增益最大的节点作为父节点,这样可以得到纯度高的决策树,所以我们将温度作为根节点。
然后我们要将第一个叶节点,也就是 D1={1-,2-,3+,4+}进一步进行分裂,往下划分,计算其不同属性(天气、湿度、刮风)作为节点的信息增益,可以得到:
Gain(D , 天气)=0
Gain(D , 湿度)=0
Gain(D , 刮风)=0.0615
我们能看到刮风为 D1 的节点都可以得到最大的信息增益,这里我们选取刮风作为节点。同理,我们可以按照上面的计算步骤得到完整的决策树。
下面我们就来构建这颗决策树!
样本数据集
还是使用上面这个例子。我们的数据集有10个样本,每个样本有各自的特征['天气','温度','湿度','刮风'],每个特征有各自的属性,比如特征“天气”有属性[“晴”,“雨”,“阴”]。
# -*- coding:utf-8 -*-
import time
import json
import math
dataset = [['晴', '高', '中', '否', '不打球'],
['晴', '高', '中', '是', '不打球'],
['阴', '高', '高', '否', '打球'],
['雨', '高', '高', '否', '打球'],
['雨', '低', '高', '否', '不打球'],
['晴', '中', '中', '是', '打球'],
['阴', '中', '高', '是', '不打球'], ]
dataLabels = ['天气', '温度', '湿度', '刮风']
class bs(object):
def __init__(self):
self.num = 0
def calcShannonEnt(self, dataSet):
"""使用math数学计算模块输出信息熵值"""
# 样本总个数,这里为个
totalNum = len(dataSet)
# 类别集合,字典数据类型
labelSet = {}
# 计算每个类别的样本个数
for dataVec in dataSet:
# 取出样本最后一列的标签'是否打球'
label = dataVec[-1] # 取最后一个
# 将label添加到labelSet集合,记录“打球”和“不打球”的数量,最后labelSet为:{'不打球': 4, '打球':3 }
if label not in labelSet.keys(): #
labelSet[label] = 0
labelSet[label] += 1 # 第一个没计入
shannonEnt = 0
# 根据学习的公式计算熵值
for key in labelSet:
pi = float(labelSet[key]) / totalNum # 打球和不打球,的数量除以总数量
shannonEnt -= pi * math.log(pi, 2) ##############
return shannonEnt
def splitDataSet(self, dataSet, feat, featvalue): # feat属性, featvalue属性值
retDataSet = []
for dataVec in dataSet:
if dataVec[feat] == featvalue:
splitData = dataVec[:feat]
splitData.extend(dataVec[feat + 1:])
retDataSet.append(splitData) # 除了feat对应的列之外,其余列都被纳入新数据集
return retDataSet
def infogain(self, dataSet, feaNum):
# 输入样本,计算样本熵值。
baseShanno = self.calcShannonEnt(dataSet)
featList = [dataVec[feaNum] for dataVec in dataSet]
# featList = []
# for dataVec in dataset:
# featList.append(dataVec[feaNum])
# print(featList)
# 找出特征属性,如'天气'的属性:“晴”,“阴”,“雨”
featList = set(featList) # 去重
newShanno = 0
# 通过熵值公式计算以第i个特征进行分类后的熵值,计算子节点熵值。如“晴”在“天气”中的熵值。
for featValue in featList:
subDataSet = self.splitDataSet(dataSet, feaNum, featValue)
prob = len(subDataSet) / float(len(dataSet))
newShanno += prob * self.calcShannonEnt(subDataSet) # 熵
infoGain = baseShanno - newShanno
return infoGain
def chooseBestFeatToSplit(self, dataSet):
# 计算总的特征个数,输出 4个
featNum = len(dataSet[0]) - 1
# 设定信息增益
maxInfoGain = 0
bestFeat = -1
# 对每一个特征进行分类,找出信息增益最大的特征
for i in range(featNum):
infoGain = self.infogain(dataSet, i)
# 找出信息增益值最大的对应特征
if infoGain > maxInfoGain:
maxInfoGain = infoGain
bestFeat = i
return bestFeat
# 创建决策树
def createDecideTree(self, dataSet, featName):
# 数据集的分类类别,“打球”,“不打球”
classList = [dataVec[-1] for dataVec in dataSet]
# 等价上面
# classList = []
# for dataVec in dataset:
# classList.append(dataVec[-1])
# 所有样本属于同一类时,停止划分,也就是说当前叶节点无法再分时,返回当前类别
if len(classList) == classList.count(classList[0]): # 判断 所有类别个数 是否等于不打球的个数
return classList[0]
# 选择最好的特征进行划分
bestFeat = self.chooseBestFeatToSplit(dataSet)
beatFestName = featName[bestFeat]
print('可建分支特征有:', beatFestName)
# 如果当前特征“bestFeat”被划分好了就将这个特征从特征集“dataLabels”中删除,不再参加计算。
del featName[bestFeat]
# 以字典形式表示决策树
DTree = {beatFestName: {}}
# 根据选择的特征,遍历该特征的所有属性值,再使用createDecideTree()函数划分叶节点。
featValue = [dataVec[bestFeat] for dataVec in dataSet]
# 将对应特征的属性按照信息增益大小排列,比如以天气特征排列,就输出{'晴', '雨', '阴'}
featValue = set(featValue)
# 将每个特征都进行以上操作,直到不能再继续分类为止。
for value in featValue:
subFeatName = featName[:]
DTree[beatFestName][value] = self.createDecideTree(self.splitDataSet(dataSet, bestFeat, value), subFeatName)
return DTree
def run(self):
myTree = self.createDecideTree(dataset, dataLabels)
print("决策树模型:")
print(myTree)
if __name__ == '__main__':
fps = bs()
fps.run()