深蓝-视觉SLAM-第一讲学习笔记
第一讲 概述与预备知识
（1）.课程内容与预备知识
（2）.SLAM是什么
（3）.视觉slam的数学表述和框架
（4）.实践：Linux下的C++编程基础
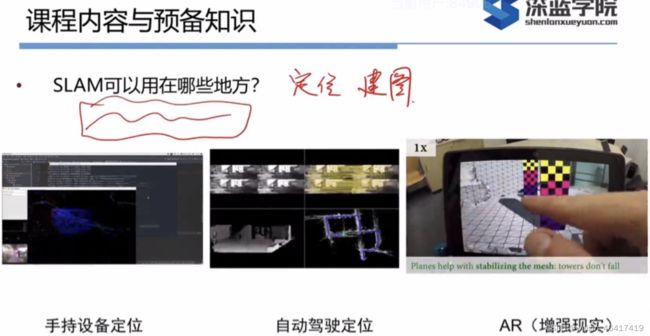
1.课程内容与预备知识
- 物体识别：指让计算机去分析或识别一张图片或者一段影片中的物体。
- 物体跟踪：找出运动的物体在每帧图像中的位置，即运动的物体在环境中是如何运动的。
- 物体检测：给指定观测图中的指定物体一个外边的框，即使用矩形框来识别图片中的对象，还包括 3D物体的外包框。
- 语义分割：将类别与图片中的每个像素关联的算法，用于区分图片中那些对象是同一类别的。
这些都是计算机视觉的任务，处理计算机视觉任务的主流方式就是训练一些神经网络，给定足够的数据，训练一些特殊结果的网络，帮助我们去解决这些事情。
给定一段视频，估计相机的运动和周围环境的状态——slam 主要关注的问题
什么是slam的定位和建图？
定位：相机或机器人在运动的过程中观测到地图中的特征点法或直接法来定位自身的位置（位姿）
建图：通过相机或机器人获取的周围环境的2D图片信息来恢复三维信息。
特征点法：特征点法所建的地图是稀疏的导致无法对周围环境物体的结构进行估计，无法实现导航避障
直接法：
高博DSO介绍：https://zhuanlan.zhihu.com/p/29177540
RGB-D相机观测到的图：深度相机，有深度信息，点云信息
-
课程内容
-
SLAM: SImultaneous Localization and Mapping .（同时定位与地图构建）:指搭载特定传感器的主体，在没有环境先验信息的情况下，与运动过程中建立环境模型，同时估计自身运动，如果传感器为相机，就称为**“视觉slam"**。
-
同时定位与地图构建
-
SLAM的数学基础知识
-
SLAM相关的计算机视觉知识
-
工程实践
2.SLAM是什么？
定位和建图是相互耦合，相互依赖的问题（当前运动物体的位置是与全局的环境进行比较后确定的，全局的地图结构是依赖与当前运动物体的位置构建的）
slam依赖传感器进行定位（内置传感器）和建图（外置传感器）
传感器分为两类：
-
携带与机器人本体上的——同常测量的是间接的物理量而不是直接的位置数据，只能通过一些间接的手段来推算自己的位置，这种定位方案适合与未知的环境。
-
安装与环境中的——通常能直接测量机器人的位置信息，有效的解决定位问题，但由于受到环境的约束，当约束无法满足时，就无法进行定位，它无法提供一个普遍的，通用的解决方案。
相机采集到的图像是3D信息在相机成像平面上的投影（成相的过程中丢失掉了深度信息），图片连续采集就形成了视频（20HZ， 30HZ）每秒采集到的图像的帧数（20-30张）
单目相机：无法通过单张图片来计算场景中的物体与相机的距离，如果想恢复三维结构，必须改变相机的视角（场景中物体的大小和远近称为结构 近处的物体移动快，远处的物体运动慢，极远处的物体看上去是不动的，通过移动相机，形成视差来判断物体的远近。）。单目slam估计的轨迹和地图与真实的轨迹和地图相差一个因子（尺度），单目slam无法仅凭图像来确定这个尺度——尺度不确定性。单目slam平移之后才能计算深度。
双目相机：通过某种手段可以测量物体离相机的距离，克服了单目相机无法知道距离的缺点。双目相机由两个单目相机组成，这两个相机之间的距离——基线，通过基线可以确定每个像素的空间位置（基线越大，能测量到的物体就越远）。双目相机或多目相机的缺点是配置和标定比较复杂，深度量程和精度受双目的基线和分辨率的限制，视差的计算量耗时，需要使用GPU和FPGA加速，才能输出整张图片的距离信息，计算量是双目的问题之一。
深度相机（RGB-D）：可以通过红外结构光和ToF（Time-of-Flight)原理，主动向物体发射光并接受返回光，测得舞体到相机的距离，通过这种物理手段可以节省大量的计算资源（RGB-D相机包括Kinect/Kinect V2, Xtion Pro Live, RealSense等）。深度相机的缺点：测量范围窄，噪声大，视野小，易受日光干扰，无法测量投射材料，主要用于室内。
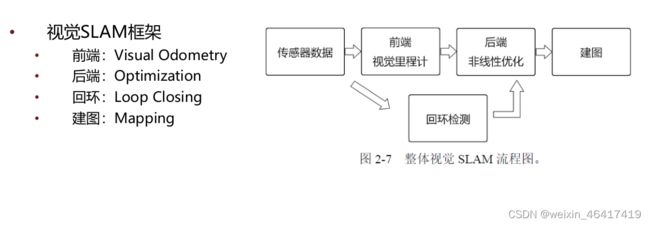
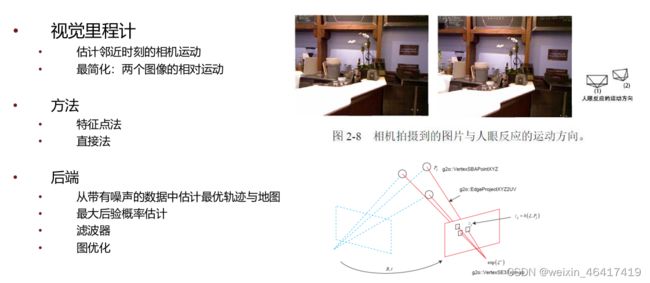
视觉里程计： 关心相邻图像间的相机运动，如何根据图像来确定相机的运动，就需要知道相机与空间点的几何关系。（相邻时刻的运动串联构成了机器人的运动轨迹，解决了定位问题，根据每个时刻的相机位置，计算出了像素的空间点位置，得到了地图？）
- 视觉里程计只估计了两个图像间的运动，而每次的估计都有一定的误差，由于里程计的工作方式，导致先前时刻的误差会传递到下一时刻，一段时间后，估计的轨迹不准确——累积漂移
- 如何解决漂移问题？——>后端优化和回环检测：回环检测负责检测机器人是否回到原点，后端优化根据该信息，校正整个轨迹的形状。
后端：如何从这些带有噪声的数据中估计整个系统的状态，以及这个状态（机器人的轨迹和地图）的不确定性大小（最大后验概率估计）
回环检测： 解决位置估计随时间漂移问题，解决方法实际上是一种计算机图像数据相似性算法，通过回环检测，将A，B是同一点的信息传到后端，后端的优化算法会根据这一信息将地图调整到符合回环检测结果的样子，如果我门有正确且充分的回环检测，就可以消除累积误差，得到全局一致的轨迹和地图。
地图： 分为度量地图和拓扑地图
-
度量地图：强调精确表示地图中的物体位置关系，分为稀疏（Sparse)和稠密(Dense)。稀疏地图是由一部分具有代表意义的路标点组成的，稀疏地图适合定位，稠密地图适合导航（导航算法：A* ， D*）。
-
拓扑地图：拓扑地图更关注地图中个元素之间的关系。
3.视觉SLAM的数学描述
相机是在某些时刻采集的数据，将连续时间的运动离散化了，所以我们也之关系这些时刻的位置和地图。于是各时刻的位置记作x1, x2,…xk,每个时刻传感器会测量到一些路标，记作y1,y2,y3…yN。如何用数学语言来描述相机的运动和观测呐？
Uk:运动传感器的读数或者输入 Wk:该过程中加入的噪声 Vk,j:这次观测的噪声
运动方程的参数化形式：Uk,输入的指令是两个时刻间的位置和转角变化量Δx1, Δx2, θ
激光传感器观测一2D路标点时，能够测量到距离和夹角，记路标点为yj = [ y 1 , y 2 ] T \mathbf{[y1,y2]}^\mathrm{T } [y1,y2]Tj 位姿为Xk = [ x 1 , x 2 ] T \mathbf{[x1,x2]}^\mathrm{T } [x1,x2]Tk, 观测数据为Zk,j = [ r ， ϕ ] T \mathbf{[r，ϕ]}^\mathrm{T } [r，ϕ]T，观测方程如下：
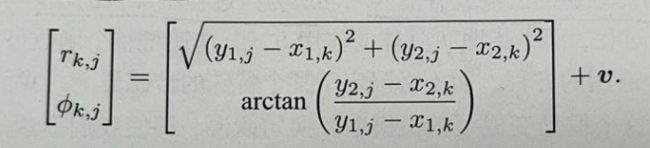观测方程就是对路标点进行拍摄后，得到图像中像素的过程，这个与相机模型有关。
状态估计问题的求解，与两个方程的具体形式有关，以及噪声服从哪种分布有关。按照运动和观测方程是否为线性，噪声是否服从高斯分布，将系统分为线性/非线性/和高斯/非高斯系统。其中线性高斯（Linear Gaussian ,LG)最简单，它的无偏的最优估计由卡尔曼滤波（Kalman Filter,KF)给出。 而非线性非高斯（Non-Linear Non-Gaussian,NLNG),使用扩展卡尔曼滤波（EKF）和非线性优化来求解，EKF，即在工作点处将其线性化，并以预测–更新两不步骤来求解。