Human-level control through deep reinforcement learning

Human-level control through deep reinforcement learning

文章出处:Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540):529.
文章连接: 链接
文章标题加*的不是原作者标题，是根据个人理解加上的

Abstract*

  强化学习理论关于agents如何优化对它们对环境的控制, 提供了一个规范的解释，强化学习理论深深植根于动物行为的心理和神经科学的角度中。然而，为了在接近现实世界复杂性的情况下成功地使用强化学习，agents面临着一个困难的任务：他们必须从高维的感知输入中获得对环境的有效表示，并利用这些信息将过去的经验推广到新的情境中。值得注意的是，人类和其他动物似乎通过强化学习和分级感官处理系统harmonious (和谐的) 结合来解决这个问题，前者被大量的神经数据所证实，这些数据揭示了多巴胺能神经元产生的相位信号与时间差分强化学习(TD)算法之间的显著并行得到验证。虽然强化学习agents已经在许多领域取得了一些成功，但之前它们的适用性仅限于：手工设计的有用特征的领域，或完全观察到的低维状态空间的领域。在这里(Here)，我们利用训练深层神经网络的最新进展开发一种新的智能体agent，称为deep Q-network agent，它可以通过端到端强化学习直接从高维感知输入中学习成功的策略。我们在经典的Atari2600游戏中测试了这个agent。实验证明，deep Q-network agent只接收像素和游戏分数作为输入，能够在49个游戏集中超越所有先前算法的性能，达到与专业人类游戏测试人员相当的水平，使用相同的算法、网络架构和超参数。这项工作弥合了高维感官输入和动作之间的鸿沟 (bridges…between桥接。此处翻译成弥合…鸿沟) ，从而产生了第一个能够学会在各种挑战性任务中表现出色的智能agent。

Introduce

  我们设计去创建了一个单一的算法，它能够广泛的处理各种挑战性任务—一般的人工智能，无法达到这个效果。为了实现这一目标，我们开发了一种新的agent，a deep Q-network(DQN)，它能够将强化学习与人工神经网络(称为深层神经网络)相结合。值得注意的是(notably)，最近深层神经网络的进展，使用了几层节点来逐步建立更抽象的数据表示，使得人工神经网络能够直接从原始感官数据中学习诸如对象分类之类的概念。我们使用了一种特别成功的架构，即深卷积网络，它使用分层的层叠卷积滤波器来模拟感受野的影响，这种效应是由Hubel和Wiesel在早期视觉皮层的前馈处理方面的开创性工作所启发的，从而利用图像中的局部空间相关性，以及增强对自然变化的鲁棒性，如视角或尺度的变化。
  我们考虑的任务中，agents通过一系列的observations，actions and rewards, 考虑agent和环境交互的任务。该agent的目标是:为了得到最大的积累reward，而选择actions。正式的(More formally), 我们使用一个深层卷积神经网络来近似最优动作值-函数(the optimal action-value function):$$Q^{\ast }(s,a)=\underset{\pi }{\max }\mathbb{E}[r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+...|s_t=s,a_t=a,\pi ],$$这是在进行观察(s)和采取行动(a)之后,由行为策略$\pi =P(a|s)$实现每个时间步骤$t$,最大回报综合$r_t$,其中$\gamma$是衰减因子。
   强化学习著名的问题是:当用一个非线性函数估计，如：一个神经网络来表示动作-值函数时，就会导致不稳定或者不收敛。这个不稳定主要有几个原因导致的：序列观察的相关性(the correlations present in the sequence of observations), 对Q值的小更新可能会显著的改变策略，从而改变数据分布，以及动作-值(Q)和目标值之间的关系。我们利用新颖的Q-Learning的变体来解决这些不稳定问题，主要用到了两个ideas：

1. 我们使用了一种生物学启发机制, 被称为经验回放(experience replay), 对数据进行随机化处理，从而消除观察序列中的相关性，使得在数据分布上平滑变化（详见下文）。
2. 我们使用了一个迭代更新来调整动作-值(Q)，使之朝向只定期更新的目标值(target values)，从而减少与目标的联系。

   虽然在强化学习环境中还有其他稳定的训练神经网络算法，如：netral fitted Q-iteration, 这些方法涉及到网络重复训练，需要上百次迭代。因此，与我们的算法不同，这些方法效率太低，无法成功地用于大型神经网络。我们使用图1所示地深度卷积网络参数化近似值函数$Q(s,a;{\delta }_i)$,其中${\delta }_i$是第i次迭代的Q-network的参数。为了实现经验重现(experience replay),我们在数据集$D_t=\{e_1,...,e_t\}$中存储每个时间步t agent的经验$e_t=(s_t,a_t,r_t,s_{t+1})$。在学习的过程中，我们对从存储样本中随机抽取的经验样本$(s,a,r,s^{\prime })\sim U(D),$应用Q-learning更新，第i次迭代的Q-learning更新损失函数如下：$$L_i({\theta }_i)={\mathbb{E}}_{s,a,r,s^{\prime }\sim U(D)}[(r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime };{\theta }_i^{-})-Q(s,a;{\theta }_i){)}^2]$$ 其中，$\gamma$是折扣因子，决定了agent的视野。

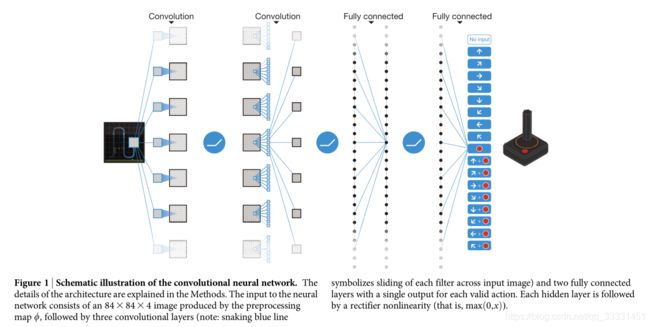
fig1.卷积神经网络示意图。方法中对体系结构的细节进行了说明。神经网络的输入由预处理图$\varphi$生成的84x84x4图像组成，然后是三个卷积层（注：蛇形蓝线表示每个filter（卷积核）在输入图像上滑动）和两个完全连接的层，每个有效操作有一个单独的输出。每个hide layer(隐含层)后面都有一个整流器非线性（即$\max (0,x)$）。

   为了评估我们的DQN代理，我们利用了Atari 2600平台，该平台提供了各种各样的任务(n=49), 这些任务都是为人类玩家设计的。我们使用相同的网络架构、超参数值（见扩展数据表1）和学习过程，以高维数据（60赫兹, 210x160彩色视频）为输入，为了证明我们的方法能够在各种游戏中稳健地学习成功的策略，这些策略完全基于感官输入，并且只有非常少的先验知识（也就是说，仅仅输入数据是视觉图像，以及每个游戏中可用的动作数，而不是它们的对应关系；参见方法）。值得注意的是，我们的方法能够以稳定的方式使用强化学习信号和随机梯度下降来训练大型神经网络——如两个学习指标的时间演化所示（代理的每集平均得分和平均预测Q值；详见图2和补充讨论）。值得注意的是，我们的方法能够以稳定的方式使用强化学习信号和随机梯度下降来训练大型神经网络——如两个学习指标的时间演化所示（agent的每片段平均得分和平均预测Q值；详见图2和补充讨论）。

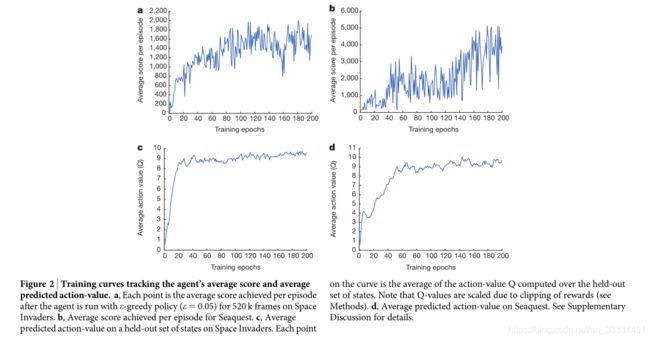
fig2.训练曲线跟踪agent的平均得分和平均预测动作值。a, 每一点是agent在 Space
Invaders(一种游戏)上使用$ϵ-greedy$策略（$ϵ=0.05$）运行520k帧后每episode获得的平均分数。b,Seaquest(可能是一种游戏)每episode平均得分 c,对Space Invaders一组状态的平均预测action-value。曲线上的每个点都是在保持状态集上计算的作用值Q的平均值。请注意，Q值是根据奖励的削减而定的（见Method）。d, 在Seaquest上的平均预测动作值。详见补充讨论。

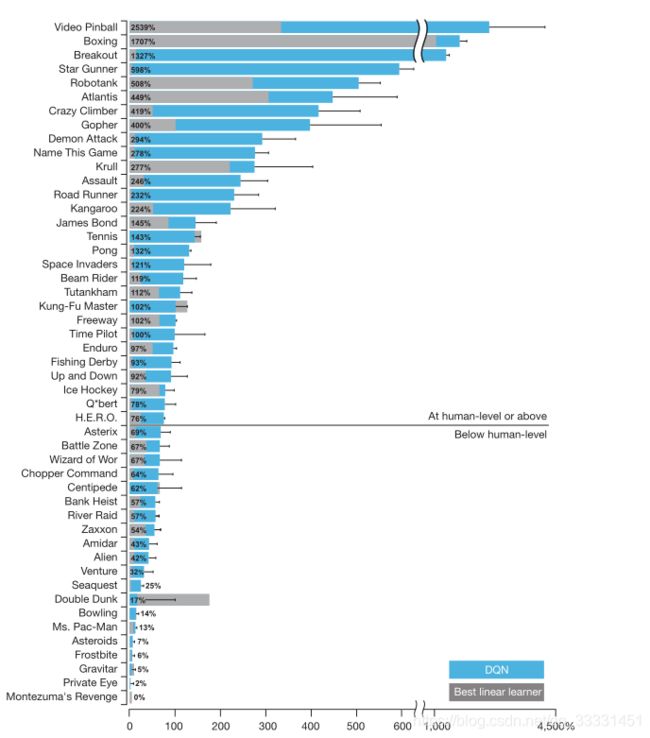
  我们将DQN与强化学习文献中的最佳执行方法进行了比较，在49个游戏中，结果是有效的。除了学习的agent外，我们还报告了在受控条件下玩的专业人体游戏测试人员的分数，以及随机统一选择动作的策略（扩展数据表2和图3，在y轴上用100%（人类）和0%（随机）表示；见Methods）。我们的DQN方法在43个游戏中优于现有的最佳强化学习方法，而不包含其他方法使用的关于Atari 2600游戏的任何额外先验知识。此外，我们的DQN代理在49场比赛中的表现与专业人体游戏测试人员相当，在超过一半的游戏（29场游戏；参见图3，补充讨论和扩展数据表2）.在附加仿真中（见补充讨论和扩展数据表3和4），我们通过禁用DQN agent的各个核心组件（the replay memory、独立目标Q网络和深度卷积网络体系结构）并演示其对性能的不利影响，从而证明了它们的重要性。

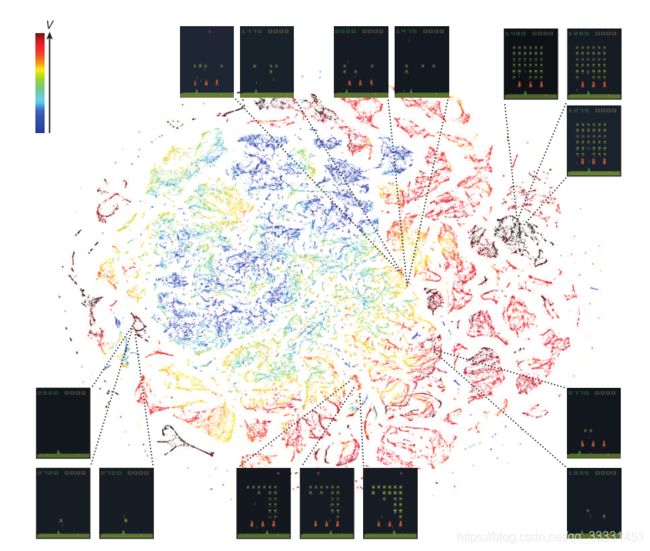
  接下来，我们研究了DQN所学的表示法，这些表示法通过使用一种称为“t-SNE”25（图4）的高维数据可视化技术，在游戏空间入侵者的背景下支撑了anget的成功性能（参见补充视频1）。正如预期的那样，t-SNE算法倾向于将感知相似状态的DQN表示映射到附近的点。有趣的是，我们还发现t-SNE算法为DQN状态表示生成了类似的嵌入，这些状态在期望回报方面很接近，但是感知上的不同（图4，右下、左上和中），与网络能够从高维感官输入中学习支持适应性行为的表示的概念相一致。此外，我们还证明了DQN学习到的表示能够泛化为从策略生成的数据，而不是在模拟中，我们将其作为输入呈现给人类和anget玩游戏时所经历的网络游戏状态，记录最后一个隐藏层的表示，并可视化了t-SNE算法生成的嵌入（扩展数据图1和补充讨论）。扩展数据图2提供了由DQN学习的表示如何允许其准确地预测状态和动作值的附加说明。
  值得注意的是，DQN擅长的游戏在性质上有着极大的差异，从侧翻射击（River Raid）到拳击游戏（Boxing）和三维赛车游戏（Enduro）。事实上，在某些游戏中，DQN能够发现一个相对长期的策略（例如，突破：anget学习最佳策略，即首先在墙的一侧挖一个隧道，让球绕着墙的背面发送，从而摧毁大量的积木；关于DQN在训练过程中的表现发展，请参见补充视频2）。尽管如此，对于包括DQN在内的所有现有anget来说，需要更多时间扩展的计划策略的游戏仍然是一个重大的挑战（例如Montezuma的复仇）。


  在这项工作中，我们证明了一个单一的体系结构可以在一系列不同的环境中成功地学习控制策略，只接收像素和游戏分数作为输入，并且在每个游戏中使用相同的算法、网络结构和超参数，只知道人类玩家的输入。与之前的研究不同，我们的方法采用了“端到端”强化学习，该学习使用奖励在卷积网络中不断地塑造表征，使其朝向有利于价值估计的环境的显著特征。这一原理利用了神经生物学的证据，即知觉学习中的奖赏信号可能会影响灵长类动物视觉皮层的表征特征。值得注意的是，强化学习与深层网络体系结构的成功集成，关键在于我们采用了一种回放算法，该算法涉及最近经历的转换的存储和表示。越来越多的证据表明，海马体可能支持哺乳动物大脑中这种过程的物理实现，在离线期间，最近经历的轨迹经过时间压缩重新激活（例如，提供一种假定的机制，通过与基底神经节的相互作用可以有效地更新价值函数。在未来，探索将经验重演的内容偏向于显著事件的潜在用途是很重要的，这种现象是经验性观察到的海马重放的特征，并与强化学习中的“优先扫除”概念有关。综上所述，我们的工作说明了利用最先进的机器学习技术和受生物启发的机制来创建能够学习掌握各种挑战性任务的代理的力量。

Method

参考：https://zhuanlan.zhihu.com/p/35245722