深蓝-视觉slam-第六讲学习笔记
上一讲中,使用了特征点估计了相机的运动,本讲的光流法和直接法不需要特征匹配好的点就可以估计相机的位姿。
特征点法来估计相机运动的缺点:
- 关键点的提取和描述子的计算非常耗时。SIFT在CPU上无法实时计算,ORB也需要花费20毫秒的时间,如果整个SLAM以30毫秒/帧的速度运行,一半时间花在了计算描述子上;
- 使用特征点时,忽略了除特征点之外的所有信息。一幅图像有几十万个像素,而特征点有几百个,只用特征点会丢失大部分有用的信息。
- 相机会运动到特征点缺失的地方,这些地方没有明显的纹理。使得我们找不到足够的匹配点来估计相机运动。
克服特征点缺点的方法:
- 保留特征点,但只计算关键点,不计算描述子。同时,使用光流法(Optical Flow)跟踪特征点的运动。这样可以回避计算和匹配描述子带来的时间,而光流本身的计算时间要小于描述子的计算和匹配时间。
- 只计算关键点,不计算描述子。同时使用直接法(Direct Method)计算特征点在下一时刻图像中的位置。这样可以跳过计算描述子的时间,也省去了计算光流的时间。
使用光流法克服计算和匹配描述子的方法,仍然使用特征点,只是匹配描述子替换成了光流跟踪,估计相机运动时,仍使用对极几何,PnP,ICP算法。这依然要求提取到的关键点具有可区别性,即我们需要提取角点。 而在直接法中,我们根据像素灰度信息同时估计相机运动和点的投影,不需要提取到点必须是角点。他们甚至可以是随机算取得点。
使用特征点法估计相机的运动时,我们把特征点看作固定在三维空间中的不动点。根据他们在相机中的投影位置,通过最小化重投影误差(Reprojection error)来优化相机的运动。在这个过程中我们需要知道空间点到两个相机中投影后的像素位置————这也就是要对特征点进行匹配和追踪的原因。同时,使用特征点法时计算和匹配特征需要付出很大的计算量。
在直接法中,我们不需要知道点与点(此时的点不一定是角点)的对应关系,通过最小化光度误差来估计相机的运动。
光流法:通过灰度不变假设,找出不同时刻下同一点的在不同图像中的匹配,对应关系。然后可以通过ICP,PnP,ICP等方法计算相机运动。这样一种两步走的方案,很难保证全局的最优性。

直接法是为了克服特征点法的缺点而提出的。直接法根据像素的亮度信息估计相机的运动,可以完全不用计算关键点和描述子,避免了特征的计算时间和特征点的缺失情况。只要场景中存在明暗变化(可以是渐变,不形成局部的图像梯度),直接法就能工作。
根据使用的像素的数量,直接法分为:稠密,稀疏,半稠密.与特征点法只能重构稀疏特征点(稀疏地图)相比,直接法具有恢复稠密,半稠密结构的功能。

直接法是从光流演变而来,光流描述了像素在图像中的运动,直接法则附带着一个相机的运动模型。
光流是一种描述像素随时间在图像之间运动的方法。

灰度不变假设:同一个空间点的像素灰度值,在各个图像中是固定不变的。



如果相机运动过快,两张图像差别较明显,那么单层光流法容易达到一个局部极小值。此时可以引入图像金字塔来改善。
图像金子塔是指对同一个图像进行缩放,得到不同分辨率下的图像,以原始图像作为金子塔底层,每往上一层,就对下层图像进行一定倍率的缩放,就得到一个金子塔,然后,在计算光流时,先从顶层的图像开始计算,然后把上一曾的追踪结果作为下一层的初始值。由于上一层的相对粗糙,这个过程也是由粗到精的光流。

光流法可以加速基于特征点的视觉里程计算法,避免计算和匹配描述子的过程,但要求相机运动较平滑(或采集频率较高)。



在特征点法中,由于通过匹配描述子知道了P1,p2两像素的位置,所以可以计算重投影误差的位置。
但在直接法中,由于没有特征匹配,我们就无法知道p1,p2的对应关系。直接法的思路就是根据当前相机的位姿估计(粗略的估计)寻找p2的位置,若相机的位姿不够好,p2的外观和p1的会有明显差别。为了减小这个差别,需要优化相机的位姿,来寻找与p1更相近的p2.

直接法的优化变量是相机的位姿T,而不像光流那样优化各个特征点的运动。e是如何随着相机的位姿变化的

上式利用了李代数的左扰动模型,利用一阶泰勒展开。


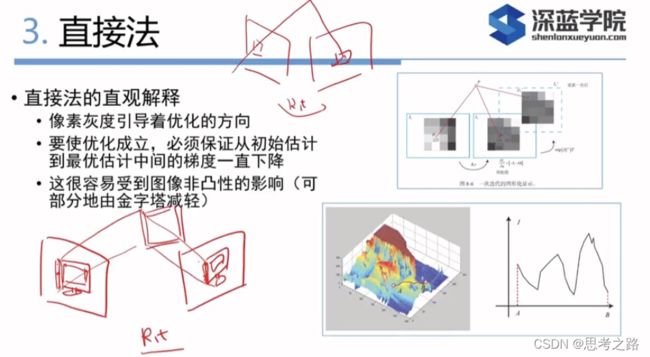
相比与特征点法,直接法完全依靠优化来求解相机的位姿,而像素梯度引导这优化的方向,如果我们想要正确的优化结果,就必须保证大部分像素梯度能把优化引导到正确的方向.
参考图像一个灰度值为299, 假设我们给的相机位姿的初值比较差,这个初值下,空间点P投影后的像素灰度值是126,像素误差是299-126,为了减少这个误差,我们需要微调相机的位姿,使像素更亮一些. 相机位姿微调的方向是需要用到像素梯度。在微调的过程中,我们用像素的局部梯度近似了它附近的灰度分布,不过真实图像并不是光滑的,所以这个梯度在远处就不成立了。
但是优化算法不能只凭单个像素,需要考虑很多个像素后,优化算法才能原则一个方向,计算出一个更新量 δ T \delta T δT。加上这个更新量后,投影后的像素移动到了一个更量的地方。通过这次更新,使得误差变小,多次迭代,最后收敛
直接法的梯度是直接由图像梯度确定的,因此我们必须保证沿着梯度走时,灰度误差会不断下降,然而,由于图像通常是一个很强烈的非凸函数,实际中,我们沿着图像梯度前进,很容易由于图像本身的非凸函数性(或噪声)落入一个局部极小值中,无法继续优化。只有当相机运动很小,图像中的梯度不会有很强的非凸性时,直接法才成立.

实践
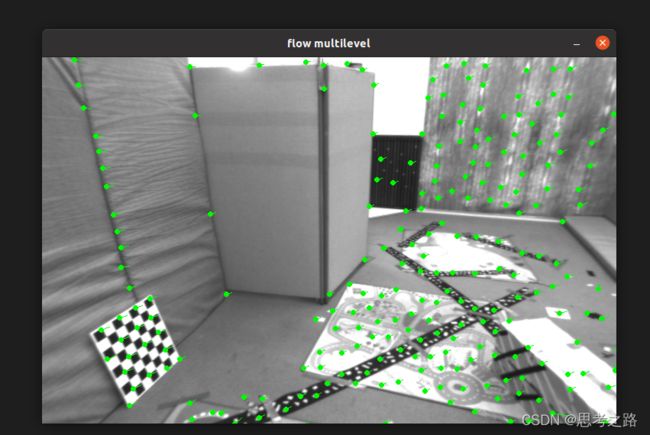
1.使用OpenCV自带的cv::calcOpticalFlowPyrLK函数来追踪上面的特征点,提供两张图像和对应的特征点,即可得到追踪后的点,以及各点的状态,误差,可以根据status变量是否为1,来确定对应的点是否被追踪到。
#include 实现效果:

2,高斯牛顿法实现单层光流和多层光流
单层光流:
光流也可以被看作优化问题:通过最小化灰度误差估计最优的像素偏移。
在OpticalFlowSingleLevel函数中实现了单层光流函数,其中调用了cv::parallel_for并行调用了OpticalFlowTracker::calculateOpticalFlow,该函数计算了指定范围内特征点的光流。这个并行for循环内部是Intel tbb库实现的,只需要根据接口,将函数体定义出来,然后将函数作为std::function对象传递给它。
在函数体calculateOpticalFlow()解决如下问题:
min △ x , △ y \min\limits_{\triangle_x, \triangle_y} △x,△ymin ∥ I 1 ( x , y ) − I 2 ( x + △ x , y + △ y ) ∥ 2 2 \lVert I_1(x,y) - I_2(x + \triangle x, y + \triangle y) \rVert^2_2 ∥I1(x,y)−I2(x+△x,y+△y)∥22
残差是括号里的部分,对应的J是第二个图像在 x + △ x x + \triangle x x+△x, y + △ y y + \triangle y y+△y处的梯度。这里的梯度可以用第一个图的梯度来代替 I 1 ( x , y ) I_1(x,y) I1(x,y), 这种代替方式:反向光流法。在反向光流法中,这个梯度是不变的,所以我们可以在第一次时保留计算的结果,在后续迭代中使用。J不变,H不变,每次迭代只算残差。
#include #include pt1, pt2;
// for(auto &kp: keypoint1s)
// pt1.push_back(kp.pt);
// vector status;
// vector error;
// t1 = chrono::steady_clock::now();
// calcOpticalFlowPyrLK(image1, image2, pt1, pt2, status, error);
// t2 = chrono::steady_clock::now();
// auto time_used = chrono::duration_cast>(t2 - t1);
// cout << "optical flow by opencv:" << time_used.count() << endl;
//单层光流
// vector key2_single;
// vector status_single;
// t1 = chrono::steady_clock::now();
// opticalFlowSingleLevel(image1, image2, keypoint1s, key2_single, status_single);
// t2 = chrono::steady_clock::now();
// auto time_used = chrono::duration_cast>(t2 - t1);
// cout << "optical flow by single:" << time_used.count() << endl;
//多层光流
vector<KeyPoint> keypoint2_multi;
vector<bool> status_multi;
t1 = chrono::steady_clock::now();
OpticalFlowMultiLevel(image1, image2, keypoint1s, keypoint2_multi, status_multi, true);
t2 = chrono::steady_clock::now();
auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "optical flow by multi:" << time_used.count() << endl;
// Mat image2_CV;
// cvtColor(image2, image2_CV, CV_GRAY2BGR); //将原视图转换为灰度图
// for(int i = 0; i < pt2.size(); i++) {
// if(status[i]) {
// circle(image2_CV, pt2[i], 2, Scalar(0,250, 0), 2);
// line(image2_CV, pt1[i], pt2[i], Scalar(0, 250, 0));
// }
// }
// Mat image2_single;
// cvtColor(image2, image2_single, CV_GRAY2BGR);
// for(int i = 0; i < key2_single.size(); i++) {
// if(status_single[i]) {
// circle(image2_single, key2_single[i].pt, 2, Scalar(0, 250, 0), 2);
// line(image2_single, keypoint1s[i].pt, key2_single[i].pt, Scalar(0, 250, 0));
// }
// }
Mat image2_multi;
cvtColor(image2, image2_multi, CV_GRAY2BGR);
for(int i = 0; i < keypoint2_multi.size(); i++) {
if(status_multi[i]){
circle(image2_multi, keypoint2_multi[i].pt, 2, Scalar(0, 250, 0), 2);
line(image2_multi, keypoint1s[i].pt, keypoint2_multi[i].pt, Scalar(0, 250, 0));
}
}
imshow("原图", image1);
// imshow("opencv flow", image2_CV);
// imshow("flow single", image2_single);
imshow("flow multilevel" , image2_multi);
waitKey(0);
while(char(waitKey(1)) != 'q') {}
return 0;
}
void opticalFlowSingleLevel(const Mat &image1, const Mat &image2, const vector<KeyPoint> &keypoint1s, vector<KeyPoint> &keypoint2_single, vector<bool> &status_single, bool inverse, bool has_initial)
{
keypoint2_single.resize(keypoint1s.size());
status_single.resize(keypoint1s.size());
OpticalFlowTracker tracker(image1, image2, keypoint1s,keypoint2_single, status_single, inverse, has_initial);
parallel_for_(Range(0, keypoint1s.size()), std::bind(&OpticalFlowTracker::calculateOpticalFlow, &tracker, placeholders::_1));
}
void OpticalFlowTracker::calculateOpticalFlow(const Range &range)
{
int half_patch_size = 4;
int iterations = 10;
for(size_t i = range.start; i < range.end; i++) {
auto kp = kp1[i];
double dx = 0 , dy = 0;
if(has_initial) {
dx = kp2[i].pt.x - kp.pt.x;
dy = kp2[i].pt.y - kp.pt.y;
}
double cost = 0, lastCost = 0;
bool succ = true;
//高斯牛顿迭代
Eigen::Matrix2d H = Eigen::Matrix2d::Zero();
Eigen::Vector2d b = Eigen::Vector2d::Zero();
Eigen::Vector2d J;
for(int iter = 0; iter < iterations; iter++) {
if(inverse == false) {
H = Eigen::Matrix2d::Zero();
b = Eigen::Vector2d::Zero();
} else {
b = Eigen::Vector2d::Zero();
}
cost = 0;
//计算cost和J
for(int x = -half_patch_size; x < half_patch_size; x++)
for(int y = -half_patch_size; y < half_patch_size; y++) {
double error = GetPixelValue(image1, kp.pt.x + x, kp.pt.y + y) -
GetPixelValue(image2, kp.pt.x + x + dx, kp.pt.y + y + dy);
if (inverse == false) {
J = -1.0 * Eigen::Vector2d(
0.5 * ( GetPixelValue(image2, kp.pt.x + dx + x + 1, kp.pt.y + dy + y) -
GetPixelValue(image2, kp.pt.x + dx + x - 1, kp.pt.y + dy + y)),
0.5 * (GetPixelValue(image2, kp.pt.x + dx + x, kp.pt.y + dy + y + 1)-
GetPixelValue(image2, kp.pt.x + dx + x, kp.pt.y + dy + y -1))
);
} else if(iter == 0) {
J = -1.0 * Eigen::Vector2d(
0.5 * (GetPixelValue(image1, kp.pt.x + x + 1, kp.pt.y + y) -
GetPixelValue(image1, kp.pt.x + x - 1, kp.pt.y + y)),
0.5 * (GetPixelValue(image1, kp.pt.x + x, kp.pt.y + y + 1) -
GetPixelValue(image1, kp.pt.x + x, kp.pt.y + y - 1))
);
}
b += -error * J;
cost += error * error;
if(inverse == false || iter == 0) {
H += J * J.transpose();
}
}
Eigen::Vector2d update = H.ldlt().solve(b);
if(std::isnan(update[0])) {
cout << "update is nan" << endl;
succ = false;
break;
}
if(iter > 0 && cost > lastCost) {
break;
}
dx += update[0];
dy += update[1];
lastCost = cost;
succ = true;
if(update.norm() < 1e-2) {
break;
}
}
success[i] = succ;
kp2[i].pt = kp.pt + Point2f(dx,dy);
}
}
void OpticalFlowMultiLevel(const Mat &image1, const Mat &image2, const vector<KeyPoint> &keypoint1s, vector<KeyPoint> &keypoint2_multi, vector<bool> &status_multi, bool inverse)
{
int pyramids = 4;
double pyramid_scale = 0.5;
double scales[] = {1.0, 0.5, 0.25, 0.125};
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
vector<Mat> pyr1, pyr2;
for(int i = 0; i<pyramids; i++) {
if(i == 0)
{
pyr1.push_back(image1);
pyr2.push_back(image2);
} else {
Mat img1_pyr, img2_pyr;
cv::resize(pyr1[i-1], img1_pyr, cv::Size(pyr1[i-1].cols * pyramid_scale, pyr1[i-1].rows * pyramid_scale));
cv::resize(pyr2[i-1], img2_pyr, cv::Size(pyr2[i-1].cols * pyramid_scale, pyr2[i-1].rows * pyramid_scale));
pyr1.push_back(img1_pyr);
pyr2.push_back(img2_pyr);
}
}
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "build pyramid time: " << time_used.count() << endl;
//由粗到精在层上追踪
vector<KeyPoint> kp1_pyr, kp2_pyr;
for(auto &kp:keypoint1s) {
auto kp_top = kp;
kp_top.pt *= scales[pyramids - 1];
kp1_pyr.push_back(kp_top);
kp2_pyr.push_back(kp_top);
}
for(int level = pyramids-1; level >= 0; level--)
{
status_multi.clear();
t1 = chrono::steady_clock::now();
opticalFlowSingleLevel(pyr1[level], pyr2[level], kp1_pyr, kp2_pyr, status_multi, inverse, true);
t2 = chrono::steady_clock::now();
auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "track pyr"<< level << "cost time:" << time_used.count() << endl;
if(level > 0){
for(auto &kp: kp1_pyr)
kp.pt /= pyramid_scale;
for(auto &kp: kp2_pyr)
kp.pt /= pyramid_scale;
}
}
for(auto &kp:kp2_pyr)
keypoint2_multi.push_back(kp);
}
cmake_minimum_required(VERSION 2.8)
project(ch8)
set(CMAKE_BUILD_TYPE "Release")
add_definitions("-DENABLE_SSE")
set(CMAKE_CXX_FLAGS "-std=c++11 ${SSE_FLAGS} -g -O3 -march=native")
find_package(OpenCV 3 REQUIRED)
include_directories( ${OpenCV_INCLUDE_DIRS} "/usr/include/eigen3/")
add_executable(optical_flow optical_flow.cpp)
target_link_libraries(optical_flow ${OpenCV_LIBS})

LK光流跟踪能够直接得到特征点的对应关系.这个对应关系就像描述子匹配,只是光流对图像的连续性和光照稳定性要求高一些.我们通过光流来跟踪特征点,用PnP,ICP或对极几何来估计相机运动.
总结: 光流法可以加速基于特征点的视觉里程计算法,避免计算和匹配描述子的过程,单要求相机运动较平滑(或采用频率较高).
单层直接法:
实现代码:
#include 运行结果:






多层光流:
left_png 分别与5张图片进行光度误差计算R,t,每一对有四层金字塔的追踪。
当金字塔对图像进行缩放时,对应的内参也要乘以相同的倍率。
首先,我们读取第一个图像left.png,在对应的视差图disparity.png中,计算每个像素对应的深度,然后对000001.png~000005.png这五张图像,利用直接计算相机的位姿。为了展现直接法的对特征点不敏感性,我们随机的在第一张图像中选取一些点,不使用任何角点或特征点提取算法。
实现代码:
#include 运行结果:
如下图片是000001.png图片的四层金字塔的追踪结果, 还有同样的4组(000002,000003,000004,000005.png)这样的多层直接法的追踪结果;(键盘ctrl键实现)



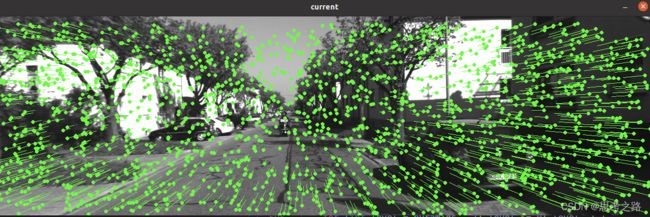
000001.png四层追踪的结果:

000002.png四层追踪的结果:
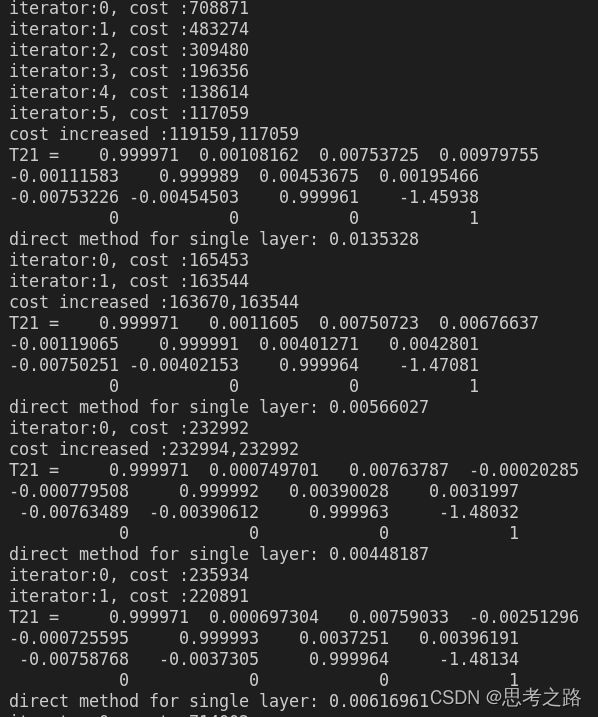
000003.png四层追踪的结果:

000004.png四层追踪的结果:

000005.png四层追踪的结果: