【Apollo 6.0算法解析】Apollo EM Planner

---

前言

EM Planner是基于轻决策的规划算法。与其他基于重决策的算法相比，EM Planner的优势在于能够处理许多复杂的场景（例如多障碍物的场景）。当基于重决策的方法试图预先确定如何处理每个障碍物时，困难是显而易见的：（1）很难理解和预测障碍物如何与主车相互作用，因此它们的跟随运动难以描述，因此很难被任何规则考虑；（2）当多个障碍物阻塞道路时，无法找到满足所有预定决策的轨迹概率大大降低，从而导致规划的失败。

Planning的大概流程是这样：先由 Routing模块通过全局规划得到参考线 Reference Line，然后 Planning模块在此基础上进行局部轨迹规划，EM Planner将路径和速度进行分层规划，并在 SL 和 ST坐标系下，使用动态规划（DP）进行路径和速度的决策和粗规划，然后再使用二次规划（QP）进行平滑处理。

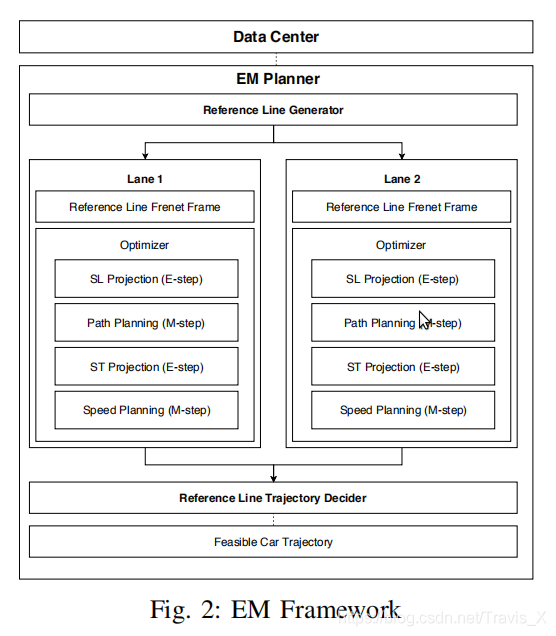
在第一个E-steps中，动态和静态障碍物都被投影到Frenet框架。静态障碍物会直接从笛卡尔坐标系转换到Frenet坐标系，而动态障碍物的信息则以其运动轨迹来描述。在Apollo框架中，可以预测动态障碍物的移动轨迹。考虑到之前的周期规划轨迹，我们可以在每个时间点估计出动态障碍物和汽车的位置。然后动态障碍物和汽车在某个时间点的重叠可以被映射到Frenet框架中。另外，动态障碍物的出现会最终导致自车做出避让的决策。因此，出于安全考虑，SL投影只考虑低速和来向障碍物，而对于高速的动态障碍物，EM Planner的平行变道策略会考虑这种情景。

在第二个E-steps中，基于生成的路径在s-t坐标系下，所有障碍物包括高速、低速和即将到来的障碍物都将被估计,生成速度曲线。如果障碍物轨迹和已经规划的路径重叠，将在s-t坐标系下对应区域将会在进行重新生成。

在两个M-steps中，通过动态规划和二次规划生成路径和速度曲线。尽管我们将障碍物投影到SL和ST坐标系下，但是最优的路径和速度解仍在非凸空间中。因此，我们使用动态规划先获得一个粗略解，同时，这个解可以提供避让、减速、超车等障碍决策。通过这个粗略的解，可以构建一个凸包，然后使用基于二次规划的样条优化器来求解。

---

一、SL 和 ST 坐标系

1.1 SL坐标系

SL坐标系又称为Frenet坐标系，S代表中心线方向，L代表与中心线正交的方向，在SL坐标系中，我们用S、L、侧向速度dL、侧向加速度ddL、侧向加加速度dddL，这5个量描述车辆的状态。

在Frenet坐标系下做运动规划的好处在于借助于指引线做运动分解，将高维度的规划问题，转换成了多个低维度的规划问题，极大的降低了规划的难度。另外一个好处在于方便理解场景，无论道路在地图坐标系下的形状与否，我们都能够很好的理解道路上物体的运动关系。相较直接使用地图坐标系下的坐标做分析，使用Frenet坐标，能够直观的体现道路上不同物体的运动关系。

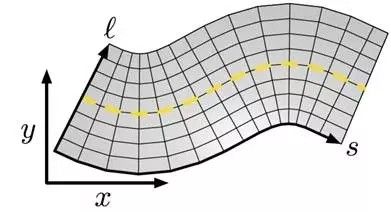
1.2 ST坐标系

ST坐标系可以帮助我们设计和选择速度曲线，“S”表示车辆的纵向位移，“T”表示时间，ST图上的曲线是对车辆运动的描述，因为它说明了车辆在不同时间的位置，由于速度是位置变化的速率，因此可以通过曲线的斜率从ST图上推断速度，斜坡越陡说明在短时间内有更大的移动对应更快的速度。

---

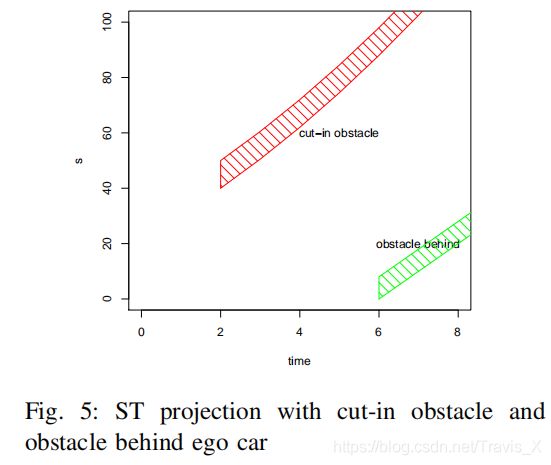
二、DP Path（E-Step）

基于动态规划的路径步骤提供一条粗略的路径信息，其可以带来可行通道和避障决策。这一步包括Lattice采样、目标代价函数、动态规划搜索。过程如下所示：

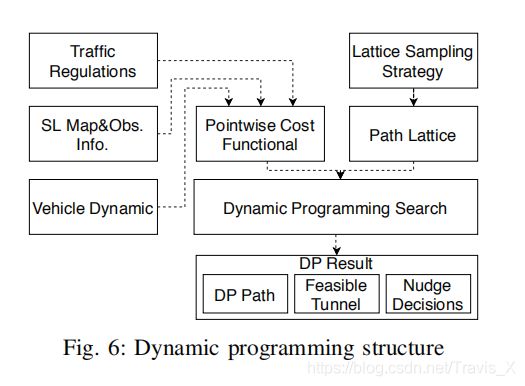
2.1 Lattice采样

Lattice采样是基于Frenet坐标的。如7图所示，首先在车辆之前对多行lattice进行采样。不同行之间的点通过五次多项式来平滑连接。行之间的间隔距离取决于速度，道路结构，变换车道等。出于安全考虑，路径总长可以达到200m或者覆盖8s的行驶长度。


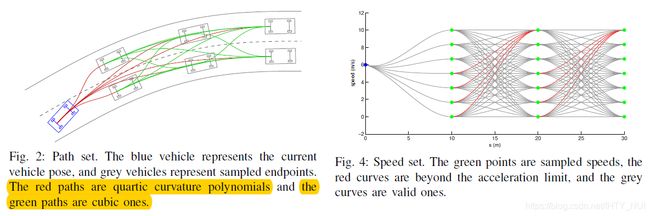
2.2 代价函数

每段Lattice路径的代价通过光滑程度、障碍物代价、车道代价来评价：

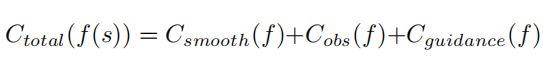
2.2.1 光滑程度

光滑程度通过以下方程来衡量，一阶导表示朝向偏差，二阶导表示曲率，三阶导表示曲率导数：

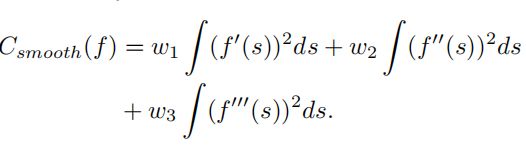
2.2.2 障碍物的代价

障碍物的代价通过以下方程来衡量，“d”代表的是车辆bounding box到障碍物bounding box的距离。
$C_{nudge}$定义为单调递减函数，出于安全方面的考虑，$d_c$设置保留缓冲区，可根据情况微调$d_n$范围。$C_{collision}$是碰撞代价函数，可帮助检测不可行的路径。

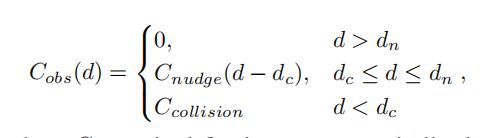
2.2.3 车道代价

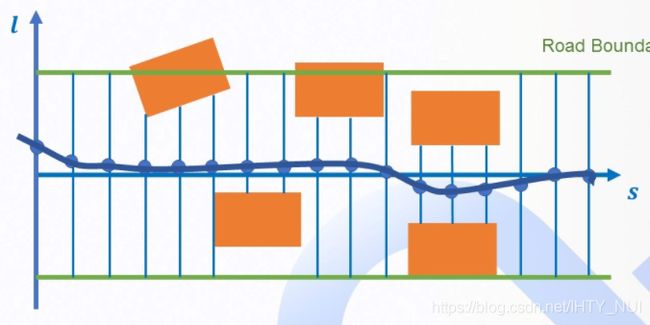
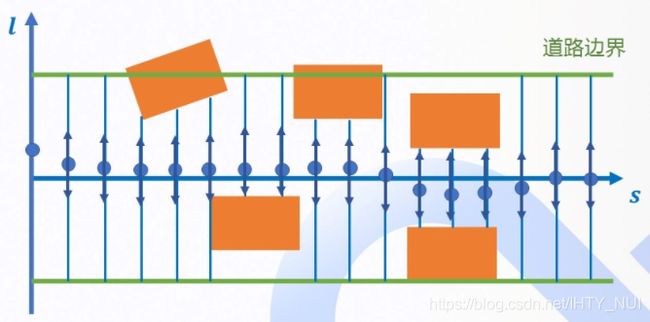
车道代价通过以下方程来衡量，主要是考虑在车辆行驶路线与车道中心线的差异。车道代价函数包括两个部分：引导线代价和车道代价。引导线定义为周围没有障碍物时的理想路径，通常这条线提取的是道路中心线。车道代价函数通常被道路边界决定，在道路外的路径点会受到很高代价的惩罚：

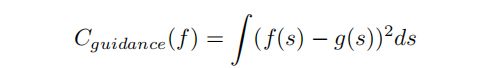
3.1 动态规划

DP路径算法的基本思路是，基于给定的一条中心路径（称为参考线，Reference Line）和车道边界条件，每隔一定间隔的纵向距离（称为不同级（level）上的S值）对道路截面进行均匀采样（与中心点的横向偏移值称为为L值），这样会得到图中黑点所示的采样点（这些采样点称为航点，waypoint）数组。基于一定的规则，可以给出各航点迁移的代价值（cost）。航点迁移不一定需要逐级进行，可以从第一级跳到第三级甚至终点，只要迁移代价值最小化即可，这显然满足动态规划的求解思路。

---

三、Spline Path（M-Step）

DP path（E-Step）这一步已经可以求解出一条粗略的可行路径，而样条QP要做的就是平滑这个DP输出来的路径。

QP求解器求解具有线性约束的目标函数生成最优的QP路径，过程如下：

3.1 代价函数

QP路径的代价函数是平滑度代价和引导线代价的线性组合。该步骤中的引导线是动态规划挑选出来的路径。引导线提供了避开障碍物的估计值。在数学上QP路径步骤优化以下函数：

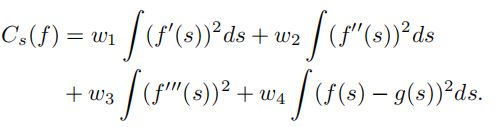
$g(s)$是动态规划的结果。$f^{\prime }(s)$、${}^{\prime \prime }(s)$,、$f^{\prime \prime \prime }(s)$分别为航向角、曲率和曲率的变化率。该目标函数描述了避开障碍物和平滑度之间的权衡。

3.2 约束条件

DP的约束有两个：boundary constraints（边界约束） 和 dynamic feasibility（动力学约束）。

3.2.1 boundary constraints

边界约束也可以理解为碰撞约束，可以在车头车尾加两个半圆作为车辆边界以保证约束的线性和凸性。

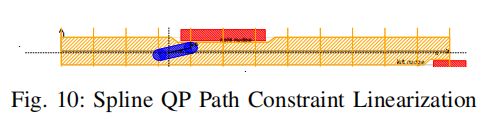
然后左前角的横向位置由以下表示，其中θ是汽车和道路状态方向之间的航向角。

可用下面的不等式进一步近似地线性约束：

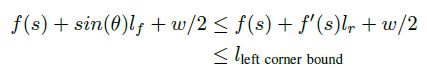
3.2.2 dynamic feasibility

DP给出了由很多points（每个row上一个point）组成guidance line，QP可以此为基础调整每个point在L方向的位置以实现平滑path。但调整是有可行范围的，该范围可量化为QP的约束（lmin和lmax）。另外曲率$f^{\prime \prime }(s)$和曲率变化率$f^{\prime \prime \prime }(s)$也可以用dynamic feasibility去约束衡量（如下图）。

---

四、DP Speed Optimizer（E-Step）

DP速度算法的基本思路是，在DP路径算法生成一条可行驶的路径后，从起点开始，考虑避开路径中的所有障碍物，并且让加减速最为平顺，以最优的速度曲线（即t-s平面中的绿色曲线）安全抵达终点，这也可以使用动态规划的思路求解。

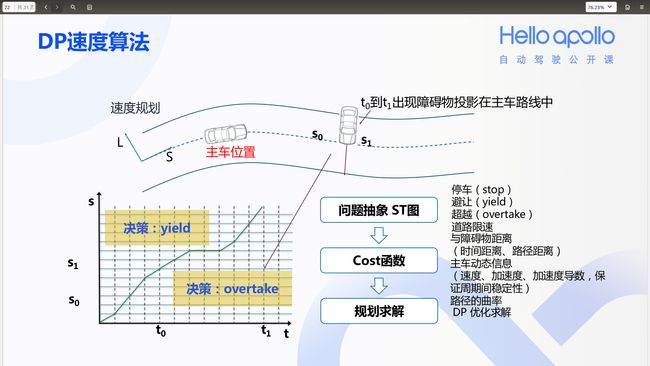
DP速度规划步骤包括ST图网格、代价函数和动态规划搜索，分别生成分段性速度曲线，可行的走廊和障碍物速度决策。

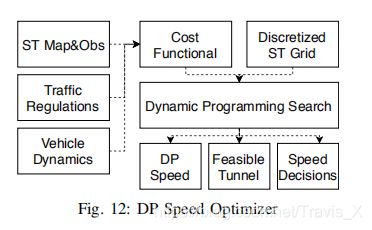
4.1 ST图

障碍物信息首先在ST图上离散成网格。将$（t_0,t_1\dots t_n)$表示为在时间轴上具有间隔$d_t$的等距评估点。分段性速度曲线函数在网格上表示为$S=（s_0,s_1,\dots s_n）$。此外，利用有限差分方法对导数进行了逼近。

4.2 代价函数

目标是在ST图中优化一个带有约束的代价函数。准确地说，DP速度优化器的代价表示为：

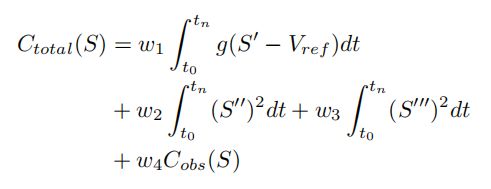
• 速度保持代价：表示当没有障碍物或者没有红绿灯时，车辆应按照指定的速度行驶。${}_{ref}$ 描述的是参考速度，参考速度由道路速度限制、曲率和其他交通规则来确定，g函数被用来对小于或者大于$V_{ref}$值施加的不同惩罚。
• 加速度a和加加速度jerk描述了速度曲线的平滑代价；
• $C_{obs}$值描述了总障碍代价，对车辆到所有的障碍物的距离进行评估，确定总障碍物代价。

4.3 动态规划搜索

动态规划搜索空间必须在动力学约束范围内。动态约束包括加速度、加加速度jerk和单调性约束。因为要求生成的轨迹在道路上不执行倒车的操作，只能在泊车或者其他指定情况下直行倒车。搜索算法是向前的，基于车辆动态约束的一些必要修剪也被应用以加速该过程。

---

五、Spline QP Speed Optimizer（M-Step）

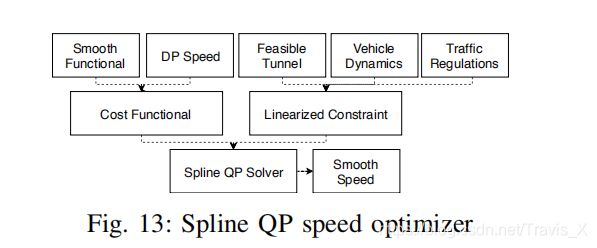
由于分段线性速度曲线不能满足动力学要求，需要用QP来解决这个问题。在图13中，样条速度包括三个部分：代价函数、线性约束条件。

5.1 代价函数

代价函数可以这样表示：

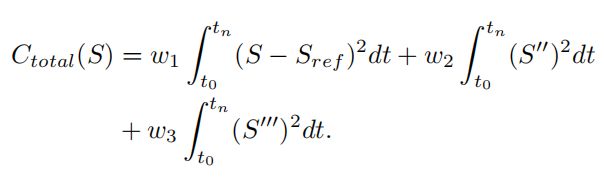
第一项是DP得出的速度曲线和最后QP生成的速度曲线之间的距离。第二、三项是平滑衡量，加速度和jerk。因此，目标函数是为了平衡引导线和平滑度。

5.2 约束

QP优化器是带有线性约束的。QP速度优化器的线性约束如下，其中：
第1项是单调性：保证车辆只能前行不能倒车；
第2项是ST曲线在某一时刻的上下界，算是表征碰撞的约束；
第3项是车速上限，一般从交通规则或车辆动力学得出；
第4项是加速度限制，一般由车辆动力学性能、舒适性决定；
第5项是加加速度限制，一般也由车辆动力学性能、舒适性决定；

---

参考

Apollo Lattice Planner从学习到放弃.额不…到实践
[论文解读]Baidu Apollo EM Motion Planner
动态规划及其在Apollo项目Planning模块的应用
自动驾驶之轨迹规划6——Apollo EM Motion Planner

---