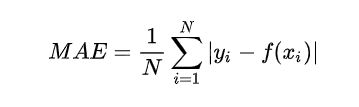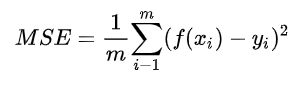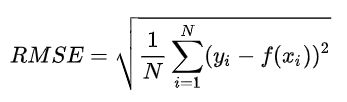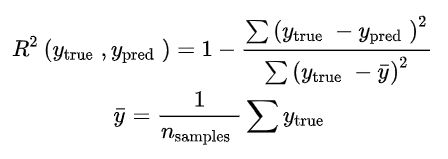Python二手车价格预测(二)—— 模型训练及可视化
系列文章目录
一、Python数据分析-二手车数据获取用于机器学习二手车价格预测
二、Python二手车价格预测(一)—— 数据处理
文章目录
- 系列文章目录
- 前言
- 一、明确任务
- 二、模型训练
-
- 1.引入库
- 2.读入数据
- 3.评价指标
- 4.线性回归
- 5.K近邻
- 6.决策树回归
- 7.随机森林
- 8.XGBoost
- 9.集成模型Voting
- 10.Tensorflow神经网络
- 11.各模型结果
- 三、重要特征筛选
- 结语
前言
前面分享了二手车数据获取的内容,又对获取的原始数据进行了数据处理,相关博文可以访问上面链接。许多朋友私信我问会不会出模型,今天模型baseline来了!允许我抛砖引玉,有什么地方描述的不恰当或者有问题,请各位朋友们评论指正!
一、明确任务
一般的预测任务分为回归任务和分类任务,二手车的价格是一个连续值,因此二手车价格预测是一个回归任务。
回归任务的模型有很多,如:线性回归、K近邻(KNN)、岭回归、多层感知机、决策树回归、极限树回归、随机森林、梯度提升树……
诸多模型中有一部分模型是通过多个弱学习器集成起来的模型,像随机森林、Voting等,它们具有更强的学习能力,集成多个单一学习器得到最终结果,一般集成模型的预测效果表现都很良好。
为了给大家提供一个二手车价格预测的baseline,我将选取几个经典模型进行训练。
二、模型训练
1.引入库
代码如下:
# 写在前面,大家可以关注一下微信公众号:吉吉的机器学习乐园
# 可以通过后台获取数据,不定期分享Python,Java、机器学习等相关内容
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
import sys
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
pd.set_option('display.max_rows', 100,'display.max_columns', 1000,"display.max_colwidth",1000,'display.width',1000)
from sklearn.metrics import *
from sklearn.linear_model import *
from sklearn.neighbors import *
from sklearn.svm import *
from sklearn.neural_network import *
from sklearn.tree import *
from sklearn.ensemble import *
from xgboost import *
import lightgbm as lgb
import tensorflow as tf
from tensorflow.keras import layers
from sklearn.preprocessing import *
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import *
2.读入数据
代码如下:
# final_data.xlsx 是上一次分享最后数据处理后的
data = pd.read_excel("final_data.xlsx", na_values=np.nan
# 将数据划分输入和结果集
X = data[ data.columns[1:] ]
y_reg = data[ data.columns[0] ]
# 切分训练集和测试集, random_state是切分数据集的随机种子,要想复现本文的结果,随机种子应该一致
x_train, x_test, y_train, y_test = train_test_split(X, y_reg, test_size=0.3, random_state=42)
3.评价指标
- 平均绝对误差(MAE)
平均绝对误差的英文全称为 Mean Absolute Error,也称之为 L1 范数损失。是通过计算预测值和真实值之间的距离的绝对值的均值,来衡量预测值与真实值之间的距离。计算公式如下:
- 均方误差(MSE)
均方误差英文全称为 Mean Squared Error,也称之为 L2 范数损失。通过计算真实值与预测值的差值的平方和的均值来衡量距离。计算公式如下:
- 均方根误差(RMSE)
均方根误差的英文全称为 Root Mean Squared Error,代表的是预测值与真实值差值的样本标准差。计算公式如下:
- 决定系数(R2)
决定系数评估的是预测模型相对于基准模型(真实值的平均值作为预测值)的好坏程度。计算公式如下:
-
最好的模型预测的 R2 的值为 1,表示预测值与真实值之间是没有偏差的;
-
但是最差的模型,得到的 R2 的值并不是 0,而是会得到负值;
-
当模型的 R2 值为负值,表示模型预测结果比基准模型(均值模型)表现要差;
-
当模型的 R2 值大于 0,表示模型的预测结果比使用均值预测得到的结果要好。
定义评价指标函数:
# 评价指标函数定义,其中R2的指标可以由模型自身得出,后面的score即为R2
def evaluation(model):
ypred = model.predict(x_test)
mae = mean_absolute_error(y_test, ypred)
mse = mean_squared_error(y_test, ypred)
rmse = sqrt(mse)
print("MAE: %.2f" % mae)
print("MSE: %.2f" % mse)
print("RMSE: %.2f" % rmse)
return ypred
4.线性回归
代码如下:
model_LR = LinearRegression()
model_LR.fit(x_train, y_train)
print("params: ", model_LR.get_params())
print("train score: ", model_LR.score(x_train, y_train))
print("test score: ", model_LR.score(x_test, y_test))
predict_y = evaluation(model_LR)
输出结果:
params: {'copy_X': True, 'fit_intercept': True, 'n_jobs': None, 'normalize': False}
train score: 0.823587700962806
test score: 0.7654427047191524
MAE: 1.97
MSE: 25.90
RMSE: 5.09
我们可以将 y_test 转换为 numpy 的 array 形式,方便后面的绘图。
test_y = np.array(y_test)
由于数据量较多,我们取预测结果和真实结果的前50个数据进行绘图。
plt.figure(figsize=(10,10))
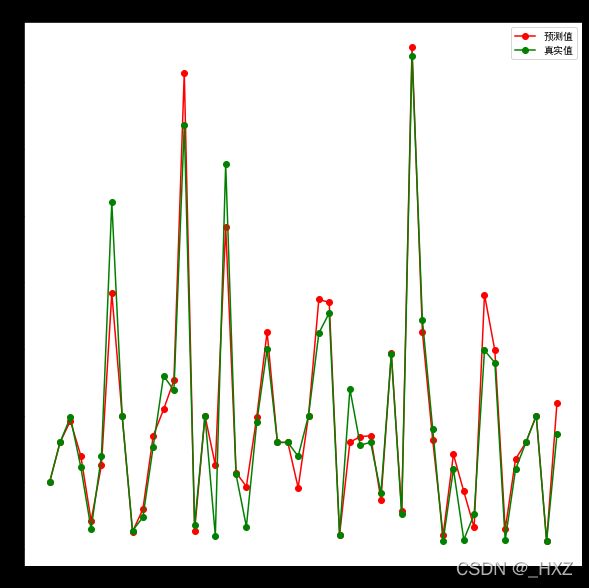
plt.title('线性回归-真实值预测值对比')
plt.plot(predict_y[:50], 'ro-', label='预测值')
plt.plot(test_y[:50], 'go-', label='真实值')
plt.legend()
plt.show()

上图中,绿色点为真实值,红色点为预测值,当两点几乎重合时,说明模型的预测结果十分接近。
5.K近邻
代码如下:
model_knn = KNeighborsRegressor()
model_knn.fit(x_train, y_train)
print("params: ", model_knn.get_params())
print("train score: ", model_knn.score(x_train, y_train))
print("test score: ", model_knn.score(x_test, y_test))
predict_y = evaluation(model_knn)
输出结果:
params: {'algorithm': 'auto', 'leaf_size': 30, 'metric': 'minkowski', 'metric_params': None, 'n_jobs': None, 'n_neighbors': 5, 'p': 2, 'weights': 'uniform'}
train score: 0.8701966571367806
test score: 0.7886892618747352
MAE: 1.35
MSE: 23.33
RMSE: 4.83
绘图:
plt.figure(figsize=(10,10))
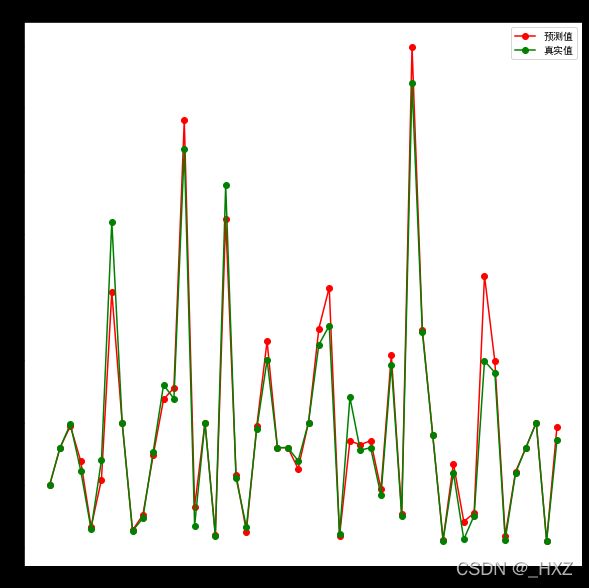
plt.title('KNN-真实值预测值对比')
plt.plot(predict_y[:50], 'ro-', label='预测值')
plt.plot(test_y[:50], 'go-', label='真实值')
plt.legend()
plt.show()
6.决策树回归
代码如下:
model_dtr = DecisionTreeRegressor(max_depth = 5, random_state=30)
model_dtr.fit(x_train, y_train)
print("params: ", model_dtr.get_params())
print("train score: ", model_dtr.score(x_train, y_train))
print("test score: ", model_dtr.score(x_test, y_test))
predict_y = evaluation(model_dtr)
在这里,决策树学习器加入了一个 max_depth 的参数,这个参数限定了树的最大深度,设置这个参数的主要原因是为了防止模型过拟合
输出结果:
params: {'criterion': 'mse', 'max_depth': 5, 'max_features': None, 'max_leaf_nodes': None, 'min_impurity_decrease': 0.0, 'min_impurity_split': None, 'min_samples_leaf': 1, 'min_samples_split': 2, 'min_weight_fraction_leaf': 0.0, 'presort': False, 'random_state': 30, 'splitter': 'best'}
train score: 0.8339532311129941
test score: 0.7857733129009127
MAE: 2.16
MSE: 18.37
RMSE: 4.29
如果不限定树的最大深度会发生什么呢?
model_dtr = DecisionTreeRegressor(random_state=30)
model_dtr.fit(x_train, y_train)
print("params: ", model_dtr.get_params())
print("train score: ", model_dtr.score(x_train, y_train))
print("test score: ", model_dtr.score(x_test, y_test))
predict_y = evaluation(model_dtr)
输出结果:
params: {'criterion': 'mse', 'max_depth': None, 'max_features': None, 'max_leaf_nodes': None, 'min_impurity_decrease': 0.0, 'min_impurity_split': None, 'min_samples_leaf': 1, 'min_samples_split': 2, 'min_weight_fraction_leaf': 0.0, 'presort': False, 'random_state': 30, 'splitter': 'best'}
train score: 0.999999225529954
test score: 0.8673942873037808
MAE: 1.16
MSE: 14.64
RMSE: 3.83
获得树的最大深度:
model_dtr.get_depth()
输出结果:
38
我们发现,在不限定树的最大深度时,决策树模型的训练得分(R2)为:0.999999225529954,但测试得分仅为:0.8673942873037808。
这就是模型过拟合,在训练数据上的表现非常良好,当用未训练过的测试数据进行预测时,模型的泛化能力不足,导致测试结果不理想。
感兴趣的同学可以自行查阅关于决策树剪枝的过程。
绘图:
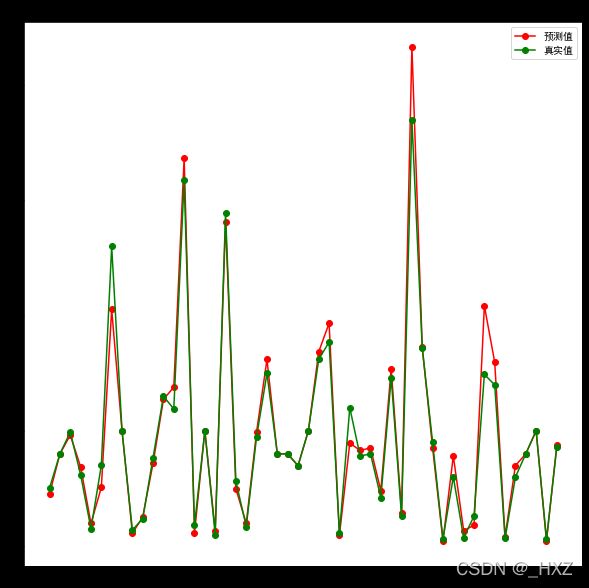
plt.figure(figsize=(10,10))
plt.title('决策树回归-真实值预测值对比')
plt.plot(predict_y[:50], 'ro-', label='预测值')
plt.plot(test_y[:50], 'go-', label='真实值')
plt.legend()
plt.show()
7.随机森林
代码如下:
model_rfr = RandomForestRegressor(random_state=30)
model_rfr.fit(x_train, y_train)
print("params: ", model_rfr.get_params())
print("train score: ", model_rfr.score(x_train, y_train))
print("test score: ", model_rfr.score(x_test, y_test))
predict_y = evaluation(model_rfr)
输出结果:
params: {'bootstrap': True, 'criterion': 'mse', 'max_depth': None, 'max_features': 'auto', 'max_leaf_nodes': None, 'min_impurity_decrease': 0.0, 'min_impurity_split': None, 'min_samples_leaf': 1, 'min_samples_split': 2, 'min_weight_fraction_leaf': 0.0, 'n_estimators': 10, 'n_jobs': None, 'oob_score': False, 'random_state': 30, 'verbose': 0, 'warm_start': False}
train score: 0.9873589573962257
test score: 0.9004628017201377
MAE: 0.88
MSE: 10.99
RMSE: 3.32
绘图:
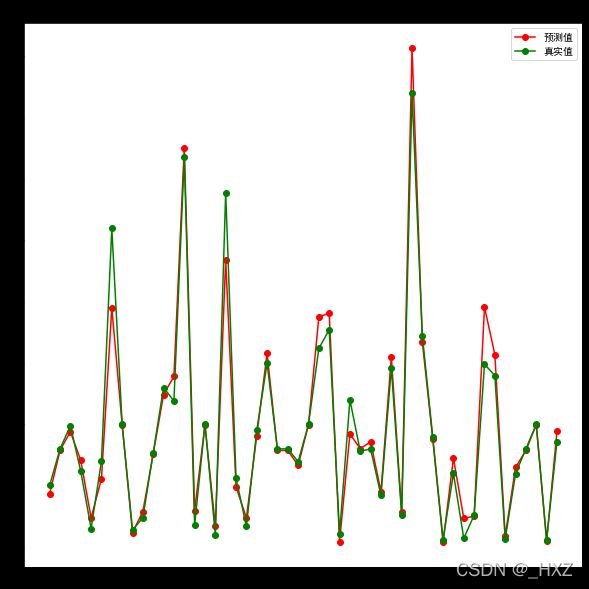
plt.figure(figsize=(10,10))
plt.title('随机森林-真实值预测值对比')
plt.plot(predict_y[:50], 'ro-', label='预测值')
plt.plot(test_y[:50], 'go-', label='真实值')
plt.legend()
plt.show()
8.XGBoost
XGboost是华盛顿大学博士陈天奇创造的一个梯度提升(Gradient Boosting)的开源框架。至今可以算是各种数据比赛中的大杀器,被大家广泛地运用。
代码如下:
model_xgbr = XGBRegressor(n_estimators = 200, max_depth=5, random_state=1024)
model_xgbr.fit(x_train, y_train)
print("params: ", model_xgbr.get_params())
print("train score: ", model_xgbr.score(x_train, y_train))
print("test score: ", model_xgbr.score(x_test, y_test))
predict_y = evaluation(model_xgbr)
输出结果:
params: {'objective': 'reg:squarederror', 'base_score': 0.5, 'booster': 'gbtree', 'colsample_bylevel': 1, 'colsample_bynode': 1, 'colsample_bytree': 1, 'gamma': 0, 'gpu_id': -1, 'importance_type': 'gain', 'interaction_constraints': '', 'learning_rate': 0.300000012, 'max_delta_step': 0, 'max_depth': 5, 'min_child_weight': 1, 'missing': nan, 'monotone_constraints': '()', 'n_estimators': 200, 'n_jobs': 0, 'num_parallel_tree': 1, 'random_state': 1024, 'reg_alpha': 0, 'reg_lambda': 1, 'scale_pos_weight': 1, 'subsample': 1, 'tree_method': 'exact', 'validate_parameters': 1, 'verbosity': None}
train score: 0.9897272945187993
test score: 0.8923618501911923
MAE: 0.88
MSE: 11.88
RMSE: 3.45
绘图:
plt.figure(figsize=(10,10))
plt.title('XGBR-真实值预测值对比')
plt.plot(predict_y[:50], 'ro-', label='预测值')
plt.plot(test_y[:50], 'go-', label='真实值')
plt.legend()
plt.show()
9.集成模型Voting
Voting可以简单理解为将各个模型的结果加权平均,也是使用较多的一种集成模型。
代码如下:
model_voting = VotingRegressor(estimators=[('model_LR', model_LR),
('model_knn', model_knn),
('model_dtr', model_dtr),
('model_rfr', model_rfr),
('model_xgbr', model_xgbr)])
model_voting.fit(x_train, y_train)
# print("params: ", model_voting.get_params())
print("train score: ", model_voting.score(x_train, y_train))
print("test score: ", model_voting.score(x_test, y_test))
predict_y = evaluation(model_voting)
输出结果:
train score: 0.9572901767964346
test score: 0.8964163648799375
MAE: 1.08
MSE: 11.44
RMSE: 3.38
绘图:
plt.figure(figsize=(10,10))
plt.title('集成模型voting-真实值预测值对比')
plt.plot(predict_y[:50], 'ro-', label='预测值')
plt.plot(test_y[:50], 'go-', label='真实值')
plt.legend()
plt.show()
10.Tensorflow神经网络
使用Tensorflow前需要安装,本文使用的是tensorflow2.0.0版本。
为了使模型快速收敛,首先需要将数据标准化。
代码如下:
scaler = StandardScaler()
x_train_scaled = scaler.fit_transform(x_train)
x_test_scaled = scaler.transform(x_test)
train_x = np.array(x_train_scaled)
test_x = np.array(x_test_scaled)
train_y = np.array(y_train)
test_y = np.array(y_test)
# 1、模型初始化
model_tf = tf.keras.Sequential()
# 2、添加隐藏层,并设置激活函数,这里我们用relu
model_tf.add(layers.Dense(128, activation='relu'))
model_tf.add(layers.Dense(64, activation='relu'))
model_tf.add(layers.Dense(8, activation='relu'))
model_tf.add(layers.Dense(4, activation='relu'))
model_tf.add(layers.Dense(1, activation='relu'))
# 3、初始化输入的shape,189为输入的189维特征
model_tf.build(input_shape =(None,189))
# 4、编译模型
model_tf.compile(optimizer=tf.keras.optimizers.RMSprop(0.001),
loss=tf.keras.losses.mean_squared_error,
metrics=['mse', 'mae'])
# 5、模型训练
history = model_tf.fit(train_x, train_y, epochs=200, batch_size=128,
validation_split = 0.2, #从测试集中划分80%给训练集
validation_freq = 1) #测试的间隔次数为1
# 获取模型训练过程
model_tf.summary()
history_dict = history.history
loss_values = history_dict['loss']
mae=history_dict["mae"]
mse=history_dict["mse"]
val_loss = history_dict['val_loss']
val_mae = history_dict['val_mae']
val_mse = history_dict['val_mse']
epochs = range(1, len(loss_values) + 1)
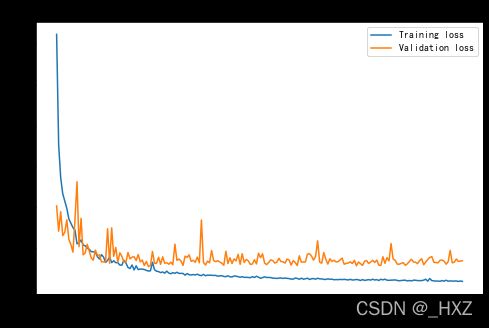
plt.figure(figsize=(8,5))
plt.plot(range(1, len(loss_values) + 1), loss_values, label = 'Training loss')
plt.plot(range(1, len(val_loss) + 1), val_loss, label = 'Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
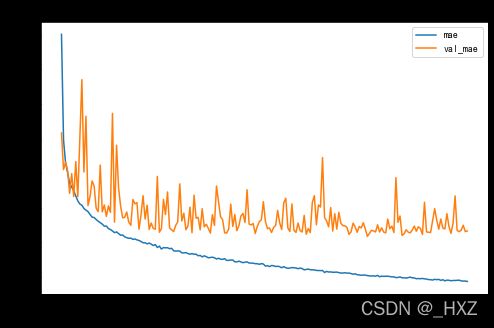
模型MAE:
plt.figure(figsize=(8,5))
plt.plot(range(1, len(mae) + 1), mae, label = 'mae')
plt.plot(range(1, len(val_mae) + 1), val_mae, label = 'val_mae')
plt.title('mean_absolute_error')
plt.xlabel('Epochs')
plt.ylabel('error')
plt.legend()
plt.show()
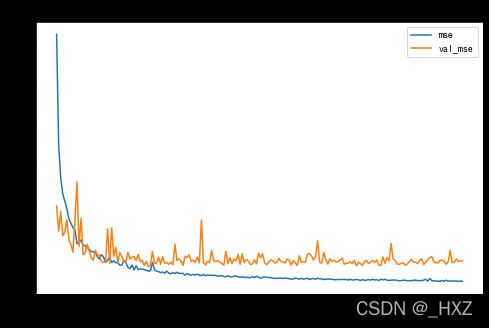
plt.figure(figsize=(8,5))
plt.plot(range(1, len(mse) + 1), mse, label = 'mse')
plt.plot(range(1, len(val_mse) + 1), val_mse, label = 'val_mse')
plt.title('mean_squre_error')
plt.xlabel('Epochs')
plt.ylabel('error')
plt.legend()
plt.show()
ypred = model_tf.predict(test_x)
mae = mean_absolute_error(test_y, ypred)
mse = mean_squared_error(test_y, ypred)
rmse = sqrt(mse)
print("MAE: %.2f" % mae)
print("MSE: %.2f" % mse)
print("RMSE: %.2f" % rmse)
输出结果:
MAE: 0.94
MSE: 24.03
RMSE: 4.90
11.各模型结果
| 模型名称 | MAE | MSE | RMSE | Train R2 | Test R2 |
|---|---|---|---|---|---|
| 线性回归 | 1.97 | 25.9 | 5.09 | 0.82 | 0.76 |
| KNN | 1.35 | 23.3 | 4.83 | 0.87 | 0.78 |
| 决策树 | 2.09 | 23.9 | 4.89 | 0.84 | 0.78 |
| 随机森林 | 0.88 | 10.99 | 3.32 | 0.98 | 0.90 |
| XGBoost | 0.88 | 11.88 | 3.45 | 0.98 | 0.89 |
| Voting | 1.08 | 11.44 | 3.38 | 0.95 | 0.89 |
| 神经网络 | 0.94 | 24.0 | 4.90 | 0.98 | 0.78 |
从上表可以看出,随机森林模型的整体表现最好。当然,这不代表最优结果,因为上述7种模型都没有进行调参优化,经过调参后的各个模型效果还有可能提升。
三、重要特征筛选
为了提升模型效果也可以对数据做特征筛选,这里可以通过相关系数分析法,将影响二手车售价的特征与售价做相关系数计算,pandas包很方便的集成了算法,并且可以通过seaborn、matplotlib等绘图包将相关系数用热力图的方式可视化。
# 这里的列取final_data中,除0-1和独热编码形式的数据
corr_cols = list(data.columns[:28]) + list(data.columns[43:49])
test_data = data[corr_cols]
test_data_corr = test_data.corr()
price_corr = dict(test_data_corr.iloc[0])
price_corr = sorted(price_corr.items(), key=lambda x: abs(x[1]), reverse=True)
# 输出按绝对值排序后的相关系数
print(price_corr)
输出结果,除"售价"外,共有33个特征:
[('售价', 1.0),
('新车售价', 0.7839935301900343),
('最大功率(kW)', 0.7117612690884588),
('最大马力(Ps)', 0.7110554212212731),
('最大扭矩(N·m)', 0.696952631401139),
('最高车速(km/h)', 0.5419965777866631),
('排量(mL)', 0.5330405118740592),
('排量(L)', 0.5308107362792799),
('整备质量(kg)', 0.49194473580917225),
('官方0-100km/h加速(s)', -0.48176542342318535),
('宽度(mm)', 0.4714397275896106),
('轴距(mm)', 0.46166756230018036),
('气缸数(个)', 0.4454272911508132),
('油箱容积(L)', 0.437777686409757),
('后轮距(mm)', 0.38050056092464896),
('长度(mm)', 0.3713764530321577),
('前轮距(mm)', 0.3620381932871346),
('最大扭矩转速(rpm)', -0.3350318499883131),
('注册日期差(天)', -0.2737947095245184),
('出厂日期差(天)', -0.2598892184068559),
('工信部综合油耗(L/100km)', 0.21117598576704852),
('行驶里程', -0.15837809707633024),
('最大功率转速(rpm)', -0.14929627599693607),
('行李厢容积(L)', 0.1303796302281349),
('每缸气门数(个)', 0.08610716158708019),
('压缩比', 0.0820485577972737),
('车门数', -0.05405277879497536),
('高度(mm)', 0.04866102899154555),
('商业险过期日期差(天)', -0.047366786391213236),
('交强险过期日期差(天)', -0.04465347803879652),
('车船税过期日期差(天)', -0.03694367077131783),
('载客/人', -0.03234487106605593),
('最小离地间隙(mm)', 0.027822359248097703),
('座位数', 0.016036623933084658)]
绘制热力图:
price_corr_cols = [ r[0] for r in price_corr ]
price_data = test_data_corr[price_corr_cols].loc[price_corr_cols]
plt.figure(figsize=(15, 10))
plt.title("相关系数热力图")
ax = sns.heatmap(price_data, linewidths=0.5, cmap='OrRd', cbar=True)
plt.show()

为了验证相关系数分析出来的重要特征是否对模型有效,我们将模型效果最好的随机森林模型的前33个重要特征输出。
feature_important = sorted(
zip(x_train.columns, map(lambda x:round(x,4), model_rfr.feature_importances_)),
key=lambda x: x[1],reverse=True)
for i in range(33):
print(feature_important[i])
输出结果:
('新车售价', 0.5435)
('最大马力(Ps)', 0.0928)
('注册日期差(天)', 0.077)
('最大扭矩(N·m)', 0.0547)
('最大功率(kW)', 0.05)
('行驶里程', 0.0406)
('出厂日期差(天)', 0.0187)
('高度(mm)', 0.0128)
('驻车制动类型_手刹', 0.0107)
('最大功率转速(rpm)', 0.0098)
('宽度(mm)', 0.007)
('轴距(mm)', 0.0059)
('工信部综合油耗(L/100km)', 0.0052)
('最大扭矩转速(rpm)', 0.0043)
('长度(mm)', 0.0042)
('助力类型_电动助力', 0.0041)
('后轮距(mm)', 0.0038)
('整备质量(kg)', 0.0038)
('挡位个数_5', 0.0035)
('行李厢容积(L)', 0.0027)
('最高车速(km/h)', 0.0026)
('官方0-100km/h加速(s)', 0.0026)
('油箱容积(L)', 0.0026)
('前轮距(mm)', 0.0024)
('压缩比', 0.0023)
('排量(mL)', 0.0021)
('排量(L)', 0.0019)
('上坡辅助', 0.0015)
('日间行车灯', 0.0013)
('商业险过期日期差(天)', 0.0013)
('最小离地间隙(mm)', 0.0012)
('挡位个数_6', 0.0012)
('交强险过期日期差(天)', 0.0011)
将相关系数分析出来的重要特征集合与随机森林的前33个重要特征取交集,并输出有多少个重复的特征。
f1_list = []
f2_list = []
for i in range(33):
f1_list.append(feature_important[i][0])
for i in range(1, 34):
f2_list.append(price_corr[i][0])
cnt = 0
for i in range(33):
if f1_list[i] in f2_list:
print(f1_list[i])
cnt += 1
print("共有"+str(cnt)+"个重复特征!")
输出结果:
新车售价
最大马力(Ps)
注册日期差(天)
最大扭矩(N·m)
最大功率(kW)
行驶里程
出厂日期差(天)
高度(mm)
最大功率转速(rpm)
宽度(mm)
轴距(mm)
工信部综合油耗(L/100km)
最大扭矩转速(rpm)
长度(mm)
后轮距(mm)
整备质量(kg)
行李厢容积(L)
最高车速(km/h)
官方0-100km/h加速(s)
油箱容积(L)
前轮距(mm)
压缩比
排量(mL)
排量(L)
商业险过期日期差(天)
最小离地间隙(mm)
交强险过期日期差(天)
共有27个重复特征!
结果表明,相关系数分析出来的重要特征对模型的效果是有效的。数据分析的魅力就在于通过统计学习的方法,能在模型训练前得到有价值的信息,甚至能挖掘出意想不到的结论。
在我看来,模型预测结果的好坏,最重要的是数据预处理,其次是特征工程和特征筛选,而模型及调参只是找到一个无限接近正确答案的工具。
结语
数据分析、数据挖掘以及模型训练还有很多没有学到的,我也只是将我个人学习理解到的东西展现出来,为朋友们抛砖引玉,希望朋友们在我的baseline方法中,创造更完美的答案。