机器学习基础整理(第1章) - 什么是机器学习?
文章目录
- 总体思路
- 常见机器学习场景
- 学习任务的分类
- 任务
-
- 分类 (Classfication)
- 回归 (Regression)
- 转录 (Transcription)
- 机器翻译 (Machine Translation)
- 结构化输出 (Structured Output)
- 异常检测 (Anomaly Detection)
- 合成和采样 (Synthesis and Sampling)
- 缺失值的插补 (Imputation of Missing Values)
- 除噪 (Denoising)
- 密度估计或概率函数估计 (Density Estimation or Probability Function Estimation)
- 性能 (Performance)
- 经验 (Experience)
- 数据表示 (Data Representation)
- 例子: 线性回归
-
- 数据表示
- 性能衡量
- 模型的容量,过拟合和欠拟合
- PAC学习框架 (PAC Learning Framework)
总体思路
- 机器学习是从数据从提取模式的自动化过程。
- 机器学习是通过电脑编程并使用 实例数据 (example data) 或者 过去经验 (past experience) 来优化性能标准。
- 一般来说,机器学习算法学习将 一个空间的"单元" 映射到另一个空间的"单元" 的函数。
- 一个学习算法可以从数据中进行学习。
- 学习算法通常包括: 优化 (optimization),损失函数 (cost function),一个模型 (model) 和一个数据集 (dataset)。
- 模型通常定义了一些参数 (parameters),而学习就是通过训练数据 (training data) 优化这些参数的过程。
- 模型 可以是 预测型 (predictive - 从新的或未来数据中做预测) 或 描述型 (descriptive - 从数据中得到知识或理解) 或两者结合。
什么是机器学习?
“机器学习算法通过搜索一组 可能的模型 来选择最能捕捉 数据集中描述性特征 和 目标特征 之间关系的模型(这只是故事的一部分,而现在已经有丰富的理论可以充分解释它)”
什么是学习?
“一个 被称为 从经验 E E E 中 学习关于 某类任务 T T T 和 性能度量 P P P,如果它在 T T T 中由 P P P 度量的任务的性能随着经验而提高 的计算机程序”
机器学习感兴趣的任务: “很难用 人类编写和设计的固定程序 解决的任务”
注: 学习的过程不是任务,学习只是获得执行任务能力的一种手段。
常见机器学习场景
- 监督型学习 (Supervised Learning): 学习器 接收一组 标记的示例 (labelled example) 作为训练数据,并对所有 未见过的点 进行预测。 例如,我们在分类 (classification)、回归 (regression) 和排名 (ranking) 问题中会遇到这种情况。
- 无监督学习 (Unsupervised Learning):学习器专门接收 未标记的数据 (unlabelled data),并对所有看不见的点进行预测。 聚类 (clustering) 和降维 (dimensionality reduction) 就是例子。
- 半监督学习 (Semi-supervised Learning):学习器接收由 标记数据和未标记数据 组成的训练样本,并对所有看不见的点进行预测。 这通常用于 未标记数据容易获得 但 标记数据获取成本高 的情况。
- 转导推理 (Transductive Inference):类似于半监督学习,学习者接收一个 标记的训练样本 以及一组 未标记 的测试点。 转导推理的目标是仅预测这些 特定测试点 的标签。(如: 当前具有 少量标注 的样本,使用KNN算法预测样本类别。训练样本是少量已经标注(A、B、C)的点,而其它大部分的点都是未标注的,通过已标记的点可以给这些从属于同个簇的未标记的点进行标记)
- 在线学习 (On-line Learning):此场景涉及多轮,并且 训练和测试阶段 是混合的。 在每一轮中,学习者都会收到一个 未标记的训练点,进行预测并产生损失。 目标是最小化所有轮次的 累积损失 (cummulative loss)。
- 强化学习 (Reinforcement Learning):训练和测试阶段 混合在一起。 学习者 通过主动与环境交互并有时也会 影响环境 来收集信息,以便为每个动作立即获得奖励。 目标是随着时间的推移 最大化奖励 (maximize the reward)。 这个学习场景与动态规划有关。
- 主动学习 (Active Learning):学习者通过 查询oracle 从 新的项 请求标签,自适应地 或 交互式 地收集训练示例。 其目标是实现与 标准监督学习场景 相当的性能。
学习任务的分类
- 分类 (Classification): 为每个项分配一个类别。
- 回归 (Regression): 为每个项预测一个值。
- 排序 (Ranking): 依据某种标准来对项进行排序,如网页搜索。
- 聚类 (Clustering): 将项划分为同质区域 (homogeneous regions)
- 降维 (Dimensionality reduction) 或流形学习 (manifold learning) - 将 项 的初始表示转换为这些 项 的较低维度,同时保留项的一些属性。
任务
根据机器学习系统应如何处理 示例描述 的任务。
示例 (example) 是从机器学习系统将处理的某些对象或事件中 定量测量(quantitatively measure) 的特征集合 (collection of features)。
分类 (Classfication)
任务需要 指定某些输入 属于 k 个类别中的哪一个。
从数据中学习以下形式的函数:
f : R n → { 1 , . . . , k } f: \R^n \to \{1, ..., k\} f:Rn→{1,...,k}
y = f ( x ) y=f(x) y=f(x) 将分配一个类别 y y y 给 特征 x x x。
函数应也能输出一个类别的概率分布 (probability dirstribution)。
回归 (Regression)
根据给定的输入 预测 数值输出。
从数据中学习以下形式的函数:
f : R n → R f: \R^n \to \R f:Rn→R
和分类任务不同,分类任务要求输出 是 分类数据类型。
转录 (Transcription)
需要观察某种数据的 相对非结构化的表示 (relatively unstructured representation) 并将其转录成离散的文本形式 (discrete textual form)
从数据中学习以下形式的函数:
f : R n → A k ( m ) f: \R^n \to \mathbb{A}^{k(m)} f:Rn→Ak(m)
其中 A \mathbb{A} A 是一些语言字母,如英文等, k ( m ) k(m) k(m) 是一些可变数字,表示 字母表的可变长度并取决于应用程序,其中语音识别就是一个例子。
机器翻译 (Machine Translation)
需要将某种语言的符号(或字母)序列转换为另一种语言的符号(字母)序列。
从数据中学习以下形式的函数:
f : A x k ( n ) → A y k ( m ) f: \mathbb{A}^{k(n)}_x \to \mathbb{A}^{k(m)}_y f:Axk(n)→Ayk(m)
其中 A x \mathbb{A}_x Ax 是源语言字母表 (如英语或普通话), k ( m ) k(m) k(m)是一些可变数字,其代表了字母表的可变长度, A y \mathbb{A}_y Ay 是 目标语言字母表 (如德语,法语等)。
结构化输出 (Structured Output)
此类任务包括转录和翻译
需要将输入转换为 能建模成数据结构 的输出,该数据结构包含 元素之间具有重要关系 的多个值
示例包括 提供 给定图片 或 给定视频中 正在执行的活动的文本描述。
异常检测 (Anomaly Detection)
需要筛选一组事件或对象,并将其中一些标记为不寻常或非典型 (unusal or atypical)。
异常对象属于 与其他事件或对象 非常不同的概率分布。
如何估计分布以及如何测量分布之间的距离?
合成和采样 (Synthesis and Sampling)
需要生成与 训练数据中的示例 相似的 新示例。
尽可能地让所需的输出具有指定的边界结构 (specific structure with bound)。
示例:从各种口音的书面文本中合成语音。
挑战: 给定一个嫌疑人的描述,是否能让机器生成此人的画像?
应用: 生成对抗网络 (Generative Adversarial Network - GAN)
缺失值的插补 (Imputation of Missing Values)
此任务要求在给定的示例中,提供缺失项的预测,其中 x ∈ R n x \in \R^n x∈Rn
除噪 (Denoising)
该任务要求从 损坏带噪 的版本 x ‾ \overline{x} x 预测 干净无噪声 的示例 x x x
这与预测条件概率分布 p ( x ∣ x ‾ ) p(x|\overline{x}) p(x∣x) 相同。

密度估计或概率函数估计 (Density Estimation or Probability Function Estimation)
要求学习函数:
p m o d e l : R n → R p_{model}: \R^n \to \R pmodel:Rn→R
其中 p m o d e l p_{model} pmodel 是提取示例的空间中的 概率密度函数 或者 概率质量函数。
许多机器学习任务要求概率密度的估计。
性能 (Performance)
我们需要使用性能的量化方式 (quantitative measures) 来评估机器学习算法的能力。
性能的衡量方式基于不同任务,如:
- 准确率 (Accuracy)
- 误差率 (Error Rate)
- 精确度 (Precision)
- 召回率 (Recall)
必须选择能够匹配系统的期望行为 的性能度量。
经验 (Experience)
机器学习算法所接触的经验可以是 有监督的,也可以是无监督的。
- 无监督学习算法的经验 包含 许多特征的数据集,并且需要从数据集中学习有用的属性
本质上,给定 随机向量 x x x 的几个例子,隐式或显式地学习其概率分布 p ( x ) p(x) p(x)。 - 监督学习算法经验 包含 许多特征 以及 与每个示例相关的 标签(或目标)的数据集
本质上,给定随机向量 x x x 和相关标签 y y y 的几个示例,学习去估计 条件分布 p ( y ∣ x ) p(y|x) p(y∣x) (conditional distribution)
数据表示 (Data Representation)
我们可以设计矩阵,使得 X ∈ R N × P X \in \R^{N × P} X∈RN×P
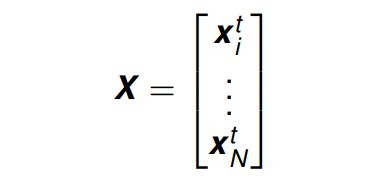
其代表了 拥有 P P P 个特征的 N N N 个示例 (或观察或样本)。
其第 i i i 个特征向量的表示如下:
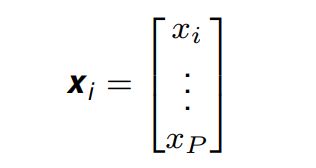
其中 x i x_i xi 是被测量的特征值。
在示例中的 特征数量不相等 的情况下,也可以使用集合:
{ x ( 1 ) , x ( 2 ) , . . . , x ( m ) } \{x^{(1)}, x^{(2)}, ..., x^{(m)} \} {x(1),x(2),...,x(m)}
以上代表了拥有 m m m 个元素的集合,且其中元素的特征并不是数量一致的。
例子: 线性回归
数据表示
线性回归: 构建一个能输入向量 x ∈ R P x \in \R^P x∈RP 并 预测标量 y ∈ R y \in \ R y∈ R 的值 的系统。
线性回归模型的输出是输入的线性函数。

其中 ω ∈ R P \omega \in \R^P ω∈RP 是参数的向量,他们决定了每个特征如何影响最终的预测,因此任务就变成了通过计算式子右侧来 预测 左边的值。
性能衡量
我们如何衡量性能 P P P ?
在回归问题中,我们将拥有以矩阵 X X X 代表的数据集。数据集被分成两部分,测试集 X ( t e s t ) X^{(test)} X(test) 和训练集 X t r a i n i n g X^{training} Xtraining。我们从 X t r a i n i n g X^{training} Xtraining中学习出模型,并在 X t e s t X^{test} Xtest 中测试性能。
在例子中,我们使用 均方误差 (mean squared error) 作为性能衡量。
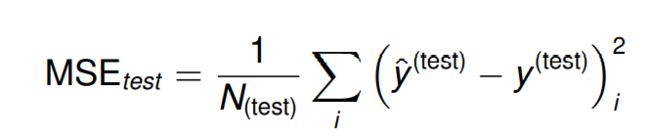
训练的过程包含了寻找能够使 M S E t r a i n i n g MSE_{training} MSEtraining 最小 的 权重向量(weight vector) ω \omega ω

微分 (differentiating) 并等于0能得到:
模型的容量,过拟合和欠拟合
泛化性 (Generalization) 是机器学习的关键。经过训练的算法 应该能在 新的 和 之前未见过的输入 表现良好。
我们进行优化以减少训练误差,但我们 也希望 泛化误差 generalization error(测试误差 test error)低。因为这也是 对于新输入 的预期错误。
重要提示:期望 是从 我们期望系统在实践中遇到的输入分布 中得出的 不同可能输入中 得出的。

因为 假设 “由数据生成过程 (data generating process) 生成的独立且同分布的随机变量 (i.i.d - independent and identically distributed random variates)” 的存在, 因此上述是可能的。
决定 机器学习算法能表现如何的 因素是其能够:
- 使得训练误差小。
- 同时也要使训练和测试误差之间的差距小。
欠拟合 (Underfitting): 模型无法在训练集上获得足够小的训练误差。
过拟合 (Overfitting): 训练集和测试集误差之间的差距过大。
容量 (Capacity):模型拟合各种函数的能力。容量低的模型可能很难拟合数据集。例如我们用一个一次函数做线性回归,很显然,复杂分布下的数据就难以表示了。但容量高的模型则可能会导致过拟合。
通过 改变容量 或 增加训练样本的数量 来控制 欠拟合和过拟合
- 通过选择 假设空间 (hypothesis space)(允许学习算法选择的函数集作为可能的解决方案)来改变容量, 这相当于增加/减少特征的数量。
- 也可以通过增加示例数据的数量来避免过拟合
从示例数据中训练的学习算法的三种权衡:
- 拟合数据的假设复杂性(complexity of hypothesis),即假设类的容量 (capacity of the hypothesis class)。
- 可用的训练数据数量。
- 对新示例的泛化误差。
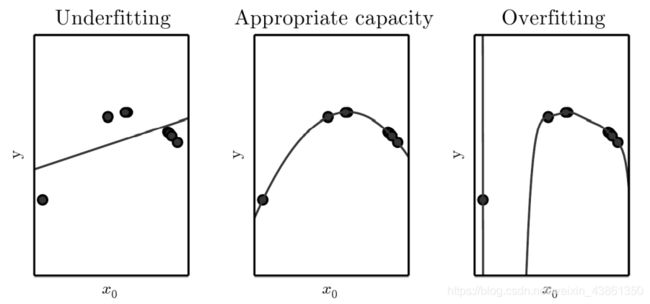
三个模型适用于通过 随机采样 x x x 生成的 合成数据 (synthetic data) 示例,并从二次方程计算 y y y 的相应值。
- 第一张图: 拟合线性函数,但由于无法捕捉曲率,因此欠拟合。
- 第二张图: 拟合二次函数,其很好地概括了看不见的数据,模型没有明显的欠拟合或过拟合。
- 第三张图: 拟合 9 次多项式,模型有 过拟合 问题。曲线的奇怪结构值得注意,这是因为它试图拟合所有训练数据。
PAC学习框架 (PAC Learning Framework)
首先进行一些定义:
- 使用 X X X 代表所有可能的示例或实例,这被称为输入空间 (input space)。
- 使用 y y y 代表所有可能的标签或目标值,在下面的解释中,假设 y = { 0 , 1 } y = \{0, 1\} y={0,1},这代表了我们要讨论一个二元分类问题。
- 使用 c : X → y c: X \to y c:X→y 代表一个概念 (concept),这是从 X X X 到 y y y 的映射,我们可以将 c c c 标识为 X X X 的子集,在该子集中其值是1。
- 讨论中,我们假设 示例 是符合 在一些 固定但未知 的分布 D D D 中 (i.i.d 独立且同分布) 的。
学习问题:
学习者考虑一组 固定可能概念 H H H,被称为 假设集 (hypothesis set),其与 C C C 不一致。他接收到一组根据分布 D D D 通过 i.i.d 抽取的 样本 S = { x 1 , . . . , x m } S=\{x_1, ..., x_m\} S={x1,...,xm} 和 标签 ( c ( x 1 ) , . . . c ( x m ) ) (c(x_1), ... c(x_m)) (c(x1),...c(xm)),其是基于某个特定目标概念 c ∈ C c \in C c∈C 来学习的。学习者的任务是使用 带标签的样本 S S S 来选择一个 对于概念 c c c 拥有最小泛化误差的假设 h s ∈ H h_s \in H hs∈H。
泛化误差 (generalization error):
给定一个假设 h ∈ H h \in H h∈H,一个目标概念 c ∈ C c \in C c∈C,以及一个潜在的分布 D D D, h h h 的泛化误差或风险被定义为:
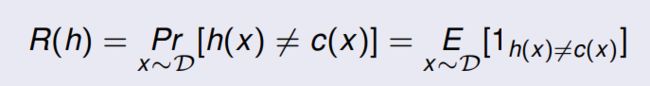
其中, 1 ω 1_\omega 1ω 是事件 ω \omega ω 的指示函数。而 E x ∼ D \mathop{E}\limits_{x \sim D} x∼DE 是从 分布 D D D 中得出的对 x x x 的期望。
但由于 分布 D D D 和 概念 c c c 对于学习者都不可知,因此我们可以不衡量泛化误差,转而衡量经验误差。
经验误差 (Empirical error)
给定一个假设 h ∈ H h \in H h∈H,一个目标概念 c ∈ C c \in C c∈C,以及样本 S = ( x 1 , . . . , x m ) S = (x_1, ..., x_m) S=(x1,...,xm),则 h h h 的经验误差或风险被定义为:
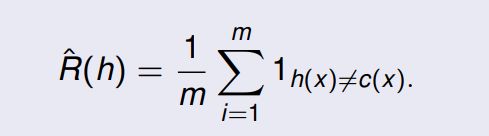
经验误差是在样本 S S S 中的平均误差。
对于一个固定假设 h ∈ H h \in H h∈H,基于 i.i.d 样本 S S S 的经验误差的期望等于泛化误差:
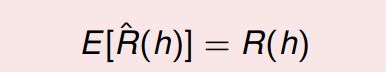
PAC 学习框架提供了对训练样本大小 m m m, 训练与真实错误之间的差距, 假设空间 H H H 的复杂性以及我们对这种关系的置信度(至少 1 − δ 1 - δ 1−δ)的理论限制。
PAC 即 Probably Approximately Correct,也就是 可能大概正确。
PAC学习框架:
若存在一个算法 A A A 以及一个多项式函数 p o l y ( , , , , ) poly(, , , ,) poly(,,,,) 使得任意 ϵ > 0 \epsilon \gt 0 ϵ>0 以及 δ > 0 \delta \gt 0 δ>0,且对于所有在 X X X 上的分布 D D D 以及对于任意 目标概念 c ∈ C c \in C c∈C,下式在任意 样本大小 m ≥ p o l y ( 1 / ϵ , 1 / δ , n , s i z e ( c ) ) m \ge poly(1/\epsilon, 1/\delta, n, size(c)) m≥poly(1/ϵ,1/δ,n,size(c)) 时满足,则一个 概念类 C C C 可以被称为 PAC可学习 (PAC-learnable)。:
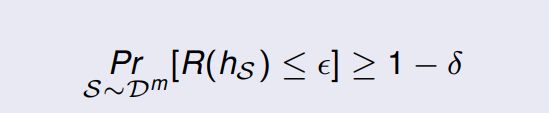
若算法 A A A 之后在 p o l y ( 1 / ϵ , 1 / δ , n , s i z e ( c ) ) poly(1/\epsilon, 1/\delta, n, size(c)) poly(1/ϵ,1/δ,n,size(c)) 的复杂度中运行,则 C C C 被认为是高效PAC可学习的 (efficiently PAC-learnable)。算法 A A A (若存在) 则被称为一个 C C C 的 PAC学习算法。
在上面的定义中, n n n 与任何元素 x ∈ X x ∈ X x∈X 的计算表示的成本上限 ( O ( n ) O(n) O(n)) 相关联。 同样, s i z e ( c ) size(c) size(c) 是 c ∈ C c ∈ C c∈C 的计算表示的最大成本。