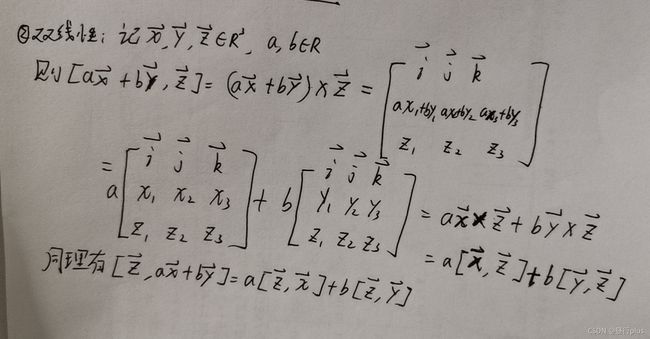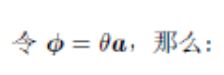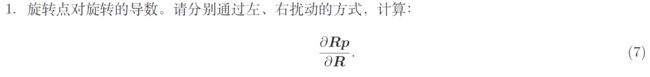视觉SLAM入门 -- 学习笔记 - Part3

2 群的性质

先看群的定义：

补充：
3. 解释什么是阿贝尔群。并说明矩阵及乘法构成的群是否为阿贝尔群。

阿贝尔群（Abel Group）又称交换群或可交换群，
它由自身的集合 G 和二元运算 * 构成。它除了满足一般的群公理，即运算的结合律、G 有单位元、所有 G 的元素都有逆元之外，还满足交换律公理。因为阿贝尔群的群运算满足交换律和结合律，群元素乘积的值与乘法运算时的次序无关。
plus:​ 矩阵即使是可逆矩阵，一般不形成在乘法下的阿贝尔群，因为矩阵乘法一般是不可交换的。但是某些矩阵的群是在矩阵乘法下的阿贝尔群 - 一个例子是 2x2 旋转矩阵的群。

3 验证向量叉乘的李代数性质

附： 自反性是指自己与自己的运算为零

4 推导SE(3) 的指数映射

课上给出了SO(3) 的指数映射推导，但对于SE(3)，仅介绍了结论，没有给出详细推导。请你完成SE(3) 指数映射部分，有关左雅可⽐的详细推导。

5 伴随

在SO(3) 和SE(3) 上，有⼀个东西称为伴随（Adjoint）。下⾯请你证明SO(3) 伴随的性质。

页面 https://math.stackexchange.com/questions/2190603/derivation-of-adjoint-for-so3

这个性质将在后⽂的Pose Graph 优化中⽤到。但是SE(3) 的证明较为复杂，不作要求。

完整的SO(3) 和SE(3) 性质见表1和表2。

6 轨迹的描绘

我们通常会记录机器⼈的运动轨迹，来观察它的运动是否符合预期。大部分数据集都会提供标准轨迹以供参考，如kitti、TUM-RGBD 等。这些⽂件会有各⾃的格式，但⾸先你要理解它的内容。记世界坐标系为W，机器⼈坐标系为C，那么机器⼈的运动可以⽤$T_{wc}$ 或$T_{cw}$ 来描述。现在，我们希望画出机器⼈在世界当中的运动轨迹，请回答以下问题：

1. 事实上，$T_{wc}$的平移部分即构成了机器⼈的轨迹。它的物理意义是什么？为何画出$T_{wc}$的平移部分就得到了机器⼈的轨迹？

答：$T_{wc}$代表机器人每个抽样时刻相对世界坐标系的位姿，因而其平移部分连起来便是机器人的轨迹

2. 我为你准备了⼀个轨迹文件（code/trajectory.txt）。该文件的每一行由若干个数据组成，格式为

draw_trajectory.cpp:

#include "sophus/se3.hpp"
#include 
#include 
#include 
#include 

// need pangolin for plotting trajectory
#include 


using namespace std;
using namespace Eigen;

// path to trajectory file
string trajectory_file = "./trajectory.txt";

// function for plotting trajectory, don't edit this code
// start point is red and end point is blue
void DrawTrajectory(vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>>);

int main(int argc, char **argv) {

    vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> poses;


    /// implement pose reading code
    // start your code here (5~10 lines)
    ifstream file(trajectory_file);
    if(!file){
        cerr << "trajectory " << trajectory_file << " not found !" <<endl;
    }
    while(!file.eof()){
        double time, tx, ty, tz, qx, qy, qz, qw;
        file >> time
             >> tx >> ty >> tz
             >> qx >> qy >> qz >> qw;
        Vector3d t(tx, ty, tz);
        Quaterniond q(qw, qx, qy, qz);
        q.normalize();
        Sophus::SE3d SE3(q, t);
        poses.push_back(SE3);
    }

    file.close();
    // end your code here

    // draw trajectory in pangolin
    DrawTrajectory(poses);
    return 0;
}

/***************************************************************************/
void DrawTrajectory(vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> poses) {
    if (poses.empty()) {
        cerr << "Trajectory is empty!" << endl;
        return;
    }

    // create pangolin window and plot the trajectory
    pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);
    glEnable(GL_DEPTH_TEST);
    glEnable(GL_BLEND);
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

    pangolin::OpenGlRenderState s_cam(
            pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
            pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
    );

    pangolin::View &d_cam = pangolin::CreateDisplay()
            .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
            .SetHandler(new pangolin::Handler3D(s_cam));


    while (pangolin::ShouldQuit() == false) {
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

        d_cam.Activate(s_cam);
        glClearColor(1.0f, 1.0f, 1.0f, 1.0f);

        glLineWidth(2);
        for (size_t i = 0; i < poses.size() - 1; i++) {
            glColor3f(1 - (float) i / poses.size(), 0.0f, (float) i / poses.size());
            glBegin(GL_LINES);
            auto p1 = poses[i], p2 = poses[i + 1];
            glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
            glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
            glEnd();
        }
        pangolin::FinishFrame();
        usleep(5000);   // sleep 5 ms
    }

}

CmakeList.txt:

cmake_minimum_required(VERSION 3.17)

project(PA3)

set(CMAKE_CXX_STANDARD 14)

include_directories( "/usr/include/eigen3" )

find_package(Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})

find_package(Pangolin REQUIRED)
include_directories(${Pangolin_INCLUDE_DIRS})

add_executable(draw_trajectory draw_trajectory.cpp)
target_link_libraries(draw_trajectory ${Pangolin_LIBRARIES})

代码输出：

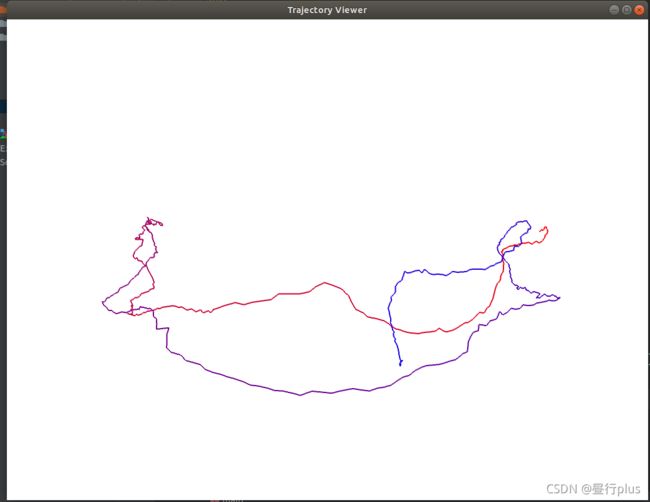
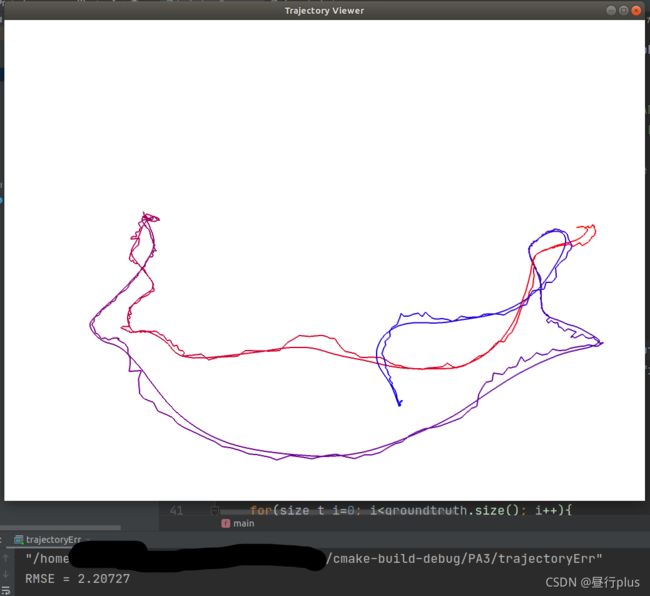
7 * 轨迹的误差

除了画出真实轨迹以外，我们经常需要把SLAM 估计的轨迹与真实轨迹相比较。下⾯说明比较的原理，请你完成比较部分的代码实现。

我为你准备了code/ground-truth.txt 和code/estimate.txt 两条轨迹。

请你根据上⾯公式，实现RMSE的计算代码，给出最后的RMSE 结果。

作为验算，参考答案为：2.207。

注：

1. 公式(7) 满足度量的定义：非负性、同一性、对称性、三角不等式，故形成距离函数。类似的，可以定义SO(3) 上的距离为：关于距离定义可以参见拓扑学或者泛函教材。
2. 实际当中的轨迹⽐较还要更复杂⼀些。通常ground-truth 由其他传感器记录（如vicon），它的采样频率通常⾼于相机的频率，所以在处理之前还需要按照时间戳对齐。另外，由于传感器坐标系不⼀致，还需要计算两个坐标系之间的差异。这件事也可以⽤ICP 解得，我们将在后⾯的课程中讲到。
3. 你可以⽤上题的画图程序将两条轨迹画在同⼀个图⾥，看看它们相差多少。

trajectoryErr.cpp：

//
// Created by daybeha on 17/10/2021.
//

#include "sophus/se3.hpp"
#include 
#include 
#include 
#include 

// need pangolin for plotting trajectory
#include 


using namespace std;
using namespace Eigen;

typedef vector<Sophus::SE3d, Eigen::aligned_allocator<Sophus::SE3d>> TrajectoryType;

// path to trajectory file
string groundtruth_file = "./groundtruth.txt";
string estimated_file = "./estimated.txt";

// function for plotting trajectory, don't edit this code
// start point is red and end point is blue
void DrawTrajectory(TrajectoryType , TrajectoryType );

TrajectoryType ReadTrajectory(string &trajectory_file);


int main(int argc, char **argv) {

    TrajectoryType groundtruth = ReadTrajectory(groundtruth_file);
    TrajectoryType estimated = ReadTrajectory(estimated_file);
    assert(!groundtruth.empty() && !estimated.empty());
    assert(groundtruth.size() == estimated.size());


    // caculate RMSE
    double rmse = 0;
    for(size_t i=0; i<groundtruth.size(); i++){
        Sophus::SE3d p1= groundtruth[i], p2= estimated[i];
        double e = (p1.inverse() * p2).log().norm();
        rmse += e * e;
    }
    rmse = sqrt(rmse/groundtruth.size());
    cout<<"RMSE = " << rmse <<endl;



    DrawTrajectory(groundtruth, estimated);
    return 0;
}

/**********************************************************************************/
void DrawTrajectory(TrajectoryType poses1, TrajectoryType poses2) {
    if (poses1.empty() || poses2.empty()) {
        cerr << "Trajectory is empty!" << endl;
        return;
    }

    // create pangolin window and plot the trajectory
    pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);
    glEnable(GL_DEPTH_TEST);
    glEnable(GL_BLEND);
    glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

    pangolin::OpenGlRenderState s_cam(
            pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
            pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
    );

    pangolin::View &d_cam = pangolin::CreateDisplay()
            .SetBounds(0.0, 1.0, pangolin::Attach::Pix(175), 1.0, -1024.0f / 768.0f)
            .SetHandler(new pangolin::Handler3D(s_cam));


    while (!pangolin::ShouldQuit()) {
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

        d_cam.Activate(s_cam);
        glClearColor(1.0f, 1.0f, 1.0f, 1.0f);

        glLineWidth(2);
        for (size_t i = 0; i < poses1.size() - 1; i++) {
            glColor3f(1 - (float) i / poses1.size(), 0.0f, (float) i / poses1.size());
            glBegin(GL_LINES);
            auto p1 = poses1[i], p2 = poses1[i + 1];
            glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
            glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
            glEnd();
        }

        for (size_t i = 0; i < poses2.size() - 1; i++) {
            glColor3f(1 - (float) i / poses2.size(), 0.0f, (float) i / poses2.size());
            glBegin(GL_LINES);
            auto p1 = poses2[i], p2 = poses2[i + 1];
            glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
            glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
            glEnd();
        }

        pangolin::FinishFrame();
        usleep(5000);   // sleep 5 ms
    }

}

TrajectoryType ReadTrajectory(string &trajectory_file){
    TrajectoryType poses;
    ifstream file(trajectory_file);
    if(!file){
        cerr << "trajectory " << trajectory_file << " not found !" <<endl;
    }
    while(!file.eof()){
        double time, tx, ty, tz, qx, qy, qz, qw;
        file >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw;
        Vector3d t(tx, ty, tz);
        Quaterniond q(qw, qx, qy, qz);
        Sophus::SE3d SE3(q, t);
        poses.push_back(SE3);
    }

    return poses;
}

CmakeList.txt:

cmake_minimum_required(VERSION 3.17)

project(PA3)

set(CMAKE_CXX_STANDARD 14)

include_directories( "/usr/include/eigen3" )

find_package(Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})

find_package(Pangolin REQUIRED)
include_directories(${Pangolin_INCLUDE_DIRS})

add_executable(useSophus useSophus.cpp)
add_executable(draw_trajectory draw_trajectory.cpp )
target_link_libraries(draw_trajectory ${Pangolin_LIBRARIES})
add_executable(trajectoryErr trajectoryErr.cpp)
target_link_libraries(trajectoryErr ${Pangolin_LIBRARIES})

代码输出：

补充：

提示：你可能需要用到上题的知识。

答：

设扰动$△R$对应的李代数为$\phi$， 则有
左扰动:
$$\begin{array}{rl}\frac{\partial Rp}{\partial R}& =\frac{\partial exp({\phi }^{\wedge })exp({\varphi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\partial \phi }\\ (泰勒展开)& \approx \underset{\phi \to 0}{\lim }\frac{(I+{\phi }^{\wedge })exp({\varphi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{{\phi }^{\wedge }Rp}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{-(Rp{)}^{\wedge }\phi }{\phi }\\ & =-(Rp{)}^{\wedge }\end{array}$$

---

右扰动:
$$\begin{array}{rl}\frac{\partial Rp}{\partial R}& =\frac{\partial exp({\varphi }^{\wedge })exp({\phi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\partial \phi }\\ (泰勒展开)& \approx \underset{\phi \to 0}{\lim }\frac{exp({\varphi }^{\wedge })(I+{\phi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{R{\phi }^{\wedge }p}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{-R{p}^{\wedge }\phi }{\phi }\\ & =-R{p}^{\wedge }\end{array}$$

答：

先看BCH的线性表达
$$\begin{array}{r}ln(exp({\varphi }_1^{\wedge })exp({\varphi }_2^{\wedge }){)}^{\vee }\approx \{\begin{array}{l}{J}_l({\varphi }_2{)}^{-1}{\varphi }_1+{\varphi }_2,当{\varphi }_1为小量\\ J_r({\varphi }_1{)}^{-1}{\varphi }_2+{\varphi }_1,当{\varphi }_2为小量\end{array}\end{array}$$

其中

$\varphi =\theta a,a为单位向量$
$J_l=J_{VSLA{M}_{P}80}=\frac{sin\theta }{\theta }I+(1-\frac{sin\theta }{\theta })a{a}^T+\frac{1-cos\theta }{\theta }{a}^{\wedge }$
$J_l^{-1}=\frac{\theta }{2}cot\frac{\theta }{2}I+(1-\frac{\theta }{2}cot\frac{\theta }{2})a{a}^T-\frac{\theta }{2}{a}^{\wedge }$
$J_r(\varphi )=J_l(-\varphi )$

还有两个重要公式，即SO(3) 伴随的性质：

$R{a}^{\wedge }{R}^T=(Ra{)}^{\wedge }$
$Rexp(a^{\wedge })R^T=exp((Ra{)}^{\wedge })$

---

同样设扰动$△R1$对应的李代数为$\phi$， 则有
左扰动：
$$\begin{array}{rl}\frac{\partial ln(R_1{R}_2{)}^{\vee }}{\partial R_1}& =\underset{\phi \to 0}{\lim }\frac{ln(exp({\phi }^{\wedge })R_1{R}_2{)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ (BCH)& \approx \underset{\phi \to 0}{\lim }\frac{J_l(ln(R_1{R}_2{)}^{\vee }{)}^{-1}\phi +ln(R_1{R}_2{)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{J_l(ln(R_1{R}_2{)}^{\vee }{)}^{-1}\phi }{\phi }\\ & =J_l(ln(R_1{R}_2{)}^{\vee }{)}^{-1}\end{array}$$
$$\begin{array}{rl}\frac{\partial ln(R_1{R}_2{)}^{\vee }}{\partial R_2}& =\underset{\phi \to 0}{\lim }\frac{ln(R_{1}exp({\phi }^{\wedge })R_2{)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{ln(R_1{R}_2{R}_2^{T}exp({\phi }^{\wedge })R_2{)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ (5伴随的公式4)& =\underset{\phi \to 0}{\lim }\frac{ln(R_1{R}_{2}exp((R_2^T\phi {)}^{\wedge }){)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ & \\ (BCH)& \approx \underset{\phi \to 0}{\lim }\frac{J_r(ln(R_1{R}_2{)}^{\vee }{)}^{-1}{R}_2^T\phi +ln(R_1{R}_2{)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{J_r(ln(R_1{R}_2{)}^{\vee }{)}^{-1}{R}_2^T\phi }{\phi }\\ & =J_r(ln(R_1{R}_2{)}^{\vee }{)}^{-1}{R}_2^T\end{array}$$

---

右扰动：
$$\begin{array}{rl}\frac{\partial ln(R_1{R}_2{)}^{\vee }}{\partial R_1}& =\underset{\phi \to 0}{\lim }\frac{ln(R_{1}exp({\phi }^{\wedge })R_2{)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{ln(R_{1}exp({\phi }^{\wedge })R_1^T{R}_1{R}_2{)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ (5伴随的公式4)& =\underset{\phi \to 0}{\lim }\frac{ln(exp((R_1\phi {)}^{\wedge })R_1{R}_2{)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ & \\ (BCH)& \approx \underset{\phi \to 0}{\lim }\frac{J_l(ln(R_1{R}_2{)}^{\vee }{)}^{-1}{R}_1\phi +ln(R_1{R}_2{)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{J_l(ln(R_1{R}_2{)}^{\vee }{)}^{-1}{R}_1\phi }{\phi }\\ & =J_l(ln(R_1{R}_2{)}^{\vee }{)}^{-1}{R}_1\end{array}$$
$$\begin{array}{rl}\frac{\partial ln(R_1{R}_2{)}^{\vee }}{\partial R_2}& =\underset{\phi \to 0}{\lim }\frac{ln(R_1{R}_{2}exp({\phi }^{\wedge }){)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ (BCH)& \approx \underset{\phi \to 0}{\lim }\frac{J_r(ln(R_1{R}_2{)}^{\vee }{)}^{-1}\phi +ln(R_1{R}_2{)}^{\vee }-ln(R_1{R}_2{)}^{\vee }}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{J_r(ln(R_1{R}_2{)}^{\vee }{)}^{-1}\phi }{\phi }\\ & =J_r(ln(R_1{R}_2{)}^{\vee }{)}^{-1}\end{array}$$

参考：

https://blog.csdn.net/weixin_42361804/article/details/113307927
https://blog.csdn.net/weixin_44218240/article/details/105793559?spm=1001.2014.3001.5501
https://blog.csdn.net/qq_21830903/article/details/95209007
https://blog.csdn.net/weixin_41074793/article/details/84853291?spm=1001.2014.3001.5501
https://github.com/gaoxiang12/slambook2
深蓝学院-视觉SLAM十四讲-第三章作业
视觉slam学习笔记以及课后习题《第三讲李群李代数》

从零手写VIO——（一）Introduction
视觉SLAM十四讲学习笔记（四）李群和李代数