【相机标定与三维重建原理及实现】学习笔记1——相机模型数学推导详解

---

前言

由于本人近期正在展开数字图像相关技术用于测量材料形变方向的研究，既然涉及到使用图像处理参与到测量或检测研究当中，就肯定避不开构建物空间上的任意一点与相机所拍摄到的图像上一点之间的数学关系及数学模型。之前有过标定经验的我只是单纯的使用别人封装好的函数，如今仔细推导过后才发现其中奥秘所在。我认为想要在一个技术上有所创新，最核心的还是能够将其学的透彻，我希望将自己作为一个初学者学习和推导该原理的过程记录下来，也方便之后每一个涉足该领域知识的人能更清晰更快的应用这些知识。

本文所写的内容主要参考《学习OpenCV 3 》¹以及 大奥特曼打小怪兽大佬的博客第六节、双目视觉之相机标定²。但是本文的讲解思路会稍有不同，同时也会更偏向数学推导。如果本文对你的帮助不大，建议可以看一下提到的书籍与博客，可以提供一些不同角度的讲解。

如果您对于标定第一次接触，我希望您可以带着下面这两个问题在本文的推导中一起思考：

1. 为什么要进行标定？
2. 标定到底是在计算什么东西？

本专栏目录：

1. 【相机标定与三维重建原理及实现】学习笔记1——相机模型数学推导详解
2. 【相机标定与三维重建原理及实现】学习笔记2——标定的算法与方法

文章中的图大部分都是我自己绘制的，之后写论文会用到，所以目前请不要盗用于商业用途，谢谢！

---

由于标定的主要目的是建立图像与实际被摄物体的变换关系，因此我们首先需要了解的是照相机系统数学模型——小孔成像模型。

一.小孔成像模型

对于任意一个折射型光路的照相机系统，无论其使用的镜头透镜组合有多么复杂，其都可以被简化的看做一个凸透镜，而光线通过凸透镜的光心，其光路不会发生偏折。因此照相机系统可以看做是一个小孔成像的模型，如下图所示

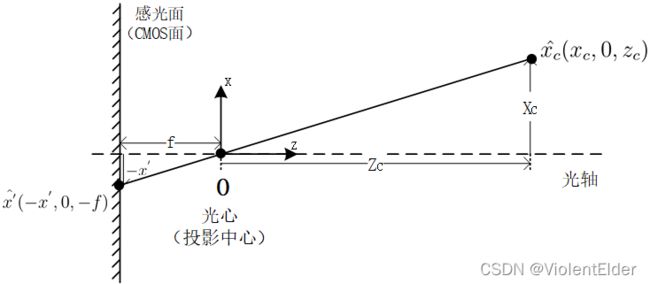
整个数学模型的坐标系建立在光心$O$上，其中$\widehat{x_c}$是物空间的一点，其发出或反射的光经过光心$O$后会投影到相机的感光面上，像点为$\widehat{x^{{}^{\prime }}}$，相机感光面到系统光心的距离为焦距$f$，如此一来根据相似三角形的公式可以得到
$$-\frac{x^{{}^{\prime }}}{f}=\frac{x_c}{z_c}$$而这里的负号也表示了，此时获得的是一个倒立的像。

由于当前关系式中存在负号，而且通常相机输出给我的图像都是已经做了上下翻转才输出的，为符合认知以及简便计算，我们可以将这个感光面绕投影中心顺时针旋转180°，将其移动到光心前$f$的位置，建立一个新的平面，而这个平面也就是计算机视觉当中所采用模型的像面（Image Plane），其与光轴的焦点也称为“主点”（Principal Point）。这样一来小孔成像的模型就变为了如下图所示的样子

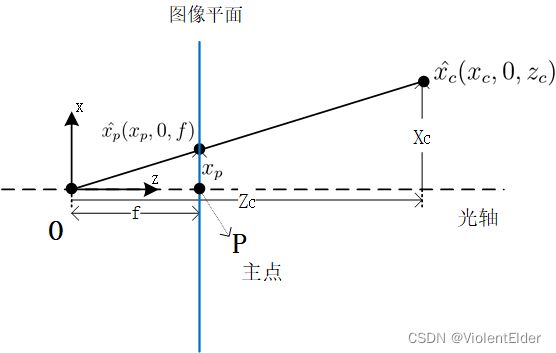
这里的$x_p=x^{{}^{\prime }}$，小孔成像的公式就变为了
$$\frac{x_p}{f}=\frac{x_c}{z_c}$$这样一来就消除了负号，同时像平面也变为了我们认知当中的正向图像。利用上述公式，我们在已知其中三个变量自然就可以求解剩下的未知量，但是这里存在一个问题，光轴并不是一根实际的线，而且相机系统的光心具体在什么位置是难以得到准确值的，这就意味着在以光心作为坐标系（这种坐标系称为相机坐标系）时，尽管已知物空间上一点，我们也很难量测其在这个坐标系下的具体位置$(x_c,y_c,z_c)$。因此我们需要以物空间中的一个具体位置来建立坐标系，而这个坐标系即世界坐标系。

除此之外我们还需要注意到，无论相机坐标系也好，还是世界坐标系也好，他们都是一个三维的坐标系，但是我们实际拍摄的图像只是二维的，也就是说经过小孔成像模型投影后得到的像点$x_p$我们实质只关心其前两个维度的变量$(x_p,y_p)$即可，因此可以直接在图像平面的主点（即图像的中心）上建立二维的$x-y$坐标系即可，而这个坐标系被称为图像坐标系。

当然，这三个坐标系的度量都是长度单位（一般采用mm），但我们实际拿到的数字图像单位是像素，而且数字图像在PC的存储是以矩阵的形式存储，矩阵的起始点位于左上角，因此我们要引入在数字图像上的计算还需要以图像左上角位置建立的，度量单位是像素的坐标系，而这个坐标系被称为像素坐标系。其与图像坐标系的差异如下图所示，$u-v$坐标系为像素坐标系，$X_p-Y_p$坐标系为图像坐标系，$(c_x,c_y)$表示主点$P$在像素坐标系下的位置。

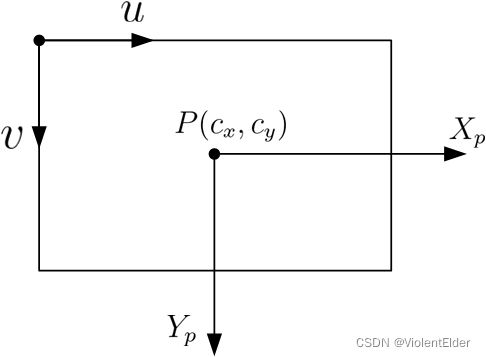
通过上面说到的四个坐标系的相互变换，我们即可构建数字图像上的某个像素与实际空间中的具体物点之间的映射关系了，而标定的目的就是去求解在这些坐标系相互变换中用到的各种未知量。

二.坐标系的变换

1.世界坐标系到相机坐标系的变换（刚体变换）[$\widehat{{\mathbf{x}}_{\mathbf{w}}}\to \widehat{{\mathbf{x}}_{\mathbf{c}}}$]

刚体变换(regidbody motion)：三维空间中， 当物体不发生形变时，对一个几何物体作旋转， 平移的运动，称之为刚体变换²。

由于世界坐标系和相机坐标系都是右手坐标系，两者之间的转换并不存在形变，仅通过刚体变换的方式即可进行相互的转换，设物空间中一点，在世界坐标系中的表达为$\widehat{{\mathbf{x}}_{\mathbf{w}}}=[x_w,y_w,z_w{]}^T$，在相机坐标系下的表达为$\widehat{{\mathbf{x}}_{\mathbf{c}}}=[x_c,y_c,z_c{]}^T$，根据刚体变换的数学表达，我们可以得到如下的转换关系：
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\left[\begin{array}{lll}{r}_{00}& r_{01}& r_{02}\\ r_{10}& r_{11}& r_{12}\\ r_{20}& r_{21}& r_{22}\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\end{array}\right]+\left[\begin{array}{c}{T}_x\\ T_y\\ T_z\end{array}\right]$$为了让计算更加规整，将这个线性表示写为齐次形式（后续的变换也都采用齐次坐标进行表达）：

齐次坐标：把n维空间上的点，用（n+1）维的向量进行表示。¹

$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{cc}R& t\\ 0_3^T& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$其中，$R$是$3\times 3$的正交单位矩阵【三个列向量两两正交，这个性质在后续标定算法中非常重要】被称为旋转矩阵；$t$为$3\times 1$的平移向量。由于这两者只与相机系统在世界坐标系中所处的位置有关，与系统本身的参数特性无关，因此，$R$和$t$被称为外参，$\left[\begin{array}{cc}R& t\\ 0_3^T& 1\end{array}\right]$被称为外参矩阵。

2.相机坐标系到图像坐标系的变换（射影变换，基于小孔成像模型）[$\widehat{{\mathbf{x}}_{\mathbf{c}}}\to \widehat{{\mathbf{x}}_{\mathbf{p}}}$]

利用上一章提到的小孔成像模型，设物空间中一点$\widehat{{\mathbf{x}}_{\mathbf{c}}}$经镜头系统投影到像面的位置为$\widehat{{\mathbf{x}}_{\mathbf{p}}}=[x_p,y_p,1{]}^T$【由于图像时二维的，此处做了降维】，我们可以建立从相机坐标系到图像坐标系射影变换的数学表达：
$$\left[\begin{array}{l}{x}_p\\ y_p\\ 1\end{array}\right]=\left[\begin{array}{llll}f/z_c& 0& 0& 0\\ 0& f/z_c& 0& 0\\ 0& 0& 1/z_c& 0\end{array}\right]\left[\begin{array}{c}{x}_c\\ y_c\\ z_c\\ 1\end{array}\right]$$将$z_c$提出来放到等式的左侧有：
$$z_c\left[\begin{array}{l}{x}_p\\ y_p\\ 1\end{array}\right]=\left[\begin{array}{llll}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}{x}_c\\ y_c\\ z_c\\ 1\end{array}\right]$$这里的$f$即相机系统的焦距，但它并不是简单的镜头规格书上写好的参数，这是由于镜头生产和加工是有偏差的，而且每当我们旋钮定焦镜头上的对焦环时，都会造成焦距的轻微变化，这也是为什么每次旋拧完镜头对焦环后都需要重新标定的缘故。注意到这一步为止，矩阵两边的单位依然是物理尺寸（如mm）。

3.图像坐标系到像素坐标系的变换（平移+单位缩放）[$\widehat{{\mathbf{x}}_{\mathbf{p}}}\to \widehat{{\mathbf{x}}_{\mathbf{s}}}$]

由于图像坐标系与像素坐标系的差异如下图所示：

要将图像坐标系$X_p-Y_p$下的表示转换为以左上角为原点的像素坐标系$u-v$的表示，需要进行坐标系的平移以及尺度单位的缩放。设图像坐标系圆心$P$（即主点）像素坐标系下的位置（单位：像素）为$(c_x,c_y)$【这个位置在理想模型中即画面的正中心，但实际由于相机Sensor安装时候的偏差，画面正中心的点未必与光轴重合，这导致主点坐标并不位于正中间，当然，越好的相机这两者之间会越接近】，单位尺寸内的像素数为$s_x、s_y$（即像元尺寸的倒数，单位：像素/mm）【存在两个方向主要是由于Sensor安装带来的像面与理想像面的差异 以及 像元在sensor上并不一定是密集排列的，其存在周边电路造成像元很难是一个标准的正方形】。这样一来我们可以得到如下的关系式：
$$\{\begin{array}{c}u=c_x+x_p\cdot s_x\\ v=c_y+y_p\cdot s_y\end{array}$$将其写为齐次坐标下的表达
$$\left[\begin{array}{l}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{lll}{s}_x& 0& c_x\\ 0& s_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_p\\ y_p\\ 1\end{array}\right]$$

4.总结

通过上面介绍的坐标系之间转换过程，我们可以将这三者联立相乘，写为一个整体有
$$\begin{array}{rl}{z}_c\left[\begin{array}{l}u\\ v\\ 1\end{array}\right]& =z_c\left[\begin{array}{ccc}{s}_x& 0& c_x\\ 0& s_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}{x}_p\\ y_p\\ 1\end{array}\right]=\left[\begin{array}{ccc}{s}_x& 0& c_x\\ 0& s_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}{x}_c\\ y_c\\ z_c\\ 1\end{array}\right]\\ & =\left[\begin{array}{ccc}{s}_x& 0& c_x\\ 0& s_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cccc}{r}_{00}& r_{01}& r_{02}& T_x\\ r_{10}& r_{11}& r_{12}& T_y\\ r_{20}& r_{21}& r_{22}& T_z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]\end{array}$$由于等式中前两个矩阵$\left[\begin{array}{ccc}{s}_x& 0& c_x\\ 0& s_y& c_y\\ 0& 0& 1\end{array}\right]，\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]$中的参数只和相机系统本身的参数性质有关，因此可以将其相乘得到一个新的矩阵，设组合量$f\cdot s_x=f_x，f\cdot s_y=f_y$，则上式可以被写为
$$z_c\left[\begin{array}{l}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cc}R& t\\ 0_3^T& 1\end{array}\right]\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right]$$其中$\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$被称为内参矩阵（Intrinsic Matrix），$f_x、f_y、c_x、c_y$就是内参（Intrinsic Parameters）；$\left[\begin{array}{cc}R& t\\ 0_3^T& 1\end{array}\right]$被称为外参矩阵（Extrinsic Matrix），$R$和$t$被称为外参（Extrinsic Parameters）。希望通过这一部分的总结，可以方便读者之后能很快速的解读MATLAB或者OpenCV对相机标定后的结果。

在部分教材和帖子中，会将两个组合量$f_x，f_y$说成是相机系统沿$x/y$的焦距，但我认为这种说法是存在歧义的【一个光学专业学生的较真 】，因此对于MATLAB或者OpenCV输出内参矩阵中的$f_x，f_y$（单位：像素），请不要直接与你采用的镜头焦距（单位：mm）作对比，你需要将$f_x，f_y$乘以所采用相机Sensor的像元尺寸（单位：um/像素）后再进行比对。

利用刚刚得到的公式，在通过标定确定相机系统的内参和外参之后，我们便可以计算物空间上任意一点$(x_w,y_w,z_w)$投影到相机画面上的像素坐标$(u,v)$【$z_c$可以通过$\widehat{{\mathbf{x}}_{\mathbf{w}}}\to \widehat{{\mathbf{x}}_{\mathbf{c}}}$】得到。但是，反过来通过图像上一点$(u,v)$，在相机系统的内参和外参已知的情况下，是无法还原物空间上的精确一点$(x_w,y_w,z_w)$的！！，这是因为$z_c$此时是未知量，只有确定$z_c$，即已知被摄面到相机系统的物距或者被摄面相对于世界坐标系的位置时，才能还原物空间的精确一点。

这也从数学的角度上说明了，采用单个常规相机，在没有其他辅助手段以及相机固定（外参固定）的情况下，是无法实现三维重建的原因，而且即使要实现准确的二维测量，也需要被摄面到相机的距离已知且固定【工厂采用视觉技术的自动化设备，一旦摄像机机位发生变化，都是需要重新标定的，并且考虑到被摄面到相机的距离不方便测量，标定时会故意将世界坐标系建立在被摄面上（这种场景下的标定需要将标定板厚度考虑进来）】

三.畸变模型

从理想情况上来说，在上面的内参和外参结果知道后就可以构建图像与实际被摄物的映射关系了，但实际的相机系统并不是理想的模型，由于镜头本身特性的缘故，以及相机和镜头生产过程中受制造精度和组装工艺带来的偏差，造成得到的图像会存在失真，而这些失真中对刚才的投影公式影响最大的就是——畸变。

在计算机视觉的相机模型中，畸变主要分为径向畸变（由镜头本身特性以及制造精度决定）和切向畸变（由相机和镜头的组装工艺带来的偏差决定）。

这里需要纠正一下 大奥特曼打小怪兽 博主描述的 “透镜的畸变主要分为径向畸变和切向畸变”，镜头本身特性带来的畸变只会影响径向畸变，所以切向畸变并不能说是透镜的畸变。【一个光学专业学生对自己镜头设计知识的自信！ 】

1.径向畸变

径向畸变是沿着透镜半径方向分布的畸变，由镜头本身特性以及制造精度决定，主要影响因素还是镜头本身的特性（镜头的5种单色像差之一就是畸变），其中视场是径向畸变重要影响因素，一个镜头其视场角越大，其视场边缘的畸变也就越大，当然廉价的镜头由于对于镜头设计优化和工装的要求较低，其畸变也会很大。这也是为什么大多数高精度的视觉测量系统会采用中长焦镜头（焦距越长视场越小）的原因了。

折射理论中折射角和入射角的关系是非线性的，只有在近轴区域才可以看做是线性关系（理想成像），远离画面中心的位置这种非线性差异就会越大（非理想成像），此时像差也会越大【有关镜头相关的知识今后有空我也做个汇总好了】

径向畸变主要包括桶形畸变和枕形畸变两种。以下分别是枕形和桶形畸变示意图：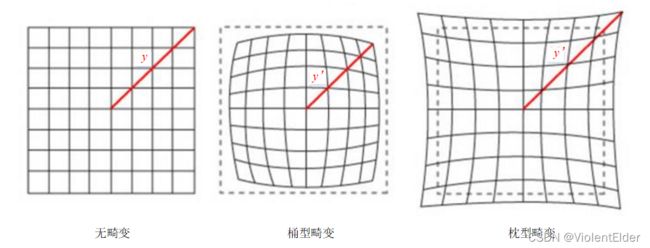
两种畸变的实际效果如下：

2.切向畸变

切向畸变是由于感光面（Sensor面）与光轴不垂直所产生的一种畸变，这种畸变由相机和镜头的组装工艺带来的偏差决定（相机安装的偏差带来实际感光面与理想像面的不平行，镜头安装的偏差导致实际光轴与理想光轴的不重合），这种偏差的示意图如下图所示³：

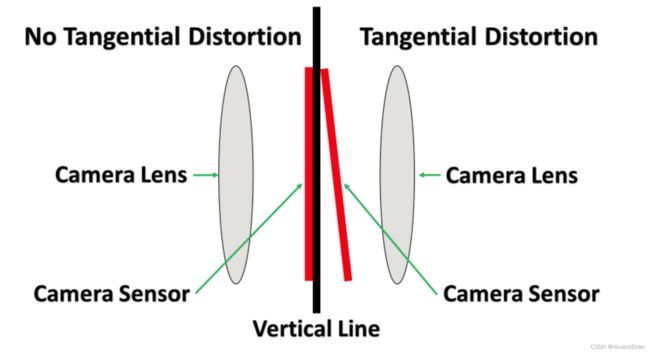
3.数学模型

上述两种畸变反应在图像上就是图像边缘的像素点相对于理想模型下的像素点会有位置的偏移，导致投影公式计算得到的不够准确。同时由于两种畸变无一例外都是图像中心畸变很小，但是越往外畸变越大，因此畸变的数学模型可以建立在以主点为原点的图像坐标系上，如下图所示：

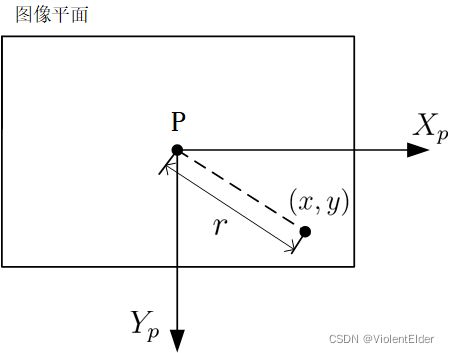
其中$(x,y)$表示在理想图像平面下的像素点坐标，$r$表示理想像素点距离图像中心（即主点$P$）的距离。设经过畸变之后，在实际图像平面上对应的点为$(x_{dist},y_{dist})$，则可以有如下的关系式：
$$\{\begin{array}{c}{x}_{dist}=x\left(1+k_1{r}^2+k_2{r}^4+k_3{r}^6\right)+2p_{1}xy+p_2\left(r^2+2x^2\right)\\ y_{dist}=y\left(1+k_1{r}^2+k_2{r}^4+k_3{r}^6\right)+p_2\left(r^2+2y^2\right)+2p_{2}xy\end{array}$$其中$k_1，k_2，k_3$用于描述径向畸变，是对主点周围进行泰勒级数展开后的前3项，当$k>0$时，距离主点越远的点受畸变影响其向外偏离的程度就越大，此时为枕形畸变（正畸变）；反之，当$k<0$时，距离主点越远的点受畸变影响其向内偏离的程度就越大，此时为桶形畸变（负畸变）。

理论上来说，径向畸变的描述可以无限展开，但是意义不大，一般的系统进行图像矫正采用前两项即可，大畸变系统会需要第三项也参与计算

$p_1，p_2$用于描述切向畸变，其具体的由来可以参考“铅锤”模型，详见⁴。这5个参数由于都是相机系统内部特性带来的参数，故也算是相机内参的一部分。

注：在Opencv中他们被排列成一个5×1的矩阵，依次包含$k_1，k_2，p_1，p_2，k_3$，利用这5个参数即可校正由于畸变导致的图像形变失真。

四.总结

通过上面的推导，我们可以总结一下，要实现从物空间任意一点到相机图像的投影我们需要计算得到哪些参数：

• 内参：$f_x，f_y$（焦距与$X/Y$方向的像元尺寸倒数的乘积），$c_x、c_y$（主点在像素坐标系下的坐标位置），$k_1，k_2，k_3$（描述径向畸变的参数），$p_1，p_2$（描述切向畸变的参数）

• 外参：$R$（3x3旋转矩阵），$t$（3x1平移向量）

利用相机标定的算法，我们可以求解出这些参数，从而可以实现从像到物或从物到像的相互映射。

五.写在最后

其实现在关于相机标定有非常多的资料，但我还是啰啰嗦嗦的写了这篇帖子，主要还是想要把这一块知识能理得更顺，将很多参考资料中省略掉的那些过渡进行一个补充，希望能方便更多和我一样的初学者能从中将这知识吃的更透彻，而不是只见山之一貌，海之一角，片面的看待问题。里面很多过渡属于是我自己的推导，如果有片面或者不够准确的地方，希望该领域的大佬们能帮忙提点出来，确保知识输出的准确与客观。

参考引用

---

1. 凯勒, 布拉德斯基, 刘昌祥, 吴雨培, and 王成龙. 学习OpenCV 3 中文版. 北京: 清华大学出版社, 2018. ↩︎ ↩︎

2. 第六节、双目视觉之相机标定 ↩︎ ↩︎

3. Chiou G N. Reducing the Variance of Intrinsic Camera Calibration Results in the ROS Camera_Calibration Package[J]. Masters Thesis, 2017: 9. ↩︎

4. Brown D C. Decentering distortion of lenses[J]. Photogrammetric Engineering and Remote Sensing, 1966. ↩︎