【CS224n】2斯坦福大学深度学习自然语言处理课程笔记——词向量、词义和神经分类器
Natural Language Processing with Deep Learning 课程笔记2
- 1. 词向量和word2vec
- 2. 优化基础知识
- 3. 我们能否通过计数更有效地抓住词义的本质?
- 4. 词向量的GloVe模型
- 5. 评价词向量
- 6. 词义
- 7. 回顾分类和神经网络的不同之处
- 8. 介绍神经网络
- 小结
主要目标:在课后能读懂word embeddings论文
1. 词向量和word2vec
回忆:word2vec的主要思想
- 从随机词向量开始
- 遍历整个语料库中的每一个单词
- 尝试使用单词向量 P ( o ∣ c ) = exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) P(o \mid c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} P(o∣c)=∑w∈Vexp(uwTvc)exp(uoTvc)预测周围的单词
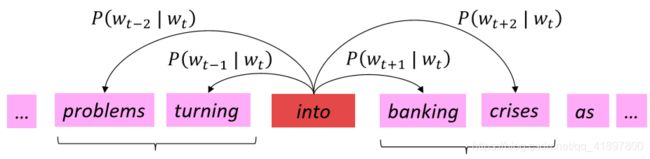
- 学习:更新向量,以便它们能更好地预测周围的实际词汇
- 做的不多,这个算法学习单词向量,可以很好地捕捉单词空间中的单词相似度和有意义的方向!
Word2vec参数和计算
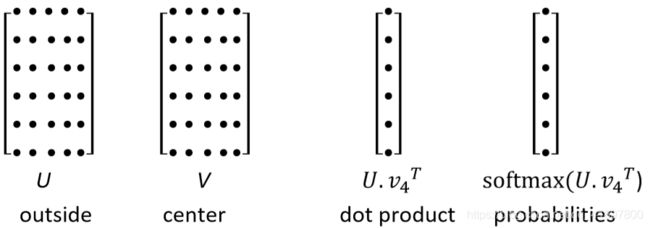
n × d ⋅ d → 1 → n × 1 → softmax n × 1 n \times d \cdot d \rightarrow 1 \rightarrow n \times 1 \stackrel{\text { softmax }}{\rightarrow} n \times 1 n×d⋅d→1→n×1→ softmax n×1
- 每行代表一个单词的词向量,点乘后得到的分数通过softmax映射为概率分布,并且我们得到的概率分布是对于该中心词而言的上下文中单词的概率分布,该分布于上下文所在的具体位置无关,所以在每个位置的预测都是一样的
- 该模型在每个位置都做出了相同的预测(词袋模型)。我们希望有一个模型,能给所有在上下文中出现的词提供一个合理的高概率估计(根本不经常出现)
Word2vec通过将相似的词放在附近的空间来最大化目标函数
2. 优化基础知识
详见上一篇:【CS224n】1斯坦福大学深度学习自然语言处理课程笔记
随机梯度与词向量!
- 在每个这样的窗口迭代地采取SGD
- 但在每个窗口中,我们最多只有2m+1个字,所以 ∇ θ J ( θ ) \nabla_{\theta} J(\theta) ∇θJ(θ)是非常稀少的
∇ θ J t ( θ ) = [ 0 ⋮ ∇ v l i k e ⋮ 0 ∇ u I ⋮ ∇ u l e a r n i n g ⋮ ] ∈ R 2 d V \nabla_{\theta} J_{t}(\theta)=\left[\begin{array}{l}0 \\ \vdots \\ \nabla_{v_{l i k e}} \\ \vdots \\ 0 \\ \nabla_{u_{I}} \\ \vdots \\ \nabla_{u_{l e a r n i n g}} \\ \vdots\end{array}\right] \in \mathbb{R}^{2 d V} ∇θJt(θ)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡0⋮∇vlike⋮0∇uI⋮∇ulearning⋮⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤∈R2dV - 我们可能只更新实际出现的词向量!
- 解决方案:要么你需要进行稀疏矩阵更新操作,只更新全嵌入矩阵U和V的某些行(在实际的DL包中,行不是列!),要么你需要保留字向量的哈希值

- 如果你有数以百万计的单词向量,并且做分布式计算,重要的是不必到处发送巨大的更新!
负采样的skip-gram(跳格)模型(HW2)
- 归一化项的计算成本很高
- P ( o ∣ c ) = exp ( u o T v c ) ∑ w ∈ V exp ( u w T v c ) P(o \mid c)=\frac{\exp \left(u_{o}^{T} v_{c}\right)}{\sum_{w \in V} \exp \left(u_{w}^{T} v_{c}\right)} P(o∣c)=∑w∈Vexp(uwTvc)exp(uoTvc)
- 因此,在标准的word2vec和HW2中,你实现了负采样的skip-gram模型
- 主要思路:对一个真对(中心词及其上下文窗口中的一个词)与几个噪声对(中心词与随机词配对)进行二元逻辑回归训练
“Distributed Representations of Words and Phrases and their Compositionality” (Mikolovet al. 2013)
-
总体目标函数(他们最大化)
J t ( θ ) = log σ ( u o T v c ) + ∑ i = 1 k E j ∼ P ( w ) [ log σ ( − u j T v c ) ] J_{t}(\theta)=\log \sigma\left(u_{o}^{T} v_{c}\right)+\sum_{i=1}^{k} \mathbb{E}_{j \sim P(w)}\left[\log \sigma\left(-u_{j}^{T} v_{c}\right)\right] Jt(θ)=logσ(uoTvc)+i=1∑kEj∼P(w)[logσ(−ujTvc)]
J ( θ ) = 1 T ∑ t = 1 T J t ( θ ) J(\theta)=\frac{1}{T} \sum_{t=1}^{T} J_{t}(\theta) J(θ)=T1t=1∑TJt(θ) -
Logistic/sigmoid函数: σ ( x ) = 1 1 + e − x \sigma(x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
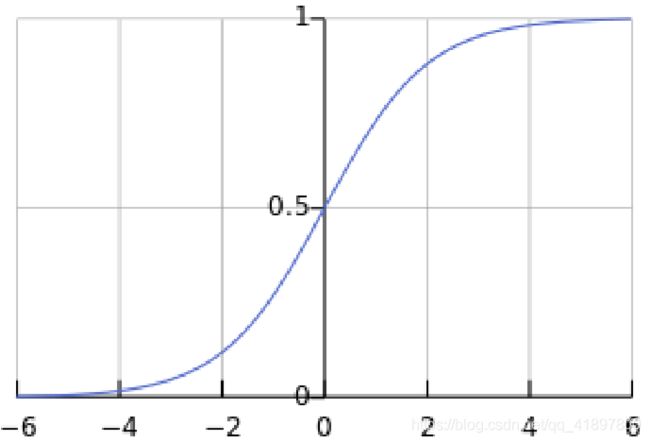
-
我们最大限度地提高两个词在第一对数中共同出现的概率,并使噪声词的概率最小化
-
符号更类似于toclass和HW2:
J neg-sample ( u o , v c , U ) = − log σ ( u o T v c ) − ∑ k ∈ { K sampled indices } log σ ( − u k T v c ) J_{\text {neg-sample }}\left(\boldsymbol{u}_{o}, \boldsymbol{v}_{c}, U\right)=-\log \sigma\left(\boldsymbol{u}_{o}^{T} \boldsymbol{v}_{c}\right)-\sum_{k \in\{K \text { sampled indices }\}} \log \sigma\left(-\boldsymbol{u}_{k}^{T} \boldsymbol{v}_{c}\right) Jneg-sample (uo,vc,U)=−logσ(uoTvc)−k∈{K sampled indices }∑logσ(−ukTvc) -
我们取k个负样本(用词概率)
-
最大限度地提高真实外字出现的概率,最大限度地降低中心字周围随机字出现的概率
-
取样, P ( w ) = U ( w ) 3 / 4 / Z \mathrm{P}(w)=\mathrm{U}(w)^{3 / 4} / Z P(w)=U(w)3/4/Z,单字分布U(w)提高到3/4次方(我们在入门代码中提供了这个函数)
U ( w ) \mathrm{U}(w) U(w)是 unigram 分布通过3/4次方,相对减少常见单词的频率,增大稀有词的概率。 Z Z Z用于生成概率分布 -
Power使频率较低的词被抽查的频率更高
3. 我们能否通过计数更有效地抓住词义的本质?
为什么不直接抓取共现次数?
构建共现矩阵X
- 2个选项:窗口与完整文档
- 窗口:类似于word2vec,在每个词周围使用窗口捕捉一些语法和语义信息
- 词-文共现矩阵将给出一般主题(所有的体育术语将有相似的条目),从而进行 “潜在语义分析”
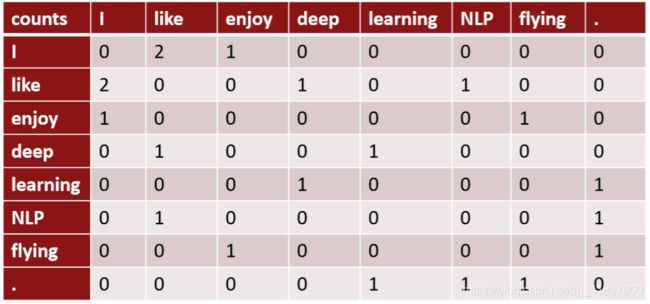
例子:基于窗口的共同出现矩阵
共现向量
- 简单的计数共现向量
矢量随着词汇量的增加而增大
非常高的维度:需要大量的存储空间(虽然稀少)
后续分类模型存在稀疏性问题→模型的鲁棒性较差 - 低维向量
理念:将 "大部分 "重要信息存储在一个固定的、数量不多的维度中:密集向量
通常为25-1000个维度,类似于word2vec
如何降低维度?
经典方法:X上的尺寸缩小法(HW1)
共同发生矩阵X的奇异值分解
使用SVD方法将X分解成 U Σ V ⊤ U \Sigma V^{\top} UΣV⊤,其中U和V是正交的
Σ \Sigma Σ是对角线矩阵,对角线上的值是矩阵的奇异值,U、V是对应于行和列的正交基
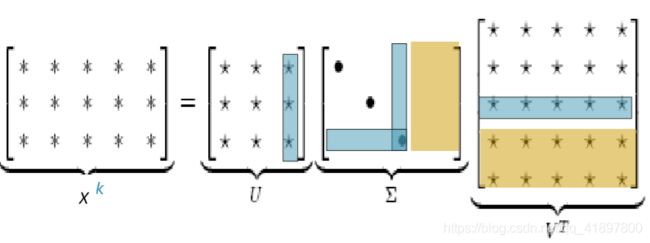
只保留k个奇异值,以便归纳
X ^ \hat{X} X^ 是X的最佳秩k近似,用最小二乘法表示
经典的线性代数结果。对于大矩阵来说,计算成本很高
Hacks to X(Rohde等人2005年在COALS中使用的几种方法)
按比例调整 counts 会很有效
- 在原始计数上运行SVD效果不佳
- 缩放cells中的计数,可以帮助很多
问题:问题:功能词(the、he、has)过于频繁的语法影响太大。进行了一些修正
频数对数
min(X,t),t ≈100
忽略功能词 - 坡道窗,算近的词比算远的词要多一些
- 用皮尔逊相关性代替计数,然后将负值设置为0
- 等等
缩放向量中出现了有趣的语义模式
4. 词向量的GloVe模型
| 基于计数 | 直接预测 |
|---|---|
| LSA, HAL (Lund & Burgess) | Skip-gram/CBOW (Mikolovet al) |
| COALS, Hellinger-PCA (Rohde et al, Lebret& Collobert) | NNLM, HLBL, RNN (Bengioet al; Collobert& Weston; Huang et al; Mnih & Hinton) |
| 训练速度快 | 随语料库大小而伸缩 |
| 高效使用统计数据 | 统计资料的使用效率低下 |
| 主要用于捕捉词的相似性 | 提高其他任务的性能 |
| 对大数的重视程度不成比例 | 可以捕捉到超越词语相似性的复杂模式 |
在向量差异中编码意义成分
矢量差异的编码意义
将两个流派的想法结合起来,在神经网络中使用计数矩阵
[Pennington, Socher, and Manning, EMNLP 2014]
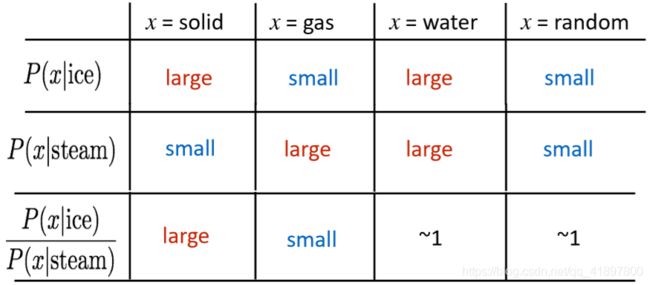
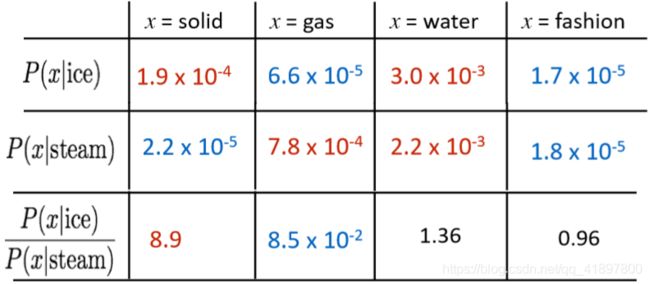
关键性见解:共现概率的比率可以对meaning component进行编码
例如我们想区分热力学上两种不同状态ice冰与蒸汽steam,它们之间的关系可通过与不同的单词 x 的co-occurrence probability 的比值来描述,所以相较于单纯的co-occurrence probability,实际上co-occurrence probability的相对比值更有意义
问:在词向量空间中,我们如何捕捉共现概率的比率作为线性意义分量?
答:对数双线性模型: w i ⋅ w j = log P ( i ∣ j ) w_{i} \cdot w_{j}=\log P(i \mid j) wi⋅wj=logP(i∣j)
with vector differences(有向量差的): w x ⋅ ( w a − w b ) = log P ( x ∣ a ) P ( x ∣ b ) w_{x} \cdot\left(w_{a}-w_{b}\right)=\log \frac{P(x \mid a)}{P(x \mid b)} wx⋅(wa−wb)=logP(x∣b)P(x∣a)
如果使向量点积等于共现概率的对数,那么向量差异变成了共现概率的比率
结合了两个的优点——GloVe
[Pennington, Socher, and Manning, EMNLP 2014]
w i ⋅ w j = log P ( i ∣ j ) w_{i} \cdot w_{j}=\log P(i \mid j) wi⋅wj=logP(i∣j)
J = ∑ i , j = 1 V f ( X i j ) ( w i T w ~ j + b i + b ~ j − log X i j ) 2 J=\sum_{i, j=1}^{V} f\left(X_{i j}\right)\left(w_{i}^{T} \tilde{w}_{j}+b_{i}+\tilde{b}_{j}-\log X_{i j}\right)^{2} J=i,j=1∑Vf(Xij)(wiTw~j+bi+b~j−logXij)2
GloVe结果
与frog(青蛙)最接近的词
1.frogs(青蛙)
2.toad (蟾蜍)
3.litoria (利托里亚)
4.leptodactylidae(细足亚科)
5.rana (林蛙)
6.lizard (蜥蜴)
7.eleutherodactylus(指甲虫)

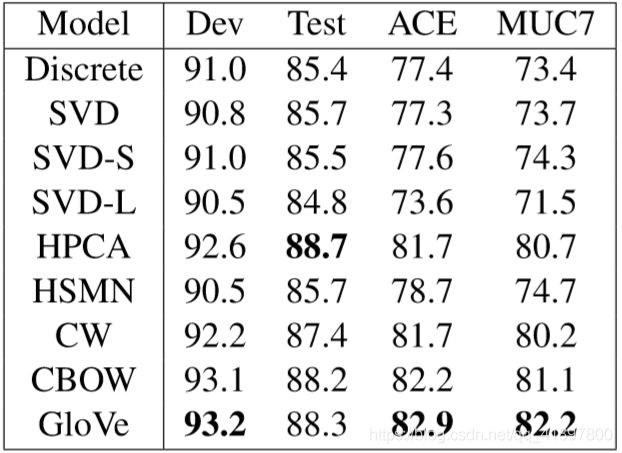
5. 评价词向量
与NLP中的一般评价相关:内在与外在的评价
| 内在 | 外在 |
|---|---|
| 对某一具体/中间子任务的评价 | 对实际任务的评价 |
| 计算速度快 | 可能需要很长的时间来计算精度 |
| 有助于了解该系统 | 不清楚是子系统出了问题,还是子系统之间的互动或其他子系统出了问题 |
| 不清楚是否真的有用,除非建立与实际任务的关联性 | 如果用一个子系统替换另一个子系统来提高精度→Winning! |
本质词向量评价
-
词向量类比
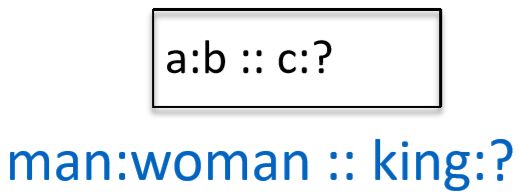
d = arg max i ( x b − x a + x c ) T x i ∥ x b − x a + x c ∥ d=\arg \max _{i} \frac{\left(x_{b}-x_{a}+x_{c}\right)^{T} x_{i}}{\left\|x_{b}-x_{a}+x_{c}\right\|} d=argimax∥xb−xa+xc∥(xb−xa+xc)Txi

-
通过其加法后的余弦距离对直观语义和句法类比问题的捕捉程度来评价词向量的好坏
-
抛弃搜索中的输入词!
-
问题:如果信息有但不是线性的怎么办?
Glove可视化

Glove可视化: 公司 - CEO
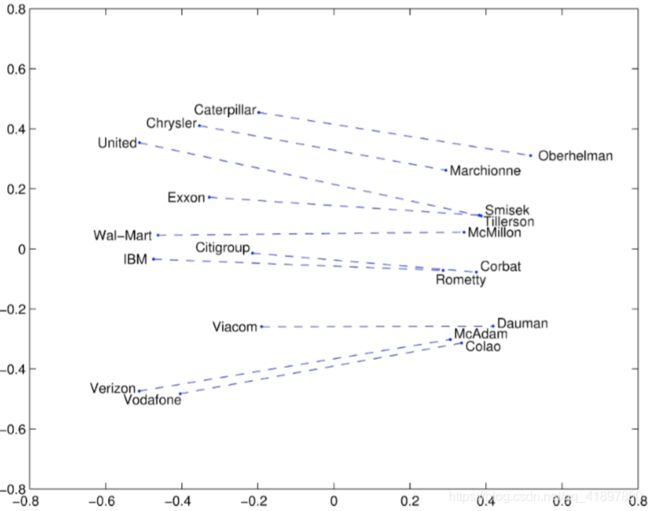
Glove可视化: 比较级和最高级

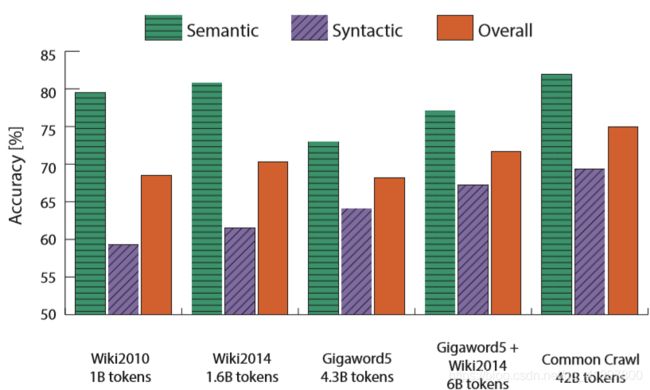
类比评估和超参数
- Glove论文中的一些观点也已经被证明可以改善跳格(SG)模型
外在词向量评价
- 词向量的外在评价。这一类的所有后续NLP任务,很快会有更多的例子
- 一个好的词向量可以直接帮助的例子:命名实体识别:识别对个人、组织或地点的引用
6. 词义
词义和词义歧义
- 大多数词语都有很多含义!
特别是常见的词语
特别是存在已久的词语 - 例子:pike
A type of elongated fish 梭子鱼;狗鱼;
A sharp point or staff 长矛;
A type of road (英格兰北部的)山峰,陡峰,
To kill or pierce with a pike 用矛刺穿
A railroad line or system
The future (coming down the pike)
A type of body position (as in diving)
To make one’s way (pike along)
In Australian English, pike means to pull out from doing something: I reckon he could have climbed that cliff, but he piked! - 是一个向量就能涵盖所有这些含义,还是我们有一个乱七八糟的东西?
通过全局上下文和多词原型来改进词的表示方法
Huang et al. 2012
思想:围绕着单词进行集群,每个单词都被分配到多个不同的集群 b a n k 1 \mathrm{bank}_{1} bank1, b a n k 2 \mathrm{bank}_{2} bank2等,进行再训练

词义的线性代数结构,与多义词的应用
Arora, …, Ma, …, TACL 2018
- 一个词的不同意义存在于一个线性叠加(加权和)的标准词嵌入中,如word2vec
- v pike = α 1 v pike 1 + α 2 v pike 2 + α 3 v pike 3 v_{\text {pike }}=\alpha_{1} v_{\text {pike }_{1}}+\alpha_{2} v_{\text {pike }_{2}}+\alpha_{3} v_{\text {pike }_{3}} vpike =α1vpike 1+α2vpike 2+α3vpike 3
- 其中 α 1 = f 1 f 1 + f 2 + f 3 \alpha_{1}=\frac{f_{1}}{f_{1}+f_{2}+f_{3}} α1=f1+f2+f3f1等,为频率 f f f,只是加权平均值就已经可以获得很好的效果
- 令人惊讶的结果:因为有了稀疏编码的概念,你实际上可以将感官分离出来(只要它们是相对常见的)!
- 可以理解为由于单词存在于高维的向量空间之中,不同的纬度所包含的含义是不同的,所以加权平均值并不会损害单词在不同含义所属的纬度上存储的信息
7. 回顾分类和神经网络的不同之处
- 一般来说,我们的训练数据集由以下样本组成:
{ x i , y i } i = 1 N \left\{x_{i}, y_{i}\right\}_{i=1}^{N} {xi,yi}i=1N - x i x_i xi是输入,例如,单词(索引或向量!)、句子、文档等
维度d - y i y_i yi是我们试图预测的标签(类之一),例如:
类:情绪(+/-)、命名实体、买卖决策
其他词
之后:多词序列
分类直觉
-
训练集: { x i , y i } i = 1 N \left\{x_{i}, y_{i}\right\}_{i=1}^{N} {xi,yi}i=1N
-
简单示例:
固定二维字向量输入分类
使用softmax/逻辑回归
线性决策边界 -
传统ML/统计方法:假设 x i x_i xi是固定的,训练(即设置)softmax/logistic回归权重 W ∈ R C × d W \in \mathbb{R}^{C \times d} W∈RC×d来确定如图所示的判定边界(超平面)

方法:对于每个固定的x,预测:
p ( y ∣ x ) = exp ( W y ⋅ x ) ∑ c = 1 C exp ( W c ⋅ x ) p(y \mid x)=\frac{\exp \left(W_{y} \cdot x\right)}{\sum_{c=1}^{C} \exp \left(W_{c} \cdot x\right)} p(y∣x)=∑c=1Cexp(Wc⋅x)exp(Wy⋅x)
Softmax 分类器
同样,我们可以将预测函数分为三个步骤:
- 对于 W W W的每一行,用 x x x计算点积: W y ⋅ x = ∑ i = 1 d W y i x i = f y W_{y} \cdot x=\sum_{i=1}^{d} W_{y i} x_{i}=f_{y} Wy⋅x=∑i=1dWyixi=fy
- 应用softmax函数求归一化概率
p ( y ∣ x ) = exp ( f y ) ∑ c = 1 C exp ( f c ) = softmax ( f y ) p(y \mid x)=\frac{\exp \left(f_{y}\right)}{\sum_{c=1}^{C} \exp \left(f_{c}\right)}=\operatorname{softmax}\left(f_{y}\right) p(y∣x)=∑c=1Cexp(fc)exp(fy)=softmax(fy) - 选择概率最大的 y y y
对于每个训练示例 ( x , y ) (x,y) (x,y),我们的目标是最大化正确类的概率,或者我们可以最小化该类的负对数概率:
− log p ( y ∣ x ) = − log ( exp ( f y ) ∑ c = 1 C exp ( f c ) ) -\log p(y \mid x)=-\log \left(\frac{\exp \left(f_{y}\right)}{\sum_{c=1}^{C} \exp \left(f_{c}\right)}\right) −logp(y∣x)=−log(∑c=1Cexp(fc)exp(fy))
cross entropy loss 交叉熵损失”训练
- 交叉熵的概念来源于信息论
- 设真概率分布为p
- 我们计算的模型概率为q
- 交叉熵为: H ( p , q ) = − ∑ c = 1 C p ( c ) log q ( c ) H(p, q)=-\sum_{c=1}^{C} p(c) \log q(c) H(p,q)=−∑c=1Cp(c)logq(c)
- 假设基本真值(或真值、黄金或目标)概率分布在正确的类别为1,在其他任何地方为0:p=[0,…,0,1,0,…,0],那么:由于有 one-hot p,唯一剩下的项是真类的负对数概率: − log p ( y i ∣ x i ) -\log p\left(y_{i} \mid x_{i}\right) −logp(yi∣xi)
对完整数据集进行分类
全数据集 { x i , y i } i = 1 N \left\{x_{i}, y_{i}\right\}_{i=1}^{N} {xi,yi}i=1N上的交叉熵损失函数:
J ( θ ) = 1 N ∑ i = 1 N − log ( e f y i ∑ c = 1 C e f c ) J(\theta)=\frac{1}{N} \sum_{i=1}^{N}-\log \left(\frac{e^{f_{y_{i}}}}{\sum_{c=1}^{C} e^{f_{c}}}\right) J(θ)=N1i=1∑N−log(∑c=1Cefcefyi)
而不是:
f y = f y ( x ) = W y ⋅ x = ∑ j = 1 d W y j x j f_{y}=f_{y}(x)=W_{y} \cdot x=\sum_{j=1}^{d} W_{y j} x_{j} fy=fy(x)=Wy⋅x=j=1∑dWyjxj
我们将用矩阵表示法写出f:
f = W x f=Wx f=Wx
传统ML优化
对于统计机器学习,通常只包含 W W W的元素:
θ = [ W ⋅ 1 ⋮ W ⋅ d ] = W ( : ) ∈ R C d \theta=\left[\begin{array}{l}W_{\cdot 1} \\ \vdots \\ W_{\cdot d}\end{array}\right]=W(:) \in \mathbb{R}^{C d} θ=⎣⎢⎡W⋅1⋮W⋅d⎦⎥⎤=W(:)∈RCd
因此,我们仅通过更新 W W W来更新决策边界:
∇ θ J ( θ ) = [ ∇ W ⋅ 1 ⋮ ∇ W ⋅ d ] ∈ R C d \nabla_{\theta} J(\theta)=\left[\begin{array}{l}\nabla_{W_{\cdot 1}} \\ \vdots \\ \nabla_{W \cdot d}\end{array}\right] \in \mathbb{R}^{C d} ∇θJ(θ)=⎣⎢⎡∇W⋅1⋮∇W⋅d⎦⎥⎤∈RCd
8. 介绍神经网络
神经网络分类器的胜利!
- 单凭Softmax(≈logistic回归)并不是很有效
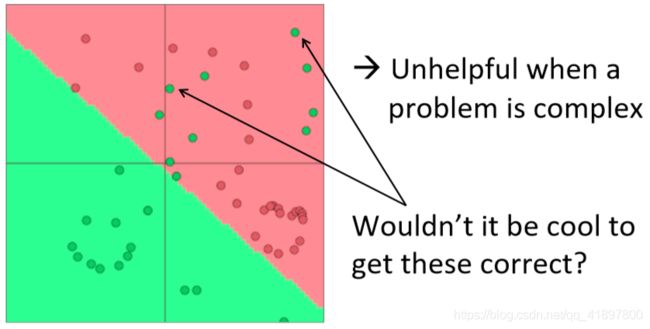
- Softmax classifier只给出线性决策边界
这可能是相当有限的
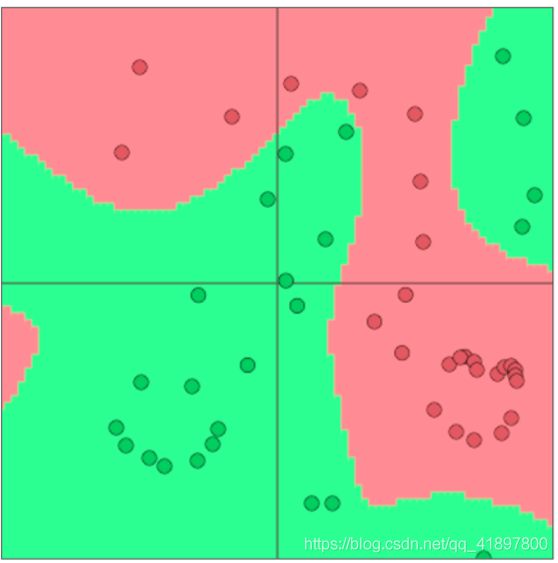
- 神经网络可以学习更复杂的非线性决策边界函数!
词向量分类差异#1
NLP深度学习中通常:
- 我们学习 W W W和单词向量 x x x
- 我们学习传统参数和(分布式!)表示
- 单词向量重新表示one-hot向量,它们在中间层向量空间中移动它们,以便于使用(线性)softmax分类器进行分类,概念上通过嵌入层:x=Le
∇ θ J ( θ ) = [ ∇ W ⋅ 1 ⋮ ∇ W ⋅ d ∇ x a a r d v a r k ⋮ ∇ x z e b r a ] ∈ R C d + V d \nabla_{\theta} J(\theta)=\left[\begin{array}{l}\nabla_{W \cdot 1} \\ \vdots \\ \nabla_{W \cdot d} \\ \nabla_{x_{a a r d v a r k}} \\ \vdots \\ \nabla_{x_{z e b r a}}\end{array}\right] \in \mathbb{R}^{C d+V d} ∇θJ(θ)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡∇W⋅1⋮∇W⋅d∇xaardvark⋮∇xzebra⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤∈RCd+Vd
V d Vd Vd参数非常多!
神经计算
神经元可以建模为二元逻辑回归单元
f f f=非线性激活函数(如sigmoid函数), w w w=权重, b b b=偏差, h h h=隐藏, x x x=输入
h w , b ( x ) = f ( w ⊤ x + b ) f ( z ) = 1 1 + e − z \begin{array}{l} h_{w, b}(x)=f\left(w^{\top} x+b\right) \\ f(z)=\frac{1}{1+e^{-z}} \end{array} hw,b(x)=f(w⊤x+b)f(z)=1+e−z1
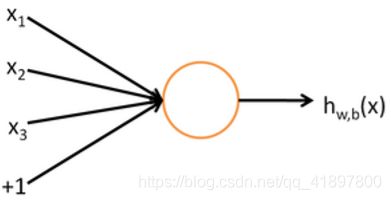

b: 我们可以有一个 "总是在 "的偏置特征,它给出了一个类的先决条件,或者把它分开,作为一个偏置项
w、b是这个神经元的参数,即这个逻辑回归模型的参数
区别二:神经网络=同时运行多个逻辑回归
如果我们把一个输入的向量通过一堆逻辑回归函数输入,那么我们就会得到一个输出的向量…。

但我们不必提前决定这些逻辑回归要预测的变量是什么!
…我们可以将其输入到另一个逻辑回归函数中

它是损失函数,会指导中间隐藏变量应该是什么,所以要做好下一层的目标预测等工作
在我们知道之前,我们已经有了一个多层神经网络…
-
我们有:
a 1 = f ( W 11 x 1 + W 12 x 2 + W 13 x 3 + b 1 ) a 2 = f ( W 21 x 1 + W 22 x 2 + W 23 x 3 + b 2 ) \begin{array}{l} a_{1}=f\left(W_{11} x_{1}+W_{12} x_{2}+W_{13} x_{3}+b_{1}\right) \\ a_{2}=f\left(W_{21} x_{1}+W_{22} x_{2}+W_{23} x_{3}+b_{2}\right) \end{array} a1=f(W11x1+W12x2+W13x3+b1)a2=f(W21x1+W22x2+W23x3+b2)
等等 -
在矩阵符号中:
z = W x + b a = f ( z ) \begin{array}{l} z=W x+b \\ a=f(z) \end{array} z=Wx+ba=f(z) -
激活 f f f是按元素来应用的:
f ( [ z 1 , z 2 , z 3 ] ) = [ f ( z 1 ) , f ( z 2 ) , f ( z 3 ) ] f\left(\left[z_{1}, z_{2}, z_{3}\right]\right)=\left[f\left(z_{1}\right), f\left(z_{2}\right), f\left(z_{3}\right)\right] f([z1,z2,z3])=[f(z1),f(z2),f(z3)]
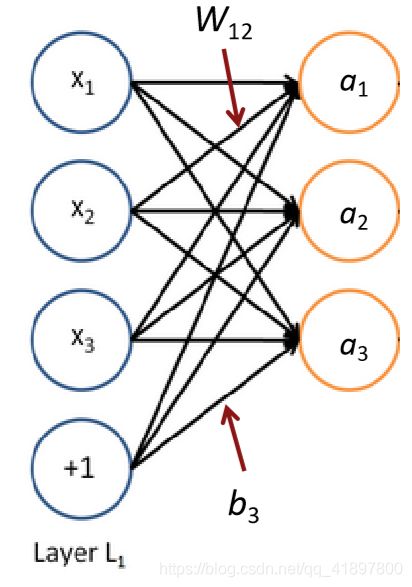
非线性(也就是 “f”)为什么需要非线性
例如:函数逼近,如回归或分类
- 如果没有非线性,深度神经网络除了线性变换之外,什么都做不了。
- 额外的层可以被编译成一个单一的线性变换。W1 W2 x= Wx
- 随着层数的增加,它们可以近似于更复杂的函数!
小结
回忆word2vec模型,计算成本很高,采用负采样。不通过计数而是降低维度的方法,包括奇异值分解、按比例调整计数。介绍GloVe模型,结合两者优点,以及如何评价词向量、多语义、神经网络知识