误差反向传播算法笔记

复习一下基础。

一、机器学习模型的处理方法

（1） 数据预处理： 经过数据的预处理，如去除噪声等。比如在文本分类中，去除停用词等。
（2） 特征提取：从原始数据中提取一些有效的特征。比如在图像分类中，提取边缘、尺度不变特征变换（Scale Invariant Feature Transform, SIFT）
（3）特征转换：对特征进行一定的加工，比如降维和升维。降维包括特征抽取（Feature Extraction）和特征选择（Feature Selection）两种途径。常用的特征转换方法有主成分分析、线性判别分析等。
（4）预测： 机器学习的核心部分，学习一个函数并进行预测。
NOTE: 开发一个机器学习系统的主要工作量都消耗在了预处理、特征提取以及特征转换上。

二、深度学习

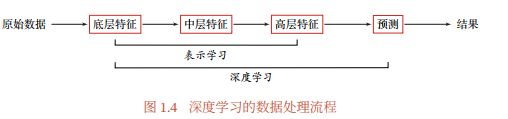
 深度学习是机器学习的一个子问题，其主要目的是从数据中自动学习到有效的特征表示。
经过多层的特征转换，把原始数据变成更高层次、更抽象的表示。这些学习到的表示可以替代人工设计的特征，从而避免“特征工程”。

深度学习是将原始的数据特征通过多步的特征转换得到的一种特征表示，并进一步输入到预测函数得到最终结果。和“浅层学习”不同，深度学习需要解决的关键问题是贡献度分配问题，即一个系统中不同的组件或其参数对最终系统输出结果的贡献或影响。
目前，深度学习采用的模型主要是神经网络模型，其主要原因是神经网络模型可以使用误差反向传播算法，从而可以比较好地解决贡献度分配问题。只要是超过一层的神经网络都会存在贡献度分配问题，因此可以将超过一层的神经网络都看做深度学习模型。

三、常用的神经网络结构

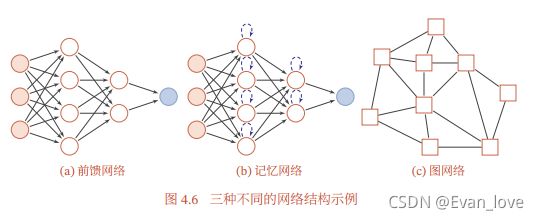
1、前馈网络（MLP）
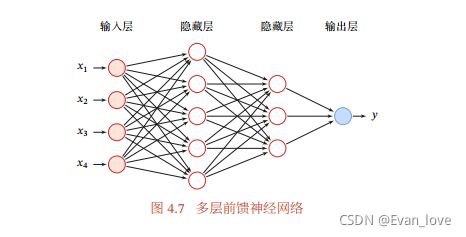
 前馈网络中各个神经元按接收信息的先后分为不同的组，每一组可以看做一个神经层。每一层中的神经元接收前一层神经元的输出，并输出到下一层神经元。整个网络的信息是朝着一个方向传播，没有反向传播，可以用一个有向无环图表示。（eg. 全连接前馈网络、CNN）。前馈网络可以看作一个函数，通过简单非线性函数的多次复合，实现输入空间到输出空间的复杂映射。这种网络结构简单，易于实现。
 在前馈神经网络中，各神经元分别属于不同的层。每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层。第0层称为输入层，最后一层称为输出层，其他中间层称为隐藏层。

2、记忆网络
也称为反馈网络，网络中的神经元不但可以接受其他神经元的信息，也可以接收自己的历史信息。和前馈网络相比，极意网络中的神经元具有记忆功能，在不同的时刻具有不同的状态。记忆网络中的信息传播可以是单向或双向传递，因此可用一个有向循环图或无向图来表示。（RNN、Hopfield网络、玻尔兹曼机、受限玻尔兹曼机等）。
3、图网络
图网络是定义在图结构数据上的神经网络，图中每个节点都由一个或一组神经元构成。节点之间的连接可以是有向的，也可以是无向的。每个节点可以收到来自相邻节点或者自身的信息。（知识图谱、社交网络、分子网络）。一些实现方式：图卷积网络、图注意力网络、消息传递神经网络等。

四、参数学习

如果采用交叉熵损失函数，对于样本（x,y)，其损失函数为：
$$\mathcal{L}(y,\hat{y})=-y^{T}log\hat{y}$$
其中$y\in \{0,1{\}}^C$为标签y对应的one-hot向量表示。
  给定训练集为$\mathcal{D}=\{(x^{(n)},y^{(n)}){\}}_{n=1}^N$,，将每个样本$x^{(n)}$输入给前馈神经网络，得到网络输出为${\hat{y}}^n$，其在数据集$\mathcal{D}$上的结构化风险函数为：
$$\mathcal{R}(W,b)=\frac{1}{N}\sum _{n=1}^N\mathcal{L}(y^{(n)},{\hat{y}}^{(n)})+\frac{1}{2}\lambda ||W|{|}_F^2$$
其中W和b分别表示网络中所有的权重矩阵和偏置向量；||W||_F^2是正则化项，用来防止过拟合；$\lambda >0$为超参数，$\lambda$越大，W越接近于0,。这里的$||W|{|}_F^2$一般使用Frobenius范数。
$$||W|{|}_F^2=\sum _{l=1}^L\sum _{i=1}^{M_l}\sum _{j=1}^{M_{i-1}}(w_{ij}^{(l)}{)}^2$$
有了学习准则和训练样本，网络参数可以用过梯度下降法来进行学习。在梯度下降方法的每次迭代中，第$l$层的参数$W^{(l)}$和$b^{(l)}$参数更新方式为：

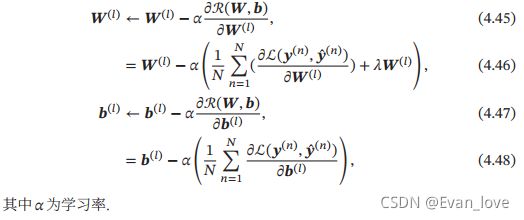
如果通过链式法则逐一对每个参数进行求偏导数比较低效。在神经网络的训练中经常使用反向传播算法来高效的计算梯度。

五、反向传播算法

 假设采用随机梯度下降进行神经网络参数学习，给定一个样本（x,y），将其输入到神经网络模型中，得到网络输出为$\hat{y}$。假设损失函数为$y,\hat{y}$，要进行参数学习就需要计算损失函数关于每个参数的导数。
不失一般性，对第l层中的参数$W^{(l)}$和$b^{(l)}$计算偏导数。因为$\frac{\partial \mathcal{L}(y,\hat{y})}{\partial W^{(l)}}$的计算涉及向量对矩阵的微分，十分繁琐，因此我们先计算$\mathcal{L}(y,\hat{y})$关于参数矩阵中每个元素的偏导数$\frac{\partial \mathcal{L}(y,\hat{y})}{\partial w_{ij}^{(l)}}$。根据链式法则，

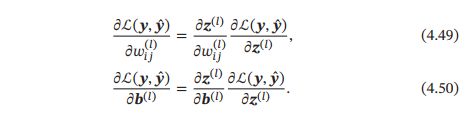
上式中第二项都为目标函数关于第$l$层的神经元$z^{(l)}$的偏导数，称为误差项，可以一次计算得到。这样我们只需要计算三个偏导数，分别为$\frac{\partial z^{(l)}}{\partial {w_{ij}}^{(l)}}$、$\frac{\partial z^{(l)}}{\partial b^{(l)}}$和$\frac{\partial \mathcal{L}(y,\hat{y})}{\partial z^{(l)}}$


从上式可以看出，第l层的误差项可以通过第$l+1$层的误差项计算得到，这就是误差的反向传播（BackPropagation,BP）。
反向传播算法的含义是：第l层的一个神经元的误差项（敏感性）是所有与该神经元相连的第l+1层的神经元的误差项的权重和。然后，再乘上该神经元激活函数的梯度。

在计算出每一层的误差项之后，就可以得到每一层参数的梯度。因此，使用误差反向传播算法的前馈神经网络训练过程可以分为以下三步：
（1）前馈计算每一层的净输入$z^{(l)}$和激活值$a^{(l)}$，直到最后一层；
（2）反向传播计算每一层的误差项${\delta }^{(l)}$
(3)计算每一层参数的偏导数，并更新参数。

六、自动梯度计算

分为三类： 数值微分、符号微分和自动微分
（1）数值微分： 使用数值方法来计算函数$f(x)$的导数。实用性较差，计算复杂度较高。
（2）符号微分：基于符号计算的自动求导方法。符号计算也叫代数计算，是指用计算机来处理带有变量的数学表达式。
（3） 自动微分： 基本原理式所有的数值计算可以分解为一些基本操作，包含+、-，*，/和一些初等函数，exp,log,sin,cos等，然后利用链式法则来自动计算一个复合函数的梯度。

• 静态计算图和动态计算图
  静态计算图是在编译时构建计算图，计算图构建好之后在程序运行时不能改变，而动态计算图是在程序运行时动态构建。两种构建方式各有优缺点。静态计算图在构建时可以进行优化，并行能力强，但灵活性比较差。动态计算图则不容易进行优化，当不同的输入的网络结构不一致时，难以并行计算，但是灵活性比较高。

参考文献

[1] 神经网络与深度学习. 邱锡鹏.