sklearn.ensemble模型融合

模型融合优势

• 降低选错假设导致的风险
• 提升捕捉到真正数据规律的可能性
• 提升具有更好的泛化能力的可能性

常见的模型融合方式

• 均值法Averaging：适用于回归问题
• 投票法Voting：适用于分类模型
• 堆叠法Stacking
• 改进的堆叠法Blending

投票法

硬投票

通过模型预测的结果数量频率分布进行决策

• 相对多数投票：少数服从多数
• 绝对多投票：至少有50％的决策都是同一类别才能输出预测结果，否则拒绝预测，在一定程度上能衡量投票的执行程度。

软投票

通过每个模型给出分类在每个类别的概率，通过某种加权方式进行加和，然后取概率最大的类别作为预测结果。

栗子

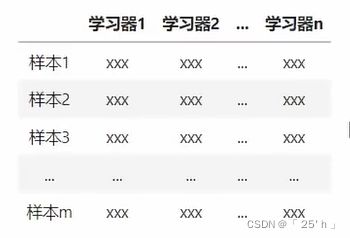
• 对于下面这个预测结果来说，若是硬投票一定是类别3
• 但是若通过软投票通过均值加权方式进行判断的话，类别2的概率最大，那么预测结果就是类别2
• 原因就是在判断为类别2的分类器中，类别2的概率值明显大于类别3，造成置信程度较大。
  
  硬投票加权情况：
  
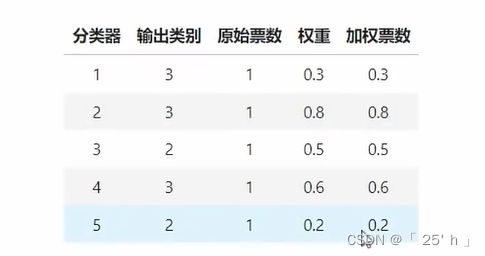
  软投票加权情况：
  
  

sklearn

sklearn.ensemble.VotingRegressor(estimators# 模型列表
								,weights=None # 模型权重
								, n_jobs=None,# 线程数量
								 verbose=False
								 )
                 
sklearn.ensemble.VotingClassifier(estimators, # 投票法进行的分类器以及其名称，多个要使用列表包装
								voting='hard',# 默认硬投票-->相对多数投票，若是"soft"软投票，只能接收输出概率值得模型，SVR类的间隔度模型就不再适用
								weights=None,# 模型权重
                 				n_jobs=None, # 线程数
                 				flatten_transform=True, #见下说明
                 				verbose=False# 模型监控
                 				)

flatten_transform解释：当使用软投票时,可以通过该参数选择输出的概率结构。如果为True，最终则输出结构为(n_samples,n_estimators* n_classes)的二维数组。如果为False，最终则输出结构为(n_samples,n_estimators,n_classes)的三维数组:(n_samples,n_estimators,n_classes)的三维数组。

多样性

单个评估器的结果好于单个算法的关键条件:评估器之间相互独立。评估器之间的独立性越强，则模型从平均/投票当中获得的方差减少就越大，模型整体的泛化能力就越强。
无论是投票法还是平均法，都与Bagging算法有异曲同工之妙，因此我们相信"独立性"也有助于提升投票融合与平均融合的效果。在模型融合当中，独立性被称为"多样性” (diversity)，评估器之间的差别越大、彼此之间就越独立，因此评估器越多样，独立性就越强。完全独立的评估器在现实中几乎不可能实现，因为不同的算法执行的是相同的预测任务，更何况大多数时候算法们都在相同的数据上训练，因此评估器不可能完全独立。但我们有以下关键的手段，用来让评估器变得更多样、让评估器之间相对独立:

• 训练数据多样性：多种有效的特征工程，基本不咋用
• 样本多样性：每次使用部分数据进行训练，主要是看效果
• 特征多样性：使用样本不同的子集训练，数据量较小就会导致模型效果急剧下降，像随机森林和提升树中参数max_features
• 随机多样性：随机种子不同，特征起始点不同，或者使用不同的损失函数。像参数random_state
• 算法多样性（主要）：增加不同类型的算法：集成模型，树模型，概率模型，线性模型，注意：每个模型单独的效果不能过于糟糕，否则模型融合无法弥补。

分类栗子

• 一般来说，我们你在使用模型融合之前，需要通过一个较好的模型对于数据集进行单独的训练，根据样本数据集的大小，复杂度确定不同的模型，轻微调参数，得到一个基准分数，和模型融合分数进行对比，判断融合是否有效
• 对于融合的基础模型，我们一般直接不对其进行调参（默认），等到我们知道了模型是什么样的状态再有目的性的修改参数。
  • 若训练数据集得分明显高于测试集，说明过拟合，我们要对模型进行添加惩罚项（在以下的栗子中直接是调参后的结果，实际上若过拟合应该对于每个模型都要画出学习曲线寻找最优泛化能力的参数组合）
    • 逻辑回归中的 惩罚项系数C
    • KNN中的n_neighbors
    • 决策树、随机森林中的max_depth，max_features，min_impurity_decrease
    • 梯度提升树，xgboost中的max_features，max_depth对于梯度集成树影响力不如max_features

导入库函数

import numpy as np
import pandas as pd
import matplotlib as plt
from sklearn.model_selection import KFold, cross_validate, train_test_split
from sklearn.datasets import load_digits
from sklearn.neighbors import KNeighborsClassifier as KNNC
from sklearn.tree import DecisionTreeClassifier as DTC
from sklearn.linear_model import LogisticRegression as LR
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.ensemble import GradientBoostingClassifier as GBC
from sklearn.ensemble import StackingClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import VotingClassifier

定义模型列表中每个模型结果的函数

def individual_estimators(estimators):
    for estimator in estimators:
        cv = KFold(n_splits=5, shuffle=True, random_state=100)
        res = cross_validate(estimator=estimator[1], X=X_train, y=Y_train,
                             cv=cv, scoring="accuracy", n_jobs=-1, return_train_score=True
                             , verbose=False)
        test = estimator[1].fit(X_train, Y_train).score(X_test, Y_test)
        print(estimator[0]
              , "\n train_score:{}".format(res["train_score"].mean())
              , "\ncv_mean:{}".format(res["test_score"].mean())
              , "\ntest_score:{}\n".format(test))

定义单个模型训练测试结果函数

def fusion_estimators(clf):
    cv = KFold(n_splits=5, shuffle=True, random_state=100)
    res = cross_validate(estimator=clf, X=X_train, y=Y_train,
                         cv=cv, scoring="accuracy", n_jobs=-1, return_train_score=True
                         , verbose=False)
    test = clf.fit(X_train, Y_train).score(X_test, Y_test)
    print(clf
          , "\n train_score:{}".format(res["train_score"].mean())
          , "\ncv_mean:{}".format(res["test_score"].mean())
          , "\ntest_score:{}\n".format(test))

加载和划分数据集

digit = load_digits()
X = digit.data
Y = digit.target
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=100)

通过逻辑回归定基准线

fusion_estimators(LR(max_iter=3000,random_state=100,n_jobs=-1))
"""
LogisticRegression(max_iter=3000, n_jobs=-1, random_state=100) 
 train_score:1.0 
cv_mean:0.9546607221906026 
test_score:0.9722222222222222
"""

多模型创建并查看效果

"""-----------------------------------模型的多样性------------------------------------"""
# 逻辑回归
clf1 = LR(max_iter = 3000,C=0.1,random_state=10,n_jobs=-1)
# 随机森林
clf2 = RFC(n_estimators= 100,max_depth=12,random_state=10,n_jobs=-1)
# 梯度提升树
clf3 = GBC(n_estimators= 100,random_state=1314)#max_features=64
# 决策树（有过随机森林了，也没必要要）
clf4 = DTC(max_depth=8, random_state=1412)# 太拖后腿了，直接不能用，在estimators 中删除了
# KNN算法
clf5 = KNNC(n_neighbors=10,n_jobs=8)
# 朴素贝叶斯算法
clf6 = GaussianNB()# 太拖后腿了，直接不能用，在estimators 中删除了

"""-----------------------------------特征和随机的多样性------------------------------------"""
clf7 = RFC(n_estimators= 100,max_features="sqrt" ,max_samples=0.9,random_state=4869,n_jobs=8)
clf8 = GBC(n_estimators= 100,max_features=16, random_state=4869)
estimators = [("Logistic Regression" ,clf1)
              ,( "RandomForest", clf2)
              # ,("GBDT" ,clf3)这个梯度提升树效果不好，并且慢，所以删了，效果不好的主要原因可能是数据集过于简单，无法发挥集成学习的优势。（，不过clf6的提升树还可以，体现出了特征多样性，随机多样性）
              # ,("Decision Tree",clf4)
              ,("KNN",clf5)
              # ,("Bayes",clf6)
              ,("RandomForest2", clf7)
              ,("GBDT2", clf8)
             ]
individual_estimators(estimators)

保留的五个模型输出的结果

"""
Logistic Regression 
 train_score:1.0 
cv_mean:0.9562480237779042 
test_score:0.9703703703703703

RandomForest 
 train_score:1.0 
cv_mean:0.9697527350913806 
test_score:0.9703703703703703

KNN 
 train_score:0.978121915274522 
cv_mean:0.9737336368810473 
test_score:0.9833333333333333

RandomForest2 
 train_score:1.0 
cv_mean:0.9681496237273131 
test_score:0.9703703703703703

GBDT2 
 train_score:1.0 
cv_mean:0.9697495731360274 
test_score:0.9722222222222222
"""

模型融合

均值投票

clf = VotingClassifier(estimators,voting="soft")
fusion_estimators(clf)
"""
train_score:1.0 
cv_mean:0.9800860051856068 
test_score:0.9888888888888889
"""

加权投票

加权投票是一件非常主观的事情，不过我们通常增加效果较好的模型权值，减小模型相对不好的权值（可以先将权值设置为单个模型在测试集上的分数，在此基础之上通过上述准则进行简单调整）

clf = VotingClassifier(estimators,voting="soft",weights=[0.97,0.97,0.98,0.97,0.97])
fusion_estimators(clf)
"""
train_score:1.0 
cv_mean:0.9800860051856068 
test_score:0.9888888888888889
"""

堆叠法stacking

思想引入

堆叠法本质上就是将投票法的思想转化了一下，之前我们使用投票法取权值时，过去主观，们就有了一种方案：使用一个算法替代这个主观的确定权值的过程，那么这个去定权值的过程就是我们的元学习器。
本质就是寻找最优点融合规则。

投票法和stacking区别

给元学习器提供的数据

• 在分类模型中，我们可以选择每个输出的类别，概率，置信度作为我们的纵向特征：
  • 例子：类别假设有10个，基学习器有5个，若使用概率作为特征值让元学习器学习，就会有$5\ast 10=50$个特征，若使用类别作为元学习器的特征，就有 $5\ast 1=5$个特征，造成数据特别简单，所以最常用的还是概率让元学习器学习以增强数据复杂度，让元学习器捕获更多有效信息。
• 在回归模型中只能输出预测结果，也就是说一个基学习器只能给元学习器一盒特征，所以模型特征量和复杂度远小于分类模型，
• 所以在选择元学习器时，对于分类模型可以选择简单的模型或复杂模型，对于回归模型往往选择简单的元学习器，这样做的目的还是为了防止过拟合，若回归模型使用复杂的模型作为元学习器不过拟合也是可以选择的，一切根据交叉验证的结果进行衡量元学习器的好坏，不是绝对的
• 另外基学习器本身的模型复杂度一般较高，也有简单的模型可以特高多样性，但是不能存在过拟合的现象，因为模型融合本身就是一个容易过拟合的方法。

下面就是基学习器给元学习器提供的特征数据。

stacking中的交叉验证

对于一开始的数据我们拿出去了30%作为了测试集，在训练过程中无法使用，另外在基学习器给stacking时就只有了70%，然后如果在分出30%作为测试集用于stacking模型训练中的测试，最后就是有49%作为了训练数据样本，很显然，数据量太少了，为了保证元学习器具有较多的样本量，我们通过让每个基学习器分别训练cv次（超参数）那70%到数据，然后组成该基学习器给元学习器的一个或一组特征数据，然后将每个基学习器生成的数据特征并在一起就组成了所有的元学习器的数据。然后使用者全部的数据通过元学习器进行模型训练。

sklearn中Stacking参数

# 回归相对于分类只是没有stack_method参数
sklearn.ensemble.StackingRegressor(estimators
                                   , final_estimator=None
                                   , cv=None
                                   , n_jobs=None
                                   , passthrough=False
                                   , verbose=0)

sklearn.ensemble.StackingClassifier(estimators  # 基学习器列表[("自定义名称",模型),....]
                                    , final_estimator=None  # 元学习器模型
                                    , cv=None  # 交叉验证次数，较大时不容易过拟合但学习能力有所下降，当然也存在瓶颈，太大浪费时间
                                    , stack_method='auto'
                                    # 将基学习器的什么特征给元学习器(auto:按照最优的选择)，概率(predict_pro)，置信度(decision_function)，类别(predict)
                                    # 
                                    , n_jobs=None  # 线程数
                                    , passthrough=False  # 是否将原始数据的特征加在元学习器中作为元学习器训练数据特征的一部分
                                    , verbose=0)  # 监控模型训练程度，0表示不输出，1：带进度条的输出日志信息，2：不带进度条的输出日志信息

训练测试总流程

注意事项

• 对于基学习器粗调参，不能过拟合，元学习器精调。
• 注意基学习器的多样性，泛化能力，运算时间
• 基学习器和元学习器尽量使用相同的收敛函数和评估指标，让整体模型朝着一个方向收敛。

stacking接着上一个例子

# 元学习器使用随机森林
final_estimator = RFC(n_estimators=100,min_impurity_decrease=0.0025
                      ,random_state=100,n_jobs=-1)

scf=StackingClassifier(estimators=estimators,final_estimator=final_estimator,n_jobs=-1)

"""
train_score:1.0 
cv_mean:0.982479605387972 
test_score:0.9851851851851852
"""

实际上堆叠法应该比一般方法效果好，不过这次我们使用的数据集较为简单，不能正真体现出来stacking堆叠法的优势，这也在一定成程度上说明简单的魔性没必要使用模型融合和更容易过拟合的堆叠法。

知识点—>查看随机森林每一棵树的深度

from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.datasets import load_digits

digit = load_digits()
X = digit.data
Y = digit.target
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=100)
clf2 = RFC(n_estimators= 100,max_depth=12,random_state=10,n_jobs=-1)
clf2.fit(X_train,Y_train)# 数据和之前
# clf2.estimators_就是树模型的集合就是单个决策树DecisionTreeClassifier
# tree_就是参数集合.max_depth就是最大深度
for i in clf2.estimators_[:]:
    print(i.tree_.max_depth)