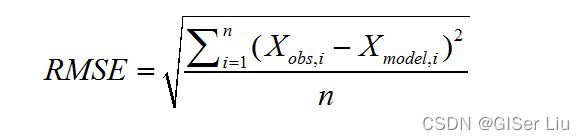机器学习系列6 使用Scikit-learn构建回归模型:简单线性回归、多项式回归与多元线性回归
本文所用数据均可免费下载
ps:1万多字写了四天,累死我了;如有错别字请评论告诉我。创作不易,恳请四联
目录
一、内容介绍
二、理论实践
1.学习准备
①数据准备
②运行环境
2.提出问题
3.线性回归概念及数学原理
①简单线性回归理论
②多项式线性回归理论
③多元线性回归理论
4.相关系数概念
5.寻找相关性
6.分类特征变量的处理
6.简单线性回归
①调用Python库
②数据格式转换
③划分数据集
④训练模型
⑤模型评估
⑥南瓜种类回归
7.多项式回归
①销售日期-南瓜价格
②南瓜种类-南瓜价格
8.多元线性回归
①数据准备
②划分数据集
③训练模型
④评估模型
⑤多元线性回归(多项式)
三、内容总结
一、内容介绍
在前一篇文章中,我们已经在南瓜定价数据集的示例数据中探索了线性回归,本文中我们将使用之前处理好的数据比较简单线性回归、多项式线性回归以及多元线性回归。并使用Matplotlib库对其进行可视化。
现在,你已经准备好更加深入的了解机器学习的回归。虽然可视化可以让你更好的理解数据,但机器学习的真正力量来自于训练模型。机器学习模型通过历史数据(先验知识)进行训练以自动捕获(寻找)数据间的依赖关系(规律),并通过此规律预测新输入的结果。
在本文中,我将带你了解三种回归类型:简单线性回归、多项式回归以及多元线性回归。以及这些技术背后的一些数学知识。这些不同的模型将使我们能够根据不同的输入数据预测南瓜价格。
在整个课程中,为了使本文的受众更广,文章中尽量避免了数学知识,但为了更好的学习效果,请大家多多注意图表,标注和其他学习工具,以帮助理解。
二、理论实践
1.学习准备
①数据准备
你现在应该熟悉我们正在研究的南瓜数据的结构。你可以在上一篇文章中得知它已经过预处理。数据已经上传到我的资源,免费下载即可。
输入以下代码:查看本文需要的数据:
import pandas as pd#调用pandas库并命名为pd
new_pumpkins =pd.read.csv("new_pumpkins.csv")#利用pandas库打开csv数据
print(new_pumpkins.head())#查看数据的前5行
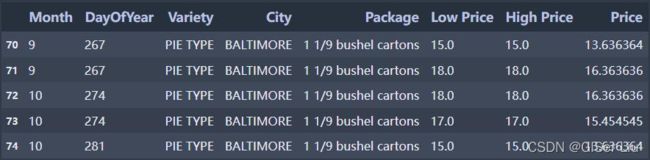
new_pumpkins.info() #查看数据组织结构图1 new_pumpkins
在图1中我们查看之前处理好的new_pumpkins数据,其中的DayOfYear列表示销售日期,如267代表一年中的第267天,这是为了按天数可视化数据。计算代码如下:
day_of_year = pd.to_datetime(pumpkins['Date']).apply(lambda dt: (dt-datetime(dt.year,1,1)).days)图2 数据组织结构
查看数据结构,可以看出销售日期DayOfYear是数值类型,南瓜种类Variety是Object类型。
②运行环境
开发环境依旧是Jupyter notebook,安装方法可见前文。
2.提出问题
在你开始练习之前,提出你的问题。
0 什么时候是购买南瓜的最佳时间?
1 我如何预测一箱迷你南瓜的价格?
2 我应该在用1/2 bushel的篮子里买它们,还是用10/9 Bushel的篮子买?让我们继续深入研究这些数据。(buhsel是体积测量的单位)
3.线性回归概念及数学原理
线性回归包括简单线性回归(一元线性回归)、多项式回归、多元线性回归。
简单线性回归可以看作是次数和特征数量为1的多元线性回归。多项式回归也可以转化为多元线性回归。
之前我们学到:线性回归练习的目标是能够绘制一条回归线来。且:
0 显示变量关系。显示变量之间的关系
1 进行预测。准确预测新数据点与该线的关系。
最小二乘回归就是绘制回归线的常用方法。最小二乘法(Least squares)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳匹配函数。利用最小二乘法可以方便地求得未知的线性函数,并使得线性函数拟合的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其核心就是保证所有数据偏差的平方和最小。
使用最小二乘法是因为我们想要对一条距离所有数据点的累积误差最小的线进行建模。我们对误差进行平方是因为我们关注的是误差的大小而不是方向。
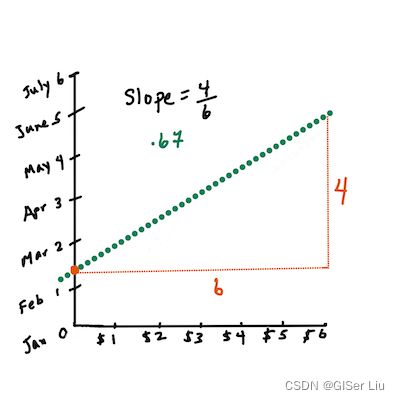
图3 线性回归
最小二乘回归线也称为最佳拟合线,可以用一个式子来表示:
Y = wX + b
X是“自变量”。 Y是“因变量”。直线的斜率是w,也称权重或系数;a 是 Y的截距,也称常数项系数。
这与我们初中所学的斜线方程并无区别,原理一样:
Y = kX + b
(k是斜率,b是截距)
在这里我们思考一下,因为监督分类是有训练的机器学习,因此我们训练的数据中已经包括了特征变量X与预测标签Y,我们基于最小二乘回归模型需要求解的参数只有w与b。那么我们训练此模型的流程就可以分为:
0 计算斜率与截距
1 测试评估模型
随着特征变量的增多,我们需要计算的w(系数或斜率)也增多,截距或常量b则始终只有一个。
回忆之前南瓜数据的原始问题:“按月预测每bushel(体积单位)南瓜的价格”,是指将月份作为自变量X。将南瓜价格作为因变量Y。根据拟合出的回归线,我们便可根据月份预测出当月的南瓜价格。反之,如果知道南瓜价格,也能预测出月份!但预测结果不仅取决于斜率w,也取决于截距b。
你可以在这个网站输入数据点来拟合回归线,或者使用Excel尝试。
①简单线性回归理论
我们以及了解了线性回归的数学原理,所谓简单线性回归,就是单变量的线性回归,如销售日期与南瓜价格的线性关系或南瓜种类与南瓜价格的线性关系,简单线性回归的回归线是一条直线。它可以单方面的探索特征间的相关性。
②多项式线性回归理论
虽然变量之间有时存在线性关系 。如南瓜体积越大,价格越高;但并不是所有的关系都是呈现线性,在这种情况下一元线性回归拟合出来的回归线欠拟合,不能很好的预测价格。因此我们可以采用多项式回归,
在数学中,多项式(polynomial)是指由变量、系数以及它们之间的加、减、乘、幂运算(非负整数次方)得到的表达式。如若给定两个输入特征变量 X 和 Y,一次多项式表示输入特征为X,Y;二次多项式表示增X^2、XY 和 Y^2三个特征。以此类推。
多项式中的每个单项式叫做多项式的项,这些单项式中的最高项次数,就是这个多项式的次数。单项式由单个或多个变量和系数相乘组成,或者不含变量,即不含字母的单个系数(常数)组成,这个不含字母的项叫做常数项。
多项式回归模型创建的曲线可以更好地拟合非线性数据。在我们的例子中,如果我们在输入数据中包含一个平方变量如x^2,我们就可以用抛物线曲线来拟合我们的数据,我们也知道该抛物线在一年中的某个时候将具有最小值或者最大值。
多项式回归算法并没有新的特点,完全是使用线性回归的思路,关键在于为数据添加新的特征,而这些新的特征是原有的特征的多项式组合,采用这样的方式就能解决非线性问题。这样的思路跟PCA这种降维思想刚好相反,而多项式回归则是升维,添加了新的特征之后,使得更好地拟合高维数据。这类似于走迷宫,在迷宫里走效率低,从高空看迷宫则简单的多。
在这里我们使用Scikit-learn中封装的两个函数来简化代码量:
0 make_pipeline()
1 PolynomialFeatures()
make_pipeline()可以将许多算法模型串联起来,把多个estamitors级联成一个estamitor,比如将特征提取、归一化、分类组织在一起形成一个典型的机器学习问题工作流。这类似与ArcGIS中的模型构建器。在本此学习中,我们将创建一个pipeline,将多项式特征添加到我们的模型中,然后训练回归模型。
PolynomialFeatures()函数可以通过输入的变量来创建新特征,其中的参数表示多项式的次数。
③多元线性回归理论
多元,即特征向量不唯一,这与多项式回归类似;实际上多项式回归也可以转化为多元线性回归。
从式中可以看出,随着特征变量X的增多,我们需要计算的w系数也增加。这与简单线性回归原理区别不大,只是拟合出来的回归线是曲线。多元回归线往往有更好的相关性,但也要注意避免过拟合。
4.相关系数概念
相关系数是表示自变量与因变量之间相关程度的系数,其取值区间为(0,1),越靠近1相关系数越高;1为完全相关,0为完全不相关;我们可以使用散点图来可视化此系数。聚集在回归线周围的数据点具有高度相关性,分散在回归线周围的数据点具有低相关性。
一个优秀的线性回归模型是使用最小二乘回归方法且数据具有高度相关性。
5.寻找相关性
现在你已经了解了线性回归背后的数学原理,让我们尝试寻找数据的相关性,看看我们是否可以预测哪类南瓜价格最佳。
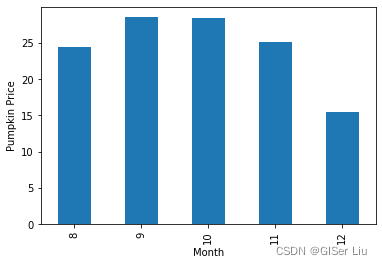
从上一篇文章中,你可能已经看到不同月份的平均价格如下所示:
图4 月份-价格直方图
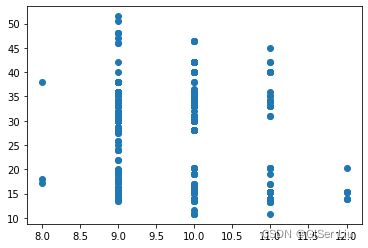
图5 月份-价格散点图
这表明月份与价格应该有相关性,我们可以进一步尝试查看销售日期-价格之间关系的散点图。输入以下代码:
import matplotlib.pyplot as plt
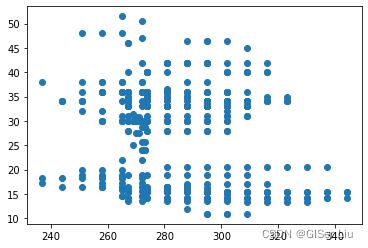
plt.scatter('DayOfYear','Price',data=new_pumpkins) #DayOfYear为销售日期,绘制销售日期与价格的散点图图6 销售日期-价格散点图
看起来似乎有不同的价格群对应于不同的南瓜品种。为了证实这一假设,我们使用不同的颜色绘制每个南瓜类别。输入以下代码并查看结果:
ax=None
colors = ['red','blue','green','yellow']
for i,var in enumerate(new_pumpkins['Variety'].unique()):
df = new_pumpkins[new_pumpkins['Variety']==var]
ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var)图7 销售日期-价格按不同南瓜种类分色散点图
根据图7,我们可以看到品种对整体价格的影响比销售日期更大。因此,让我们暂时只关注一种南瓜品种,看看日期对价格有什么影响,以下代码用以取出南瓜类型为‘PIE TYPE’的数据并绘制销售日期-价格散点图:
pie_pumpkins = new_pumpkins[new_pumpkins['Variety']=='PIE TYPE']
pie_pumpkins.plot.scatter('DayOfYear','Price')图8 销售日期-价格‘PIE’南瓜散点图
如果我们现在利用模型计算相关系数,我们将得到类似的结果 。这意味着训练预测模型是有意义的。
在训练线性回归模型之前,确保数据是清理过的,这很重要!线性回归不能很好地处理缺失值,因此需要删除缺失值,下面代码用以删去缺失值所在数据以及查看新数据组织结构:
pie_pumpkins.dropna(inplace=True)
另一种方法是用相应列中的平均值填充这些空值,类似插值。
6.分类特征变量的处理
我们希望能够使用相同的模型预测不同南瓜品种的价格。但是,南瓜类型列与其他特征略有不同,因为它的值是字符串而非数值。此类列我们称为分类列。
为了方便训练,我们首先需要将其转换为数值形式,对其进行编码:
get_dummies()函数将用 4 个不同的列替换原有列,每个列对应一个品种。每列将包含相应的行是否属于给定的种类,这意味着线性回归中将有四个系数,每个南瓜品种一个,负责该特定品种的“起始价格”。
下面的代码将对各种南瓜进行一键编码,查看编码后南瓜数据的结构:
X = pd.get_dummies(new_pumpkins['Variety'])
print(X.info())图9 按南瓜类型编码
我们可以看出南瓜数据被分为四类,各包含415个样本。
按照不同南瓜类型绘制的回归线并无意义,其横轴值表示类别而非回归值。因此无需进行绘制。
6.简单线性回归
为了训练我们的线性回归模型,我们将使用 Scikit-learn 库分别尝试单一变量的简单线性回归与多元简单线性回归。
①调用Python库
首先,输入以下代码,调用我们需要的python第三方库:
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split②数据格式转换
接着,我们将输入值(特征变量)和预期的输出值(预测标签)分离到单独的 numpy 数组中,输入以下代码:
X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1)
Y = pie_pumpkins['Price']请注意,我们必须对输入数据执行操作,以便线性回归库正确理解它。线性回归需要一个二维数组作为输入,其中数组的每一行都对应于输入要素的向量。在我们的例子中,由于我们只有一个输入 -,因此我们需要一个形状为N×1的数组,其中N是数据集大小。
③划分数据集
然后,我们需要将数据集拆分为训练集和测试集,以便在训练后验证模型:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
④训练模型
最后,训练线性回归模型只需要两行代码。我们实例化一个LinearRegression()对象lin_reg,并输入以下代码用训练集拟合出我们的线性回归模型:
lin_reg = LinearRegression() #实例化对象
lin_reg.fit(X_train,y_train) #训练线性回归模型经过训练的LinearRegression()对象包含回归的所有系数,我们可以使用对象属性访问这些系数。本次案例中只有相关系数。
⑤模型评估
为了评估模型的精度,我们在测试数据集上预测价格,然后计算预测价格与实际价格的误差。这可以使用均方误差 (RMSE) 指标来完成,它是预期值和预测值之间所有平方差的平均值(数学期望)的平方根,它的本质是在MSE上做了一个开根号,这样做是为了将评估值的量纲和原值的量纲保持一致。
下面是RMSE指标的计算代码:
pred = lin_reg.predict(X_test)
mse = np.sqrt(mean_squared_error(y_test,pred)) #mean_squared_error用于计算MSE
print(f'RMSE指标: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)')评估模型质量的另一个指标是相关系数,利用score()函数获得。相关系数计算代码如下:
score = lin_reg.score(X_train,Y_train)
print('相关系数: ', score)
plt.scatter(X_test,Y_test)
plt.plot(X_test,pred)如果相关系数值为 0,则表示模型不考虑输入数据,预测的效果最差。值 1 意味着我们可以完美地预测所有预期的输出。我们还可以将测试数据与回归线一起绘制。输出结果为:
RMSE指标: 2.77 (17.2%)
相关系数: 0.04460606335028361图10 简单线性回归图
在我们的例子中,我们的误差似乎在3点左右,约为17%。并不是很好。相关系数约为0.04,这是相当低的。
⑥南瓜种类回归
根据图7的结果与分类特征变量的预处理我们可以尝试用不同的南瓜类型来检验南瓜类型与价格的相关性,输入代码,查看结果:
X = pd.get_dummies(new_pumpkins['Variety']) #以南瓜的类别作为特征变量,并转化数据类型
Y = new_pumpkins['Price'] #以价格为预测标签
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)#以8:2的比例划分数据集与训练集
lin_reg = LinearRegression()#构建线性回归模型对象
lin_reg.fit(X_train,Y_train)#训练模型
pred = lin_reg.predict(X_test)#将测试集上的预测值存储在pred中
rmse = np.sqrt(mean_squared_error(Y_test,pred))#计算均方误差
print(f'RMSE指标: {rmse:3.3} ({rmse/np.mean(pred)*100:3.3}%)')#输出均方误差的值以及错误率
score = lin_reg.score(X_train,Y_train)#计算回归系数
print('相关系数: ', score)#输出回归系数的值结果如下:
RMSE指标: 5.24 (19.7%)
相关系数: 0.774085281105197我们可以看到,虽然RMSE指标变化不大,但数据间的相关性提升到了0.77,这与我们猜想的一样,南瓜价格与南瓜品种的相关性高于销售日期。
再看一下销售日期和价格之间的关系。这个散点图必须用一条直线来拟合吗?价格不能波动吗?在这种情况下,我们可以尝试多项式回归。
7.多项式回归
①销售日期-南瓜价格
多项式回归前期数据准备工作与简单线性回归并无区别,关键在于对输入特征变量进行多项式。利用我们了解的多项式回归理论及工具构建流程化工具pipeline,在我们的例子中,我们使用输入数据中的二阶多项式X,X^2来构建回归模型。如果需要,我们也可以使用更高阶多项式。输出以下代码查看图像与精度:
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression())#构建自动化流程
pipeline.fit(X_train,Y_train)#训练模型
pred = pipeline.predict(X_test)#在测试集上预测结果并保存在pred变量中
rmse = np.sqrt(mean_squared_error(Y_test,pred))#计算RMSE
print(f'RMSE指标: {rmse:3.3} ({rmse/np.mean(pred)*100:3.3}%)')
score = pipeline.score(X_train,Y_train)#计算相关系数
print('相关系数: ', score)
plt.scatter(X_test,Y_test)#绘制散点图
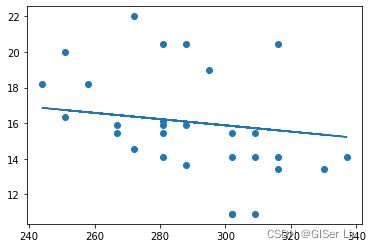
plt.plot(X_test,pred)#绘制回归线,若多条回归线是因为X_test是随机未排序的,排序后可尝试解决RMSE指标: 2.73 (17.0%)
相关系数: 0.07639977655280128图11 多项式回归
使用多项式回归,我们可以获得略低的MSE和更高的确定性,但依旧很低。我们需要考虑其他特征!
你可以看到,最小的南瓜价格是在万圣节前后观察到的。如何解释这一点?
②南瓜种类-南瓜价格
同理,将南瓜类别代入多项式回归,输入以下代码,我们可以得到其相关性高达0.76。
X = pd.get_dummies(new_pumpkins['Variety'])
Y = new_pumpkins['Price']
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)#以8:2的比例划分数据集与训练集 # setup and train the pipeline
pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression())#构建流程化工具,其中PolynomialFeatures(2)是对输入数据进行2次多项式拟合,后者为构建线性回归模型
pipeline.fit(X_train,Y_train)
pred = pipeline.predict(X_test)
rmse = np.sqrt(mean_squared_error(Y_test,pred))
print(f'RMSE指标: {rmse:3.3} ({rmse/np.mean(pred)*100:3.3}%)')
score = pipeline.score(X_train,Y_train)
print('相关系数: ', score)结果为:
RMSE指标: 5.2 (19.5%)
相关系数: 0.75900493649344238.多元线性回归
在了解多项式回归以后,我们理解多元线性回归就简单的多。多元,即多个特征,多项式是基于输入特征生成特征,而多元既可以表示1-n个生成的特征,也表示输入的特征,在本次练习中,多元表示考虑到多个因素,如:销售日期、销售地区、南瓜种类等等因素。基于多种特征变量回归的特征曲线拟合出来的机器学习模型更加适用于实际操作:
①数据准备
代码的其余部分与我们上面用于训练线性回归的代码相同。为了获得更准确的预测,我们需要考虑更多的分类特征,代码如下:
X = pd.get_dummies(new_pumpkins['Variety']) \
.join(new_pumpkins['Month']) \
.join(pd.get_dummies(new_pumpkins['City'])) \
.join(pd.get_dummies(new_pumpkins['Package']))
Y = new_pumpkins['Price']②划分数据集
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)③训练模型
lin_reg = LinearRegression()#构建线性回归模型对象
lin_reg.fit(X_train,Y_train)#训练模型④评估模型
pred = lin_reg.predict(X_test)#将测试集上的预测值存储在pred中
rmse = np.sqrt(mean_squared_error(Y_test,pred))#计算均方误差
print(f'Mean error: {rmse:3.3} ({rmse/np.mean(pred)*100:3.3}%)')#输出均方误差的值以及错误率 score = lin_reg.score(X_train,Y_train)#计算回归系数
print('Model determination: ', score)#输出回归系数的值输出结果为:
RMSE指标: 2.85 (10.6%)
相关系数: 0.9399208232885795效果很好!相关性已经达到了0.94!!!
⑤多元线性回归(多项式)
为了制作最佳模型,我们可以将上述示例中的组合数据与多项式回归一起使用。为方便起见,以下是完整的代码:
X = pd.get_dummies(new_pumpkins['Variety']) \
.join(new_pumpkins['Month']) \
.join(pd.get_dummies(new_pumpkins['City'])) \
.join(pd.get_dummies(new_pumpkins['Package']))
Y = new_pumpkins['Price']
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression())
pipeline.fit(X_train,Y_train)
pred = pipeline.predict(X_test)
rmse = np.sqrt(mean_squared_error(Y_test,pred))
print(f'RMSE指标: {rmse:3.3} ({rmse/np.mean(pred)*100:3.3}%)')
score = pipeline.score(X_train,Y_train)
print('相关系数: ', score)输出结果为:
RMSE指标: 2.23 (8.26%)
相关系数: 0.9642424355544598我们得到了接近97%的最佳相关系数,RMSE=2.23(~8%的预测误差)。
下面是我们今天创建的不同线性回归模型的性能列表:
| 线性回归类型 |
RMSE |
相关系数 |
| DayOfYear简单线性回归 |
2.77 (17.2%) |
0.04 |
| DayOfYear多项式回归 |
2.73 (17.0%) |
0.08 |
| Variety简单线性回归 |
5.24 (19.7%) |
0.77 |
| Variety多项式回归 |
5.2(19.5%) |
0.76 |
| 多元简单线性回归 |
2.84 (10.5%) |
0.94 |
| 多元多项式线性回归 |
2.23 (8.25%) |
0.97 |
干的好!我们在练习中创建了六个回归模型,并将模型质量提高到 97%。
三、内容总结
在本文中,我们学到了三种类型的线性回归概念及其数学原理。并以南瓜销售为例,完整的讲解了问题思考,数据准备,模型构建及评估流程,并将精度提高到97%。在下一篇文章中我将介绍逻辑回归的原理及代码实践。
挑战
在此练习中测试几个不同的特征变量,查看其相关性。
课后测验
构建模型
如果觉得我的文章对您有帮助,三连+关注便是对我创作的最大鼓励!
“本站所有文章均为原创,欢迎转载,请注明文章出处:https://blog.csdn.net/qq_45590504/category_11752103.html?spm=1001.2014.3001.5482百度和各类采集站皆不可信,搜索请谨慎鉴别。技术类文章一般都有时效性,本人习惯不定期对自己的博文进行修正和更新,因此请访问出处以查看本文的最新版本。”