数据挖掘计算题-1

一、设某事务项集构成如下表，填空完成表1中支持度和置信度的计算（1--12）（15分）。

表1 支持度与置信度

事务ID	项集	L2	支持度%	规则	置信度%
T1	A,D	A,B	（1）	A→B	（7）
T2	D,E	A,C	（2）	C→A	（8）
T3	A,C,E	A,D	（3）	A→D	（9）
T4	A,B,D,E	B,D	（4）	B→D	（10）
T5	A,B,C	C,D	（5）	C→D	（11）
T6	A,B,D	D,E	（6）	D→E	（12）
T7	A,C,D	…		…
T8	C,D,E
T9	B,C,D

PS:置信度计算在A中，同时也含有B的概率(即：if A ,then B的概率),即 Confidence(A➡B)=P(B|A)

支持度计算在所有的交易集中，既有A又有B的概率，即Support(A➡B)=P(AB)。

答案：

(1) 33.3 (2) 33.3 (3) 44.4 (4) 33.3 (5) 33.3 (6) 33.3

(7) 50.0 (8) 60.0 (9) 66.7 (10) 75.0 (11) 60.0 (12) 42.9

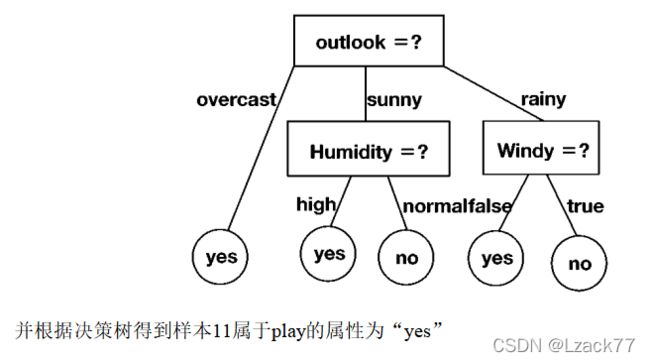
二、给定如表2所示的数据样本集，使用信息增益作为属性度量构造决策树，并对最后一个未知样本进行分类，请写出计算过程并绘制决策树（当决策树的叶子节点只包含一种数据类型时则不再划分），最后根据决策树判断分类结果（共20分） 

提示：（计算结果保留小数点后三位）

 

            计算过程：

首先计算根结点信息熵：

10个样例，正例（yes）占p1=3/5   反例（no）占p2=2/5

计算出当前属性集合{Outlook,Temperature,Humidity,Windy}中每个属性的信息增益。

（1）Outlook

有三种可能取值{sunny,rainy,overcast}，设为D1,D2,D3

D1包含编号{1，2，8，9}，其中正例占p1=1/4，反例占p2=3/4

D2     {4，5，6，10}      p1=3/4    p2=1/4

D3     {3,7}    p1=1    p2=0

 (2)Temperature

{hot,cool,mild}      D1,D2,D3

D1   {1,3}     p1=1/2   p2=1/2

D2    {2,5,6,7,9}     p1=3/5    p2=2/5

D3     {4,8,10}     p1=2/3     p2=1/3

Gain(D,Temperature)=0.010

（3）Humidity

{high,normal}  D1,D2

D1       {1,2,3,4,8}     p1=2/5       p2=3/5

D2       {5,6,7,9,10}   p1=4/5    p2=1/5

Gain(D,Humidity)=0.125

(4)Windy

{true,false}    D1,D2

D1      {2,6,7}       p1=1/3     p2=2/3

D2       {1,3,4,5,8,9,10}     p1=5/7     p2=2/7

Gain(D,Windy)=0.092

此时可知Gain(D,Outlook)=0.322最大，于是有

此时查看原表格发现Outlook的overcast属性对应的结果全是yes，而rainy和sunny既有yes也有no，因此对rainy和sunny再做信息熵计算。（Temperature信息熵太低应该排除吗？）

rainy{4,5,6,10}   sunny{1,2,6,8}

rainy-(1)Temperature

在{4，5，6，10}中Temperature有mild，cool，设为D1,D2

D1    {5，6}     p1=1/2      p2=1/2       Ent(D1)=1

D2    {4,10}      p1=1    p2=0           Ent(D2)=0

Gain_1=X(这个数我不确定是0.971还是0.322，但是公式与X关系不大)-(1/2)*1-(1/2)*0=X-0.5

另外Temperature应不应该排除？暂且不表

rainy-(2)Humidity

{high,normal}      设为D1,D2

D1         {4}           p1=1     p2=0       (貌似p1=1或0这种情况可以直接拿来判断，画进树里做为一边的分支了)

D2        {5,6,10}          p1=2/3       p2=1/3

Gain_2=X-0-(1/2)*0.918=X-0.459

rainy-(3)Windy

{true,false}             设为D1,D2

D1          {6}         p1=0        p2=1

D2        {4,5,10}     p1=1       p2=0        (直接解放)

Gain_3=X-0-0=X

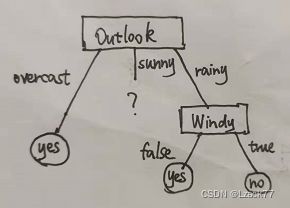
Gain_3信息熵最大，因此选Windy做为rainy的树结点，因为Windy已经可以直接进行判断无需再进行属性分支，现在的决策树是这样：

下一步继续对之前的sunny做分支，过程类似rainy,这里不写了

答案：