【20200408】数据挖掘DM课程课业打卡五之决策树&求解信息增益

叮嘟！这里是小啊呜的学习课程资料整理。好记性不如烂笔头，今天也是努力进步的一天。一起加油进阶吧！

一、填空题

1、数据的属性已知，数据的类别也已知，这样的数据叫做____样本。

正确答案：  训练

2、数据的属性已知，数据的类别未知，这样的数据叫做_____样本。

正确答案：   测试

3、

已知训练数据集如表1：
该数据集中，P(yes)= _____ ； P(no)= _____ ；

该数据集的熵为 Info(D) = _____ ；

（说明：熵可以写成I(m,n)的形式，或者写成-(b/a)*log2(b/a) -( d/c)*log2(d/c)的形式 其中，分数b/a、d/c约分为最简形式）

正确答案：【形式不唯一】

第一空： 
6/10；3/5；0.6

第二空： 
4/10；2/5；0.4

第三空： 
I(6,4)；–(3/5)log2(3/5)–(2/5)log2(2/5)；–(3/5)*log2(3/5)–(2/5)*log2(2/5)；–(2/5)log2(2/5)–(3/5)log2(3/5)；–(2/5)*log2(2/5)–(3/5)*log2(3/5)

4、接上题，已知训练数据集如表1。若以Attribute1为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应Attribute1=V1a，Attribute1=V1b，Attribute1=V1c。三个子集的样本数量与原始数据集的比例分别为 _____ 、 _____ 、 _____ 。

正确答案：0.4；0.2；0.4；

5、接上题，已知训练数据集如表1。若以Attribute1为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应Attribute1=V1a，Attribute1=V1b，Attribute1=V1c。三个子集的熵分别为 _____ 、 _____ 、 _____ 。

（说明：熵可以写成I(m,n)的形式，或者写成-(b/a)*log2(b/a) -( d/c)*log2(d/c)的形式 其中，分数b/a、d/c约分为最简形式）

正确答案：【形式不唯一】

第一空： 
I(1,3)；I(3,1)； – (1/4)log2(1/4)–(3/4)log2(3/4)；–(1/4)*log2(1/4)–(3/4)*log2(3/4)； – (3/4)log2(3/4)–(1/4)log2(1/4)；–(3/4)*log2(3/4)–(1/4)*log2(1/4)

第二空： 
I(2,0)；I(0,2)；– 1log2(1)；– 1*log2(1)；0

第三空： 
I(1,3)；I(3,1)； – (1/4)log2(1/4)–(3/4)log2(3/4)；–(1/4)*log2(1/4)–(3/4)*log2(3/4)； – (3/4)log2(3/4)–(1/4)log2(1/4)；–(3/4)*log2(3/4)–(1/4)*log2(1/4)  

6、接上题，已知训练数据集如表1。若以Attribute1为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应Attribute1=V1a，Attribute1=V1b，Attribute1=V1c。该划分的期望信息为_____ 。

（答案写成 (b/a) I(m,n)+(d/c) I(m,n) 的形式 。其中，分数b/a、d/c约分为最简形式）

正确答案：【形式不唯一】
(2/5)*I(1,3)+(1/5)*I(2,0)+(2/5)*I(3,1)；
(4/5)*I(1,3)+(1/5)*I(2,0)；(4/5)*I(3,1)+(1/5)*I(2,0)；(1/5)*I(2,0)+(4/5)*I(3,1)；(1/5)*I(2,0)+(4/5)*I(1,3)；(4/5)*I(1,3)；(4/5)*I(3,1)；(2/5)*I(1,3)+(2/5)*I(3,1)；(2/5)*I(3,1)+(2/5)*I(1,3)  

7、接上题，已知训练数据集如表1。若以Attribute1为分裂属性，将数据集分成三个子集D1、D2、D3，分别对应Attribute1=V1a，Attribute1=V1b，Attribute1=V1c。该划分的信息增益为 _____ 。

（信息增益用包含 I(m,n)的式子表示 ）

正确答案：【形式不唯一】
I(6,4)-((2/5)*I(1,3)+(1/5)*I(2,0)+(2/5)*I(3,1))；
I(6,4)-(2/5)*I(1,3)-(1/5)*I(2,0)-(2/5)*I(3,1)；I(6,4)-((4/5)*I(1,3)+(1/5)*I(2,0))；I(6,4)-(4/5)*I(1,3)-(1/5)*I(2,0)；I(6,4)-((4/5)*I(3,1)+(1/5)*I(2,0))；I(6,4)-(4/5)*I(3,1)-(1/5)*I(2,0)；I(6,4)-((1/5)*I(2,0)+(4/5)*I(3,1))；I(6,4)-(1/5)*I(2,0)-(4/5)*I(3,1)；I(6,4)-((1/5)*I(2,0)+(4/5)*I(1,3))；I(6,4)-(1/5)*I(2,0)-(4/5)*I(1,3)

二、知识点巩固

1、分类相关概念

 分类：分类任务就是通过训练（或学习），得到一个目标函数或分类规则，把未知类别的数据对象（测试样本）划分到预定义的类别中。
分类任务包含两个步骤：1.训练；2.测试（分类）

 训练：对于其属性和类别都已知的数据对象（即训练样本），通过寻找其中的规律，得到一个目标函数或分类规则的过程。

 测试（分类）：训练完成后，根据得到的目标函数或分类规则，将未知类别的数据对象（测试样本）划分到预定义的类别中。

 训练样本：训练过程中所使用的属性和类别都已知的数据对象即为训练样本。训练过程通过寻找其中的规律，得到一个目标函数或分类规则。

 测试样本：测试过程中所使用的，属性值已知但类别未知的数据对象即为测试样本。测试过程目标函数或分类规则，预测每个测试样本的类别。

2、解决分类问题的一般方法

基本概念：
 训练集：数据库中为建立模型而被分析的数据元组形成训练集。
 训练集中的单个元组称为训练样本,每个训练样本有一个类别标记。
 一个具体样本的形式可为:( v1, v2, …,vn; c );其中vi表示属性值,c表示类别。
 测试集（检验集）：用于评估分类模型的准确率。

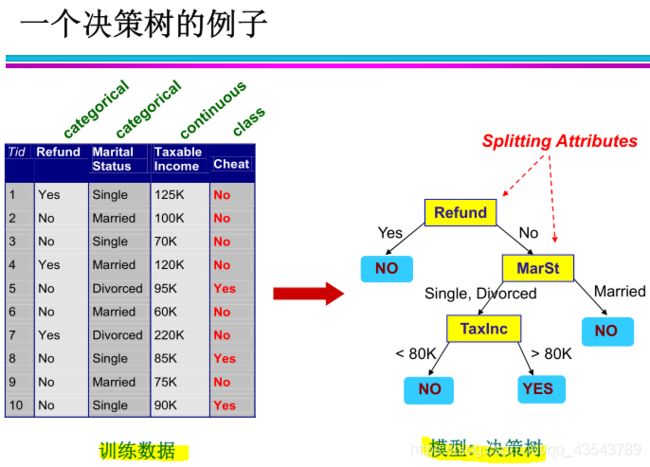
3、用决策树归纳分类

什么是决策树？

– 类似于流程图的树结构
– 每个内部节点表示在一个属性上的测试
– 每个分枝代表一个测试输出
– 每个树叶节点代表类或类分布

决策树的生成由两个阶段组成：

– 决策树构建（重点）
 开始时，所有的训练样本都在根节点
 递归的通过选定的属性，来划分样本 （必须是离散值）

– 树剪枝（略）
 许多分枝反映的是训练数据中的噪声和孤立点，树剪枝试图检测和剪去这种分枝。

决策树的使用：

对未知样本进行分类
– 通过将样本的属性值与决策树相比较

为了对未知数据对象进行分类识别 ， 可以根据决策树的结构对数据集中的属性进行测试 ， 从决策树的根节点到叶节点的一条路径就形成了相应对象的类别测试 。 决策树可以很容易转换为分类规则。

从同一个训练数据集构建出的决策树可以不是唯一的。

4、关于决策树算法:

Hunt 算法

– 信息增益——Information gain （ID3 ）
– 增益比率——Gain ration （C4.5 ）
– 基尼指数——Gini index (SLIQ ，SPRINT)

设 D t 是与结点 t 相关联的训练记录集。

 算法步骤:
– 如果Dt中所有记录都属于同一个类 yt , 则t是叶结点，用yt 标记。
– 如果Dt中包含属于多个类的记录，则选择一个属性测试条件，将记录划分成较小的子集。
  对于测试条件的每个输出，创建一个子结点，并根据测试结果将Dt中的记录分布到子结点中。
  然后，对于每个子结点，递归地调用该算法。

5、决策树构建

Hunt算法采用**贪心策略**构建决策树。

– 在选择划分数据的属性时，采取一系列**局部最优决策**来构造决策树。

决策树归纳的设计问题

– 如何分裂训练记录？

1、怎样为不同类型的属性指定测试条件?
– (4.3.3表示属性测试条件的方法)
2、怎样评估每种测试条件?
– (4.3.4选择最佳划分的度量)

– 如何停止分裂过程？

 当所有的记录属于同一类时，停止分裂；
 当所有的记录都有相同的属性时，停止分裂；
 提前终止树的生长；

6、关于三种著名的决策树

Cart：基本的决策树算法；

Id3：利用增益比较不纯性，停止准则为当所有的记录属于同一类时，停止分裂，或当所有的记录都有相同的属性时，停止分裂；

C4.5：id3的改进版本，也是最流行的分类算法。采用多重分支和剪枝技术。

关于ID3算法：

ID3 使用信息增益作为属性选择度量。
该度量基于香农(Claude Shannon) 在研究消息的值或"信息内容"的信息论方面的先驱工作。
设结点 N 代表或存放数据集D 的元组。

 选择具有最高信息增益的属性作为结点 N 的分裂属性。
 该属性使结果分区中对元组分类所需要的信息量最小，并反映这些分区中的最小随机性或"不纯性" 。
这种方法使得对一个对象分类所需要的期望测试数目最小，并确保找到一棵简单的树。

7、ID3 算法—期望信息/熵 (entropy)

数据集D的 期望信息又称熵 (entropy) ，记作 Info(D)。

计算实例：

熵 (entropy)的性质

 数据集D的不纯度越高，期望信息，即熵 (entropy)的值越大；
 划分所依据的特征越有区分度，划分得到的数据子集D’（结点）越纯；
 即：划分所依据的特征越有区分度，划分得到的数据子集D’（结点）不纯度越小；
 划分所依据的特征越有区分度，划分得到的数据子集D’的熵越小；

8、ID3 算法—划分的期望信息

计算实例：

9、ID3 算法 — 信息增益

信息增益定义为原来的信息需求(仅基于类比例)与新的信息需求(对 A 划分后1)之间的差。

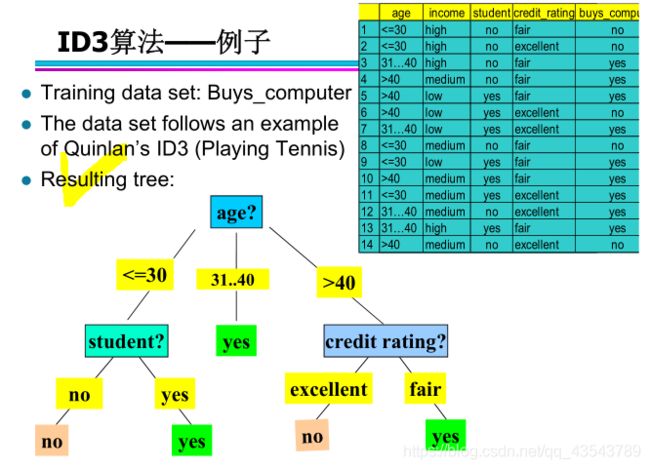
10、ID3 算法—— 例子

ID3 算法求解步骤总结：

1、计算每个属性的信息增益。
2、计算每个属性的期望信息需求。
3、选择在属性中具有最高的信息增益的属性作为分裂属性。

Ending！
更多课程知识学习记录随后再来吧！

就酱，嘎啦！

注：
人生在勤，不索何获。