Resnet网络及其变种
具体阐述一下ResNet网络的细节,你知道的ResNet网络的相关变种有哪些?
1. ResNet解决了什么问题?
首先在了解ResNet之前,我们需要知道目前CNN训练存在两大问题:
- 梯度消失与梯度爆炸:因为很深的网络,选择了不合适的激活函数,在很深的网络中进行梯度反传,梯度在链式法则中就会变成0或者无穷大,导致系统不能收敛。然而梯度弥散/爆炸在很大程度上被合适的激活函数(ReLU)、流弊的网络初始化(Kaiming初始化
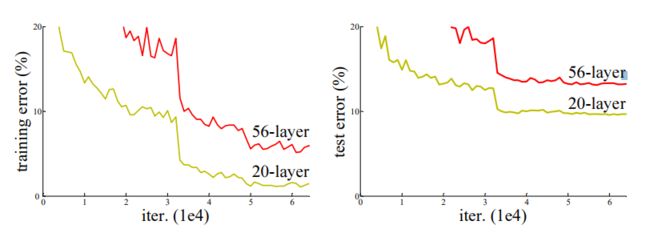
、BN等Tricks)处理了。 - 梯度弥散:当深度开始增加的时候, accuracy经常会达到饱和,然后开始下降,但这并不是由于过拟合引起的。如56-layer的error大于20-layer的error。
ResNet本身是一种拟合残差的结果,让网络学习任务更简单,可以有效地解决梯度弥散的问题。
ResNet网络变种包括ResNet V1、ResNet V2、ResNext`以及Res2Net网络等。
2. ResNet网络结构与其性能优异的原因
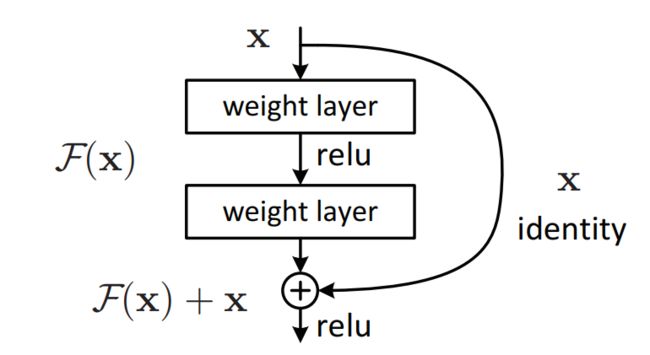
ResNet残差块的结构如图所示。
ResNet网络的优点有:
- 引入跳跃连接,允许数据直接流向任何后续项。
- 引入残差网络,可以使得网络层数非常深,可以达到
1000层以上。
同样,ResNet网络的设计技巧有:
- 理论上较深的模型不应该比和它对应的较浅的模型更差,较深的模型可以理解为是先构建较浅的模型,然后添加很多恒等映射的网络层。
- 实际上我们较深的模型后面添加的不是恒等映射,是一些非线性层,所有网络退化问题可以看成是通过多个非线性层来近似恒等映射是困难的。解决网络退化问题的方法就是让网络学习残差。
通过分析ResNet网络可以知道,ResNet可以被看做许多路径的集合,通过研究ResNet的梯度流表明,网络训练期间只有短路径才会产生梯度流,深的路径不是必须的,通过破坏性试验可以知道,路径之间是相互依赖的,这些路径类似集成模型,其预测准确率平滑地与有效路径的数量有关。
由于ResNet网络中存在很多short cut,所以ResNet又可以被视为很多路径的集合网络。相关实验表明,在ResNet网络训练期间,只有短路径才会产生梯度流动,说明深的路径不是必须的。通过破坏网络中某些short cut实验可以看出,在随机破坏了ResNet网络中的某些short cut后,网络依然可以训练,说明在网络中,即使这些路径是共同训练的,它们也是相互独立,不相互依赖的,可以将这些路径理解为集成模型,这也是理解ResNet网络的性能较好的一个方向。
3. ResNetv2的设计
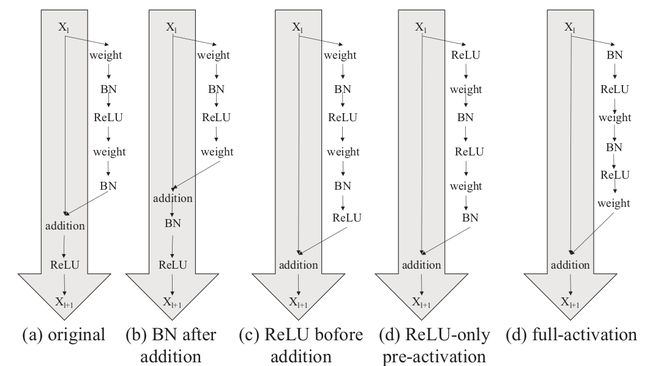
首先,需要看下组对于主干以及分支网络的各种设计:
- (a) 原始 R e s N e t ResNet ResNet模块,[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1sqETZU4-1620617909963)(https://g.yuque.com/gr/latex?f(z)]%3DReLU(z))
- (b) 将 B N BN BN移动到了[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ik7sW3ql-1620617909964)(https://g.yuque.com/gr/latex?addition)]
- © 将 R e L U ReLU ReLU移动到[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TEigc2Qx-1620617909965)(https://g.yuque.com/gr/latex?addition)]。
- (d) 将 R e L U ReLU ReLU移动在残差块之前,[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nG07wvXP-1620617909966)(https://g.yuque.com/gr/latex?f(z)]%3Dz)
- (e) 将 B N BN BN和 R e L U ReLU ReLU移动到残差块之前,[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Il49tRjg-1620617909966)(https://g.yuque.com/gr/latex?f(z)]%3Dz)
在图中, B N BN BN会改变数据的分布, R e L U ReLU ReLU会改变值的大小,上面五个图都是work的,但是第五个图效果最好,具体效果如下:
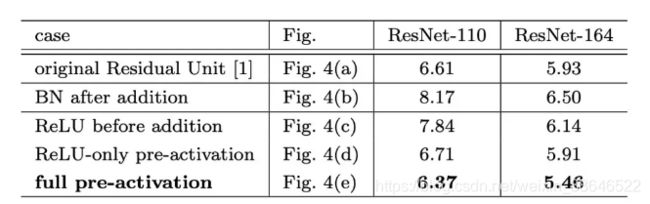
具体效果为什么第五个好呢?先看下面的梯度求导吧!
4. ResNet的梯度公式推导
推导一下ResNet的前向与反向,步骤如下:
我们从上面公式可以看到深层 L L L与浅层 l l l之间的关系;则,假设损失函数为 l o s s loss loss,那么反向传播公式为:
∂ l o s s ∂ x l = ∂ los s ∂ x L ∂ x L ∂ x l = ∂ loss ∂ x L ( 1 + ∂ ∂ x l ∑ i = l L − 1 F ( x i , W i ) ) \frac{\partial l o s s}{\partial x_{l}}=\frac{\partial \operatorname{los} s}{\partial x_{L}} \frac{\partial x_{L}}{\partial x_{l}}=\frac{\partial \operatorname{loss}}{\partial x_{L}}\left(1+\frac{\partial}{\partial x_{l}} \sum_{i=l}^{L-1} F\left(x_{i}, W_{i}\right)\right) ∂xl∂loss=∂xL∂loss∂xl∂xL=∂xL∂loss(1+∂xl∂∑i=lL−1F(xi,Wi))

从上式我们可以看到,ResNet有效得防止了:“当权重很小时,梯度消失的问题”。同时,上式中的优秀特点只有在假设![]() 成立时才有效。所以,ResNet需要尽量保证亮点:
成立时才有效。所以,ResNet需要尽量保证亮点:
- 不要轻易改变identity分支的值。
- addition之后不再接受改变信息分布的层。
因此,在上面五组实验中,第五个(图e)效果最好的原因是:1) 反向传播基本符合假设,信息传递无阻碍;2)BN层作为pre-activation,起到了正则化的作用。
对于图(b),是因为 B N BN BN在addition之后会改变分布,影响传递,出现训练初期误差下降缓慢的问题!
对于图©,是因为这样做导致了 R e s i d u a l Residual Residual的分支的分布为负,影响了模型的表达能力。
对图(d),与图(a)在网络上相当于是等价的,指标也基本相同。
5. 其它相关解释
而除了像是从梯度反传的角度说明 ResNet比较好的解决了梯度弥散的问题,还有一些文章再探讨这些个问题。比如**“The Shattered Gradients Problem: If resnets are the answer, then what is the question?”这篇工作中认为,即使BN过后梯度的模稳定在了正常范围内,但梯度的相关性实际上是随着层数增加持续衰减的**。
而经过证明,ResNet可以有效减少这种相关性的衰减。对于 L L L 层的网络来说,没有残差表示的Plain Net梯度相关性的衰减在 1 2 L \frac{1}{2^{L}} 2L1 ,而ResNet的衰减却只有 1 L \frac{1}{\sqrt{L}} L1 。这也验证了ResNet论文本身的观点,网络训练难度随着层数增长的速度不是线性,而至少是多项式等级的增长
6. 其他变种网络
6.1 WRNS(Wide Residual Networks)
在现有的经验上,网络的设计一般都是往深处设计,作者认为一味的增加深度不是一个有效的方法,residual block的宽度对网络的性能同样很有帮助,所以切入点在每一层的宽度上。
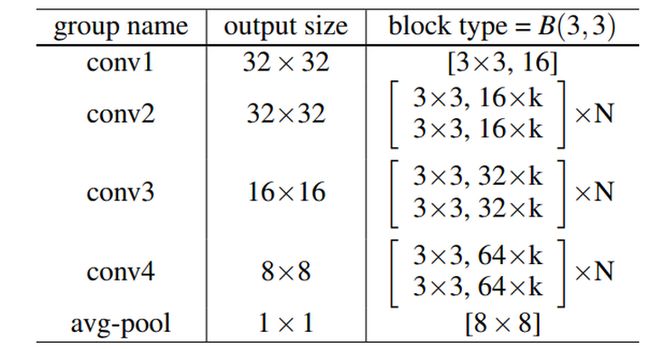
上图为论文中的图,原始的ResNet如图(a)与(b)所示,(b)是使用了bottleneck的residual block,而©与(d)是WRN的结构,主要是通道在原始ResNet通道数上加宽了k倍。
具体参数如下表:
而随着网络深度与宽度的加深,训练参数量过大会导致过拟合,作者提出在residual block里面加入dropout,也是就开头讲到的(d)。
从实验结果看,也能说明,当网络层数depth较浅,或者宽度 k 较小时,网络还不需要加dropout,但是当层数增加,宽度增加,参数量指数增大时,加入dropout可以有效防止model的overfitting。
6.2 ResNext
在ResNet提出deeper可以带来网络性质提高的同时,WideResNet则认为Wider也可以带来深度网络性能的改善。为了打破或deeper,或wider的常规思路,ResNeXt则认为可以引入一个新维度,称之为cardinality。
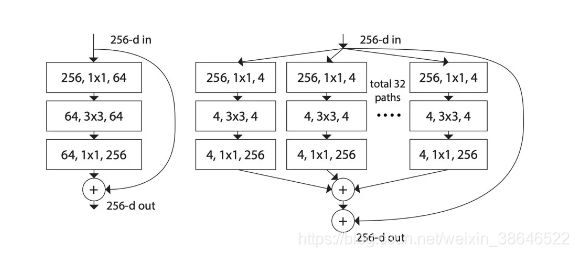
上图中左边为ResNet结构,右边为cardinality=32的ResNeXt结构(也就是含32个group)。其等效结构如下:
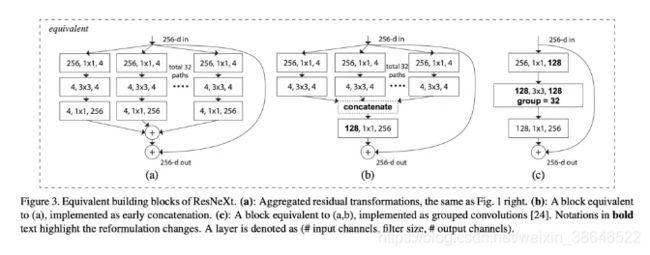
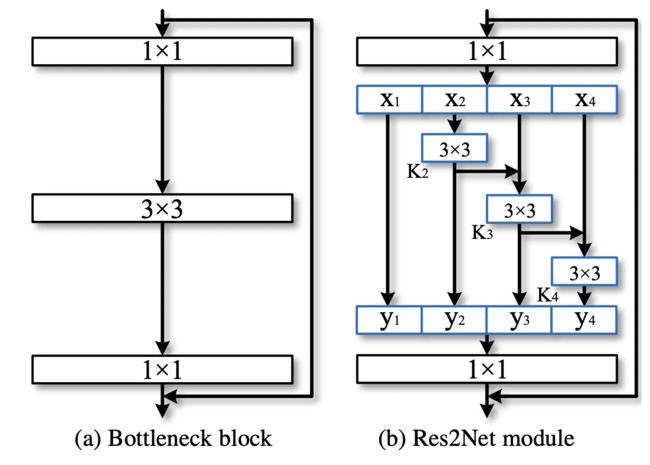
6.3 Res2Net
目前现有的特征提取方法大多都是用分层方式表示多尺度特征。分层方式即要么对每一层使用多个尺度的卷积核进行提特征(如目标检测中的SPPNet),要么就是对每一层提取特征进行融合(如FPN)。
本文提出的Res2Net在原有的残差单元结构中又增加了小的残差块,在更细粒度上,增加了每一层的感受野大小。Res2Net也可以嵌入到不同的特征提取网络中,如ResNet, ResNeXt等等。
在Res2Net中提出了一个新维度叫做scale。Res2Net的结构如下图所示:
上图左边是最基本的卷积模块。右图是针对中间的3x3卷积进行的改进。


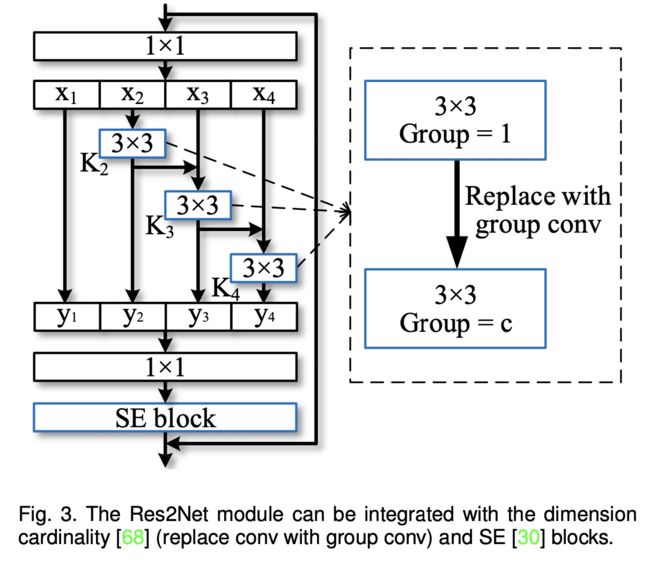
当然,Res2Net可以与像SE模块进行复用。
最后,论文中也给出了关于depth,cardinality以及scale的效果对比,如下图所示:
6.4 ReXNet
作者首先提出了,在传统网络的设计的中可能会存在Representational Bottleneck问题,并且该问题会导致模型性能的降低。其次,通过数学和实验研究探讨网络中出现的Representational Bottleneck问题。
论文中,先给定一个深度为L层的网络,通过 d 0 d_{0} d0维的输入 X 0 ∈ R d 0 × N X_{0} \in R^{d_{0} \times N} X0∈Rd0×N可以得到个被编码为 X L = σ ( W L ( … F 1 ( W 1 X 0 ) ) ) X_{L}=\sigma\left(W_{L}\left(\ldots F_{1}\left(W_{1} X_{0}\right)\right)\right) XL=σ(WL(…F1(W1X0)))的特征,其中 W i ∈ R d i × d i − 1 W_{i} \in R^{d_{i} \times d_{i-1}} Wi∈Rdi×di−1为权重。
这里称 d i > d i − 1 d_{i}>d_{i-1} di>di−1的层为expand层,称 d i < d i − 1 d_{i}
当训练模型的时候,每一次反向传播都会通过输入得到的输出与Label矩阵( T ∈ R d L × N T \in R^{d_{L} \times N} T∈RdL×N)之间的Gap来进行权重更新。

X i = { f i ( W i X ^ i − 1 ) 1 ≤ i < L σ ( W L X ^ L − 1 ) i = L \mathbf{X}_{i}=\left\{\begin{array}{ll} f_{i}\left(\mathbf{W}_{i} \hat{\mathbf{X}}_{i-1}\right) & 1 \leq i
作者抛出了两个问题:
-
Softmax Bottleneck
由上面的卷积公式可以得知,交叉熵损失的输出为 log X L = log σ ( W L X L − 1 ) \log X_{L}=\log \sigma\left(W_{L} X_{L-1}\right) logXL=logσ(WLXL−1),其秩以 W L X L − 1 W_{L} X_{L-1} WLXL−1的秩为界,即 min ( d L , d L − 1 ) \min \left(d_{L}, d_{L-1}\right) min(dL,dL−1)。由于输入维度 d L − 1 d_{L-1} dL−1小于输出维度 d L d_{L} dL,编码后的特征由于秩不足而不能完全表征所有类别。这解释了Softmax层的一个Softmax bottleneck实例。能否通过引入非线性函数来缓解Softmax层的秩不足,性能得到了很大的改善?
-
Representational bottleneck
作者推测,扩展channel大小的层(即层),如下采样块,将有秩不足,并可能有Representational bottleneck。
能否通过扩大权重矩阵的 W i W_{i} Wi秩来缓解中间层的Representational bottleneck问题?
给定某一层生成的第 i i i个特征, X i = f i ( W i X i − 1 ) ∈ R d i × w h N X_{i}=f_{i}\left(W_{i} X_{i-1}\right) \in R^{d_{i} \times w h N} Xi=fi(WiXi−1)∈Rdi×whN, rank ( X i ) \operatorname{rank}\left(X_{i}\right) rank(Xi) 的阈值为 min ( d i , d i − 1 ) \min \left(d_{i}, d_{i-1}\right) min(di,di−1)(假设 N > > d i N>>d_{i} N>>di)。这里 f ( X ) = X ∘ g ( X ) f(X)=X \circ g(X) f(X)=X∘g(X),其中 ∘ \circ ∘表示与另一个函数 g g g的点乘。在满足不等式 rank ( f ( X ) ) ≤ rank ( X ) ⋅ rank ( g ( X ) ) \operatorname{rank}(f(X)) \leq \operatorname{rank}(X) \cdot \operatorname{rank}(g(X)) rank(f(X))≤rank(X)⋅rank(g(X))的条件下,特征的秩范围为:
rank ( X i ) ≤ rank ( W i X i − 1 ) ⋅ rank ( g i ( W i X i − 1 ) ) \operatorname{rank}\left(\mathbf{X}_{i}\right) \leq \operatorname{rank}\left(\mathbf{W}_{i} \mathbf{X}_{i-1}\right) \cdot \operatorname{rank}\left(g_{i}\left(\mathbf{W}_{i} \mathbf{X}_{i-1}\right)\right) rank(Xi)≤rank(WiXi−1)⋅rank(gi(WiXi−1))
因此,可以得出结论,秩范围可以通过增加 ( W i X i − 1 ) \left(W_{i} X_{i-1}\right) (WiXi−1)的秩和用适当的用具有更大秩的函数 g i g_{i} gi来替换展开,如使用 s w i s h swish swish或 E L U ELU ELU激活函数,这与前面提到的非线性的解决方法类似。
当 d i d_{i} di固定时,如果将特征维数 d i − 1 d_{i-1} di−1调整到接近 d i d_{i} di,则上式可以使得秩可以无限接近到特征维数。对于一个由连续的1×1,3×3,1×1卷积组成的bottleneck块,通过考虑bottleneck块的输入和输出通道大小,用上式同样可以展开秩的范围。
针对Layer-Level秩
作者生成一组由单一层组成的随机网络 f ( W X ) f(WX) f(WX):其中 W ∈ R d out × d in , X ∈ R d i n × N W \in R^{d_{\text {out }} \times d_{\text {in }}}, X \in R^{d_{i n} \times N} W∈Rdout ×din ,X∈Rdin×N, d o u t d_{out} dout随机采样, d i n d_{in} din则按比例进行调整,来判断Layer-Level秩。
特征归一化后的秩 ( rank ( f ( W X ) ) / d out ) \left(\operatorname{rank}(f(W X)) / d_{\text {out }}\right) (rank(f(WX))/dout )是由每个网络产生。为了研究 f f f而广泛使用了非线性函数。对于每种标准化Channel大小,作者以通道比例 ( d i n / d o u t ) \left(d_{i n} / d_{o u t}\right) (din/dout)在[0.1, .0]之间 和每个非线性进行10,000个网络的重复实验。图a和b中的标准化秩的展示图。
针对通道配置
随机生成具有expand层(即 d out > d in d_{\text {out }}>d_{\text {in }} dout >din )的L-depth网络,以及使用少量的condense层的设计原则使得 d out = d in d_{\text {out }}=d_{\text {in }} dout =din ,这里使用少量的condense层是因为condense层直接降低了模型容量。在这里作者将expand层数从0改变为 L − 1 L-1 L−1,并随机生成网络。例如,一个expand层数为0的网络,所有层的通道大小都相同(除了stem层的通道大小)。作者对每个随机生成的10,000个网络重复实验,并对归一化秩求平均值。结果如图c和d所示。
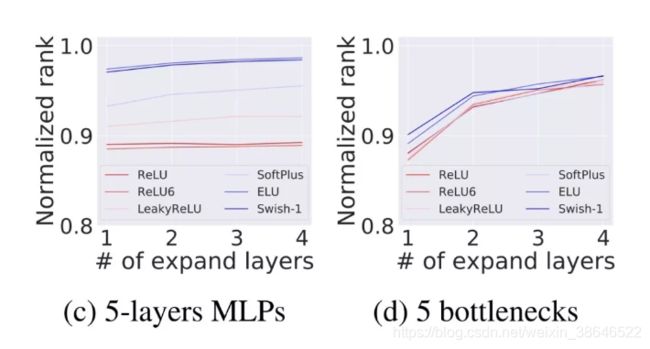
此外,作者测试了采样网络的实际性能,每个配置有不同数量的expand层,有5个bottleneck,stem通道大小为32。数据集用CIFAR100,在表1中给出了5个网络的平均准确率。
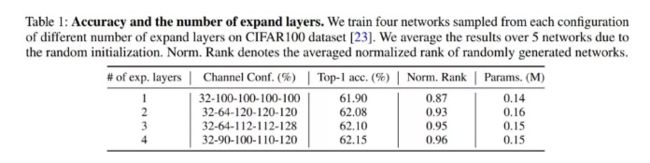
因此,作者这里给出了扩展给定网络秩的设计原则:
- 在一层上扩展输入信道大小;
- 找到一个合适的非线性映射;
- 一个网络应该设计多个expand层。
结论:表征瓶颈(representation bottleneck)将发生在这些扩展层和倒数第2层
解决方案:
- 中间层处理;扩大卷积层的输入通道大小,替换ReLU6s来细化每一层
- 替换ReLU6s来细化每一层;作者扩大了倒数第2层的输入通道大小,并替换了ReLU6
补充
关于ResNet的变种网络,之后再进行变种的其实还有蛮多的,后面我们会说到提高感受野的时候,再进行扩展,如unipose(魔改res2net)等。还有一些如HO-ResNet,结合了数值微分方程相关的,各位感兴趣的可以看看,基本上面试上问到的可能性不大。
大家好,我是灿视。目前是位算法工程师 + 创业者 + 奶爸的时间管理者!
我曾在19,20年联合了各大厂面试官,连续推出两版《百面计算机视觉》,受到了广泛好评,帮助了数百位同学们斩获了BAT等大小厂算法Offer。现在,我们继续出发,持续更新最强算法面经。
我曾经花了4个月,跨专业从双非上岸华五软工硕士,也从不会编程到进入到百度与腾讯实习。
欢迎加我私信,点赞朋友圈,参加朋友圈抽奖活动。如果你想加入<百面计算机视觉交流群>,也可以私我。