基于Matlab的遗传算法优化BP神经网络的算法实现（附算法介绍与代码详解）

目录

一、内容提要

二、算法简介

2.1 遗传算法（Genetic Algorithm，GA）

2.2 BP（Back Propagation）神经网络

三、实例计算

四、代码解读

代码运行

---

代码获取方式详见文末。

一、内容提要

在地学领域中，不同岩性的岩石识别通常是通过人工来实现，但这样比较耗费精力和时间。那我们就来看看机器学习会给岩石图片识别带来怎样的变化。

因此，今天笔者想要分享的是基于遗传算法优化的BP神经网络在岩石图片识别中的应用与代码实现。

首先解释一下为什么要选择基于遗传算法优化的BP神经网络。这是由于BP(Back Propagation)网络总是沿着负梯度的方向下降，导致BP网络很容易陷入局部的极小值，无法得到全局最优解。而遗传算法(Genetic Algorithm, GA)在解决无约束非线性优化问题上性能强大，通常能最大程度逼近全局最优解。

接下来分别简单介绍一下遗传算法和BP神经网络。

二、算法简介

2.1 遗传算法（Genetic Algorithm，GA）

科普中国·科学百科定义：遗传算法是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程 [1]。

遗传算法，简单理解就是通过计算机模拟大自然中的种群在选择压力的进化过程，最终获取某个问题的最优解。

此处分享一个较为生动的例子来帮助大家理解：

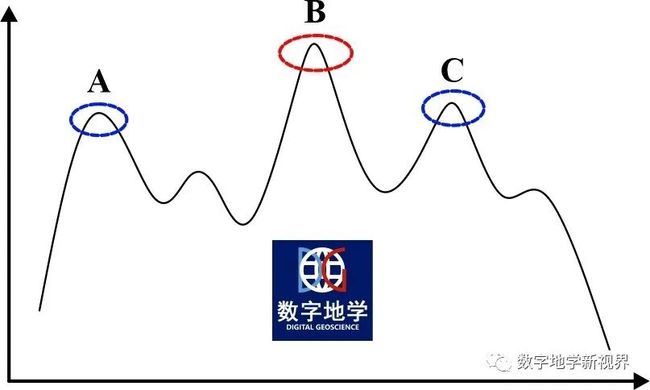
假设有一群小鸟在一片山峰中觅食，只有在最高的山峰上才有最多的食物，越低的位置食物越少、生存环境越恶劣。因此，低海拔山上生存的小鸟活下来的概率越低，而在高峰位置上的小鸟生存下来和继续繁衍后代的概率越高。经过很多年的繁衍和选择后，小鸟们会被归拢到一个个相对较高的山峰上（这个山峰则可以被称为局部最优解，见图1A、C点）。如果小鸟的种群规模足够大，最终则会有种群在最高峰上生存下来，这个点也就是全局最优解（如图1中B点所示）。

图1 山峰示意图

遗传算法的步骤有以下几个关键点：

1. 首先是随机挑选初始种群（随机选择一群小鸟）；

2. 再使用适应度函数对初始种群中的个体打分，并根据个体对环境的适应程度进行选择；（适应度越强，生存能力越高，被选择的概率越大，小鸟在山峰高处适应度越强）

3. 然后从种群中选择两个个体作为父方和母方，抽取父母双方的染色体，进行交叉，并产生后代；

4. 随机选择个体与染色体中的点位进行变异；

5. 重复3、4步骤，直至样本满足条件。

算法流程图参见下面图3左侧。

2.2 BP（Back Propagation）神经网络

科普中国·科学百科定义：BP神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络模型之一[2]。

BP（反向传播）神经网络是一种按误差反向传播训练的多层前馈网络，其简称为BP算法。它的基本思想是基于梯度下降（gradient descent）策略，以目标的负梯度方向对参数进行调整，使网络的实际输出值和期望输出值的误差为最小。

上述表述可能有些晦涩，我们先来理解一下什么是神经网络，简而言之，它一种人工的神经网络，给一个输入（刺激）得到一个输出（反应），而具体得到怎样的输出则取决于我们的神经网络是什么样子的。从数学上来看，要完成这样的一个过程（从输入得到输出）就是找到一个适合的函数来满足从输入到输出的复杂关系。

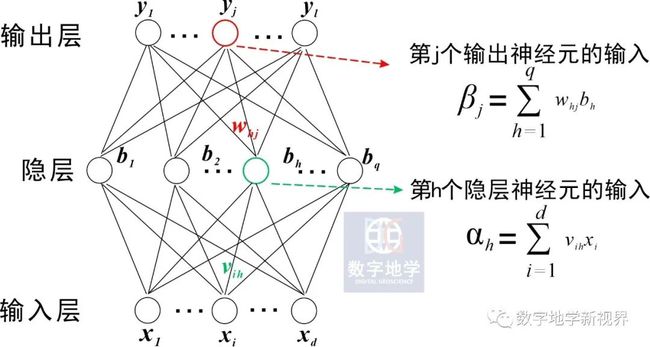
BP神经网络的拓扑结构如图2所示，主要包括输入层、隐层和输出层。可以看到，除了输入层和输出层还包含一个隐层。通俗地讲，人类大脑要会“转弯“才能解决复杂问题，神经网络的隐层设计可以某种精度逼近一个非线性函数，从而得到相对更正确的输出。

图2：BP网络及算法中的变量符号（改自周志华《机器学习》）

BP神经网络的基本思想：学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播过程由输入和权值相乘，经隐层传递（使用激活函数，将线性变换转化为非线性变换）后，再由隐层与权值相乘得到正向输出。这个正向输出结果与预期的输出结果存在一个误差，再从输出通过隐层向输入反传，此误差将修正各层间权值，使误差减小，反复如此达到训练学习的效果（找到了能够表达这个复杂关系的非线性函数）。

BP神经网络的训练过程包括以下几个步骤：

1. 网络初始化。根据拓扑结构的输入输出序列（X,Y）确定网络输入神经元d个、隐层神经元q个，输出层神经元l个，初始化输入层、隐含层和输出层神经元之间的连接权值，初始化隐层阈值γh，输出层阈值θj，给定学习速率（调整权值阈值）和神经元激活函数。

2. 隐层输出计算。根据输入向量X，连接权值vih和阈值γh，计算隐层输出b。

3. 输出层输出计算。根据隐层输出b，连接权值whj和阈值θj，计算BP神经网络预测输出O。

4. 误差计算。根据网络预测输出O和期望输出Y，计算网络预测误差e。

5. 权值更新。根据网络预测误差e更新网络连接权值。

6. 计算全局误差判断算法迭代是否结束，若没有结束，返回步骤2。

而本案例则采用GA与BP共同训练神经网络。

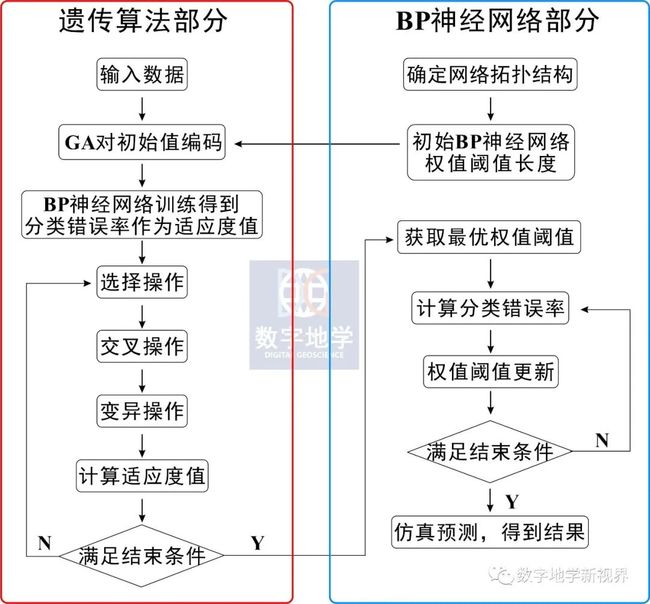
如图3所示，具体流程分为：

（1）BP网络结构的初始化：

确定BP网络输入输出个数，以及神经元个数，以此确定GA中个体的长度。

（2）遗传算法优化：

以BP网络的训练误差作为适应函数，在遗传算法中根据适应度进行种群的选择、交叉、变异操作，找到最优适应度（BP网络误差最小）的个体（最优权值和阈值）。

（3）BP网络接力训练：

BP网络接力训练，保证在全局搜索后，再进行细致的局部搜索。

图3：遗传算法改进BP神经网络算法流程图（错误率即误差）

三、实例计算

实例：基于三种不同岩性的179张岩石样本图片进行岩性分类，部分岩石样本图片如图4所示。

数据：训练集由168个岩石样本图片中心部分像素以及对应岩性组成。选取11个岩石样本图片中心50*50的像素及对应的岩性分类作为测试集，测试建立的模型性能。

目的：构建一个由GA优化结构的BP神经网络模型，用于对新的岩石样本图片进行分类 。

图4：部分岩石样本图片

四、代码解读

代码使用MATLAB自带的模式识别BP网络类patternnet完成神经网络部分，其它部分代码均使用MATLAB的基本语言和函数完成，可以直观给出GA优化结构的BP神经网络模型代码的内部结构和算法细节。

GA-BP的迭代过程主要由以下五个部分完成：

1. fun函数主要计算适应度值，输入个体的网络结构参数，权值和阈值，输出分类的误差，把误差作为个体适应度值。

2. Code函数主要完成个体染色体的随机生成，输入染色体长度、变量取值范围输出染色体的编码值（本代码中使用double编码）。

3. Select函数根据个体适应度大小决定下一代遗传的可能性，使用轮赌法决定该个体是否被复制，如果训练误差小，就可能被多次选中，基因就会在种群中扩散。输入种群变量pop和种群规模sizepop，输出经过复制选择的新种群newpop。

4. Mutation函数用来进行基因突变操作，保证模型的泛化能力。根据种群规模sizepop进行循环，每次循环根据设定好的概率判断是否变异，如果发生变异，则对随机个体的随机单点位进行变异。输入设定好的变异概率pmutation与种群的基本信息，输出经过变异后的新种群newpop。

5. Cross函数用来完成交叉操作，根据种群规模sizepop循环，每次循环根据交叉概率判断是否进行交叉操作，交叉操作为单点交叉，交叉的两个个体与点位都是随机的。输入交叉概率pcorss与种群信息，输出经过交叉操作的新种群newpop。

代码运行

第一步 数据导入

加载训练和测试数据，每个样本为图片对应的采样像素（n×n），每个像素有RGB三种颜色，因此一个样本对应n×n×3个元素。target表示岩性类别1到3，分别使用数组[1, 0, 0]、[0, 1, 0]、[0, 0, 1]表示，因此有3列。DataSet.mat包含四个变量分别是：testTarget (11×3)、testXData (11行，n×n×3列)、trainTarget (168×3)、trainXData (168行，n×n×3列) 。

load DataSet.mat

第二步 网络结构初始化

% 定义输入元素个数，输出元素格式，和隐层神经元个数
inputNum = size(trainXData,2); 
hiddenNum = 21;
outputNum = size(trainTarget,2);

% 给定训练函数
trainFcn = 'trainscg';

预先训练一次网络，这样可以将网络每一层的参数个数自动进行赋值，否则会有未知bug。

% 构建网络，并初始化网络结构
netPatR=patternnet(hiddenNum, trainFcn);
[netPatR,tr] = train(netPatR,input_train,output_train);

第三步 遗传算法的参数初始化与种群初始化

参数初始化

maxgen=10;                 %进化代数，即迭代次数
sizepop=10;                %种群规模
pcross=[0.2];              %交叉概率选择，0和1之间
pmutation=[0.1];           %变异概率选择，0和1之间

种群初始化

%随机产生一个种群
individuals.chrom(i,:)=Code(lengthChrom,bound); 

第四步 循环内遗传算法的选择、交叉、变异和适应度计算

选择

individuals=Select(individuals,sizepop);

交叉

individuals.chrom=Cross(pcross,lengthChrom,individuals.chrom,sizepop,bound);

变异

individuals.chrom = Mutation(pmutation, lengthChrom, individuals.chrom, sizepop, i, maxgen, bound);

计算适应度

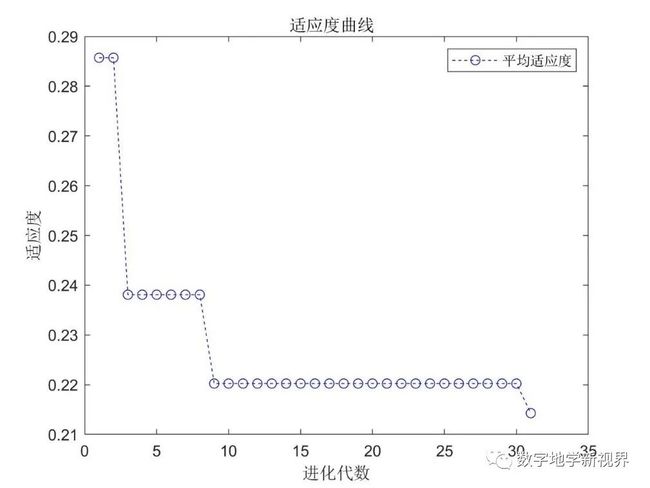
individuals.fitness(j)=fun(x,inputNum,hiddenNum,outputNum,netPatR,inputn,outputn);

输出适应度曲线

图5：适应度（这里指误差）与进化代数关系图

第五步 将GA迭代出的最优结构赋值给BP网络，并使用BP网络接力训练

用遗传算法优化的BP网络进行值预测

netPatR.iw{1,1}=reshape(w1,hiddenNum,inputNum);
netPatR.lw{2,1}=reshape(w2,outputNum,hiddenNum);
netPatR.b{1}=reshape(B1,hiddenNum,1);
netPatR.b{2}=B2';

网络训练

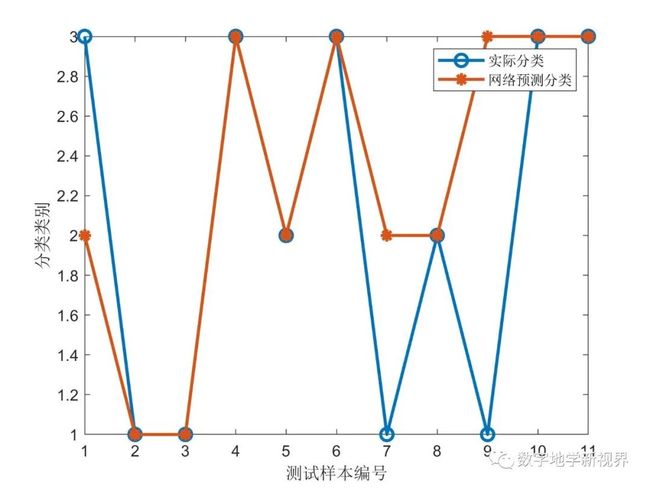
[netPatR,per2]=train(netPatR,inputn,outputn);

最终对测试集中的11个样本进行分类结果如图6所示：

图6：训练效果图

参考文献

[1] 郑树泉．工业智能技术与应用[M]．上海：上海科学技术出版社，2019：250-251

[2] 闻新，张兴旺，朱亚萍，李新著．智能故障诊断技术：MATLAB应用：北京航空航天大学出版社，2015.09

【注】此文章版权归数字地学新视界账号所有，如需转载务必联系后台管理员。否则将维权到底。

---

重点重点重点！！！

关注公众号并联系数字地学新视界微信后台管理员，可领取完整版带有详尽注释的示例代码！

[如何获取管理员联系方式]：菜单栏中的联系我们——>转载须知，添加即可。

知识创作分享不易，希望与大家共同成长进步~ 

【多见多闻】| 基于遗传算法优化的BP神经网络在岩石图片识别中的应用与代码实现 (qq.com)https://mp.weixin.qq.com/s?__biz=Mzg5MTcyODU4OQ==&mid=2247483775&idx=1&sn=bf2ce6427e693dec437f99d2f2bbae74&chksm=cfc9a6ddf8be2fcb507abfd002017b55081d03b8adb96178d86c0cad6e4879f14659340268f2&token=552115172&lang=zh_CN#rd

---